一种改进的杂波率未知环境下GM-CPHD滤波算法*
2019-12-26王杰贵朱克凡
彭 聪,王杰贵,朱克凡
(1 国防科技大学电子对抗学院, 合肥 230037; 2 电子对抗信息处理重点实验室, 合肥 230037)
0 引言
随机有限集(RFS)框架下的多目标跟踪方法[1]是近年来解决多目标跟踪问题的一个研究热点,这类算法避免了传统的多目标跟踪算法中的数据关联环节,解决了数据关联带来的“组合爆炸”问题[2]。由于RFS框架下的积分为集值积分,通常无法求解,因此近似的滤波方法被提出,例如基于一阶统计矩近似的概率假设密度(probability hypothesized density,PHD)滤波算法[3]和基于一阶统计矩和势近似的势概率假设密度(cardinalized PHD,CPHD)滤波算法[4]。
Mahler在文献[3]中给出了PHD滤波器的递推方程。由于PHD滤波算法是对多目标密度的一阶矩近似,未考虑高阶信息,导致了在低信噪比环境下对目标数目估计不稳定;另一方面,PHD滤波器只用一个参数来传播目标的势信息,并且利用泊松分布来近似未知的势分布,因为泊松分布的均值和协方差是相等的,所以当目标数目较大时,PHD滤波器的目标估计的协方差将相应变大[5]。针对以上问题,Mahler在文献[4]中提出了CPHD滤波算法,该算法在传播多目标强度函数的同时传播多目标的势分布信息,因此CPHD滤波器对于目标数目有一个更精准的估计,并且在假设条件中,放宽了目标数均值服从泊松分布的要求,使算法的适用范围更广。
然而传统的CPHD滤波算法需要已知杂波的先验知识,当杂波的信息和假设条件不符时,会严重影响目标跟踪的精度。在现实情况中,杂波的信息通常是未知的,针对杂波先验信息未知情况下的CPHD滤波跟踪,众多学者进行了大量研究。文献[6]中提出了一种杂波率未知的CPHD滤波算法,但仍需假设杂波分布情况;针对这一问题,文献[7]在杂波分布服从无限混合模型的前提下,采用狄利克雷过程混合模型(DPMM)的非参数聚类得到杂波模型,进而对杂波的空间分布进行估计;文献[8]在量测似然函数的基础上增加了目标数目的估计,提升了CPHD滤波器目标数目的估计精确度;文献[9]对目标和杂波分别独立建模,采用最优高斯估计对目标强度进行预测,实现了未知杂波环境下多机动目标的跟踪。上述算法在杂波先验信息未知情况下均能实现多目标的跟踪,但算法的计算复杂度较高,为O(nm3),n为目标数,m为观测数。
针对杂波率未知环境下的CPHD滤波跟踪问题,文中做了以下工作:首先提出了杂波率未知环境下的CPHD滤波算法,然后针对算法中计算量过大的问题,引入最大似然自适应门限,利用门限内的量测进行CPHD滤波算法的更新步骤,从而降低计算复杂度。
1 CPHD滤波算法
CPHD滤波算法是在以下假设条件下进行的:
1)目标的运动状态和其生成的量测相互独立;
2)新生目标的RFS是独立同分布的,并且与存活目标的RFS相互独立;
3)杂波的RFS是独立同分布的,且与目标量测集相互独立;
4)预测和后验的多目标RFS均近似为独立同分布的。
基于以上假设条件,Mahler在文献[4]中给出了CPHD的数学推导:
①预测步
假设k-1时刻的后验强度为vk-1,后验势分布为ρk-1,则预测强度vk|k-1和预测的势分布ρk|k-1可以表示如下:
(1)
(2)
式中:
(3)
式中:pS,k(ζ)表示k时刻目标的生存概率;fk|k-1(·|ζ)为k时刻单目标的概率转移密度函数;γk(·)是k时刻新生目标的强度;ρΓ,k(·)表示k时刻新生目标的势分布[10]。
②更新步
假设k时刻的预测强度表示为vk|k-1,预测势分布表示为ρk|k-1,则更新的目标强度vk和势分布ρk表示如下:
(4)
(5)
式中:
(6)
(7)
Λk(v,Z)={〈v,ψk,z〉∶z∈Zk}
(8)
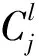
2 改进的GM-CPHD滤波算法
2.1 杂波率未知环境下的GM-CPHD滤波算法
(9)
k-1时刻真实目标的后验强度函数为:
(10)
(11)
(12)
(13)
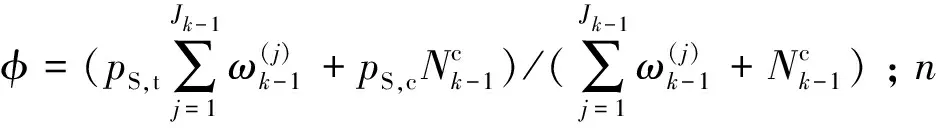
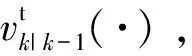
(14)
则更新的目标强度函数,杂波期望数目和混合势分布各自表示如下:
(15)
(16)
(17)
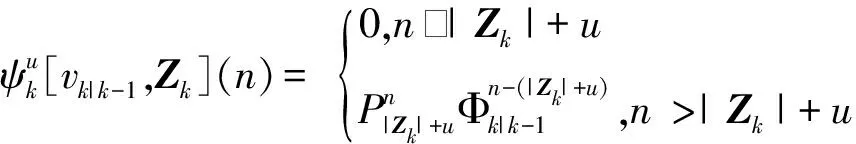
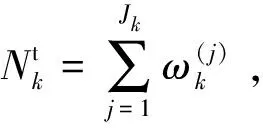
2.2 最大似然自适应门限
上述2.1节中给出了杂波率未知条件下的GM-CPHD滤波器实现方法,通过对真实目标和杂波分别独立建模,单独传播两种目标类型的强度函数,杂波的期望数以及混合势分布,实现杂波率未知情况下的CPHD滤波算法。但是CPHD算法本身计算量巨大,即便是具有封闭形式解的高斯混合实现方法,计算复杂度仍然达到了O(nm3),n为目标数,m为观测数。在杂波较为密集的环境下,算法运行时间过长,缺乏实时性。针对这个问题,本节采用最大似然门限对观测值进行处理,利用通过门限的量测值进行算法更新步,从而减小算法计算量,达到提高算法实时性的效果。
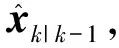
(18)
其残差协方差矩阵为:
(19)
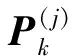
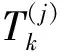
(20)
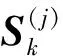
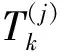
(21)

2.3 改进的算法流程
提出的改进的未知杂波率条件下的GM-CPHD滤波算法流程总结如下:
1)对真实目标的随机有限集和杂波的随机有限集分别进行独立建模;
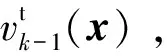
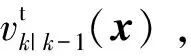
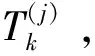
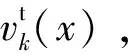
6)对高斯项进行修剪合并,提取目标的状态信息,详细步骤可参考文献[12]。
3 仿真实验与分析
在本次仿真实验中,共有6个做线性运动的目标,目标轨迹图如图1(a)所示。进行100次蒙特卡洛仿真,仿真中将杂波率已知的GM-CPHD(KC-GM-CPHD),杂波率未知的GM-CPHD(UC-GM-CPHD)和文中提出的改进的杂波率未知的GM-CPHD(IUC-GM-CPHD)进行对比实验,以验证算法的可行性与优势。
3.1 仿真场景设置
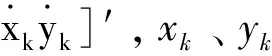
(22)
式中:F表示系统的状态转移矩阵,过程噪声是均值为0,协方差为σw=10的高斯白噪声。
量测方程为:
(23)
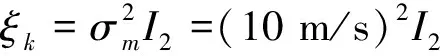
真实目标的存活率pS,t=1,目标的检测率pD,t=0.98,新生目标强度表示为:
(24)

3.2 仿真结果分析
图1(a)显示了目标的运动轨迹图,共有6个目标做线性运动,目标1和目标5起始于t=1 s,消亡于t=70 s;目标2和目标3起始于t=40 s,消失于t=100 s;目标4起始于t=60 s,消亡于t=100 s;目标6起始于t=1 s,消亡于t=100 s。图1(b)显示的是x轴和y轴的目标与杂波态势图。
图2是3种算法对目标数目估计的仿真图,图2(a)、图2(b)、图2(c)分别为KC-GM-CPHD算法、UC-GM-CPHD算法和IUC-GM-CPHD算法对目标个数的估计图。从图中可以看到,在k=7 s,25 s,39 s,40 s,47 s,58 s,59 s,…等12个时刻,KC-GM-CPHD算法对目标数目估计出现了偏差;在k=15 s,18 s,25 s,26 s,33 s,39~41 s,…等18个时刻,UC-GM-CPHD算法对目标个数估计出现了误差;在k=14 s,18 s,19 s,28 s,32 s,33 s,38 s,39 s,…等16个时刻,文中提出的IUC-GM-CPHD算法对目标数估计出现了误差。对比来看,KC-GM-CPHD算法对目标数的估计更准确,这是因为该算法中杂波先验信息已知,而不是在滤波过程中估计得到,因此对目标数的估计更为准确,但3种算法在目标估计偏差上总体相近,在失去杂波先验知识的情况下,UC-GM-CPHD算法和IUC-GM-CPHD算法对目标数的估计偏差在可接受范围。
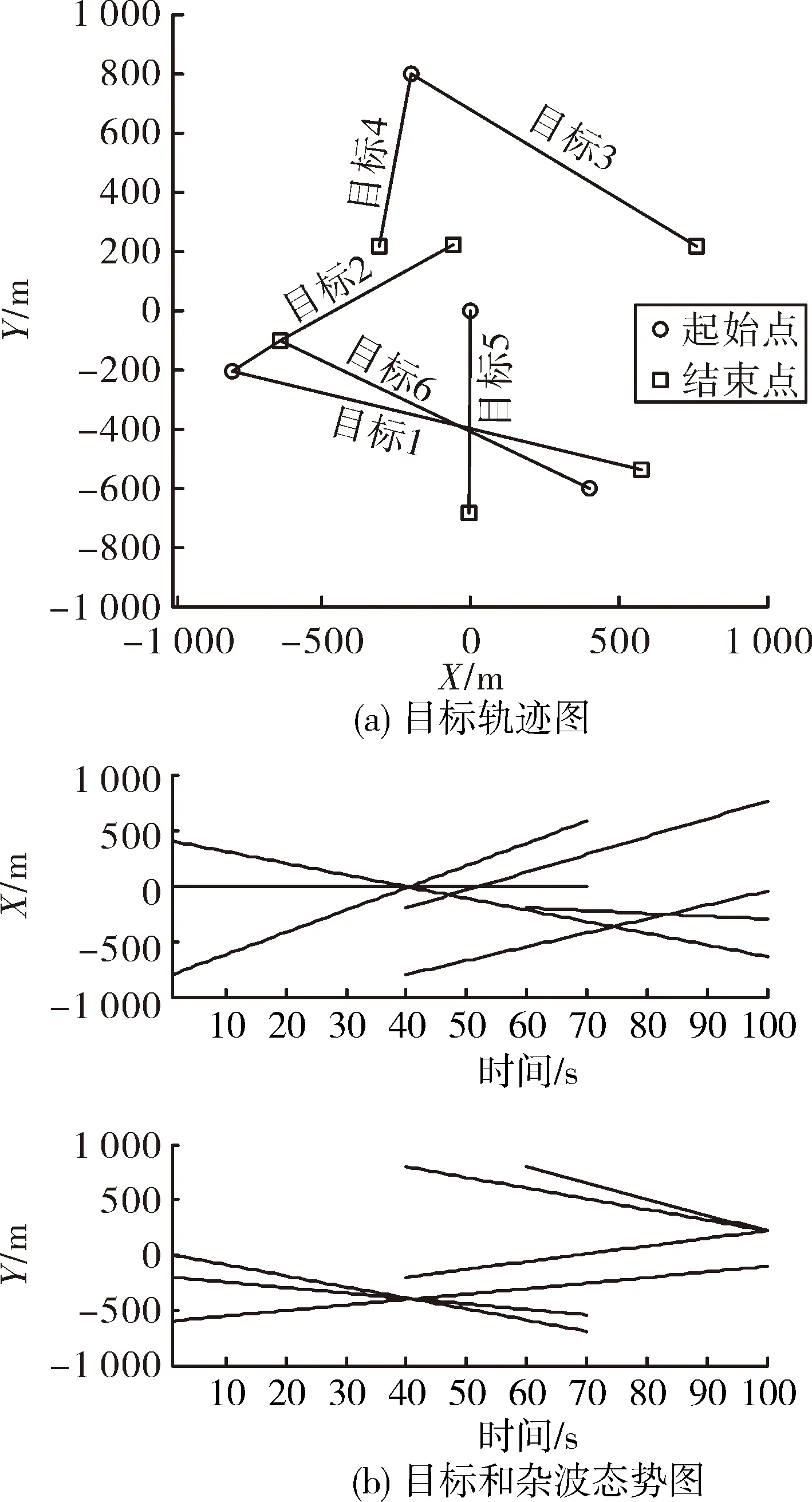
图1 目标轨迹和杂波态势图
引入最优子模式指派(OSPA)距离[13]来评价算法跟踪性能的优劣,它是衡量两个集合间差异度的误差距离。图3给出了3种算法的OSPA距离对比图,可以看到,蓝色虚线代表的KC-GM-CPHD算法相较于红色点划线代表的UC-GM-CPHD算法与黑色实线所代表的IUC-GM-CPHD算法来说,波动次数较少,跟踪性能略优。但是曲线的整体变化趋势相近,只是在某些时间点,未知杂波背景下的算法跟踪误差要比已知杂波背景下的跟踪误差略大。从OSPA距离对比图可以看出,相较于杂波率已知的KC-GM-CPHD算法,尽管未知杂波率情况下所能利用的环境信息较少,使得杂波率未知的UC-GM-CPHD算法和IUC-GM-CPHD算法在跟踪精度上有一定的损失,但仍能够准确的进行目标跟踪。
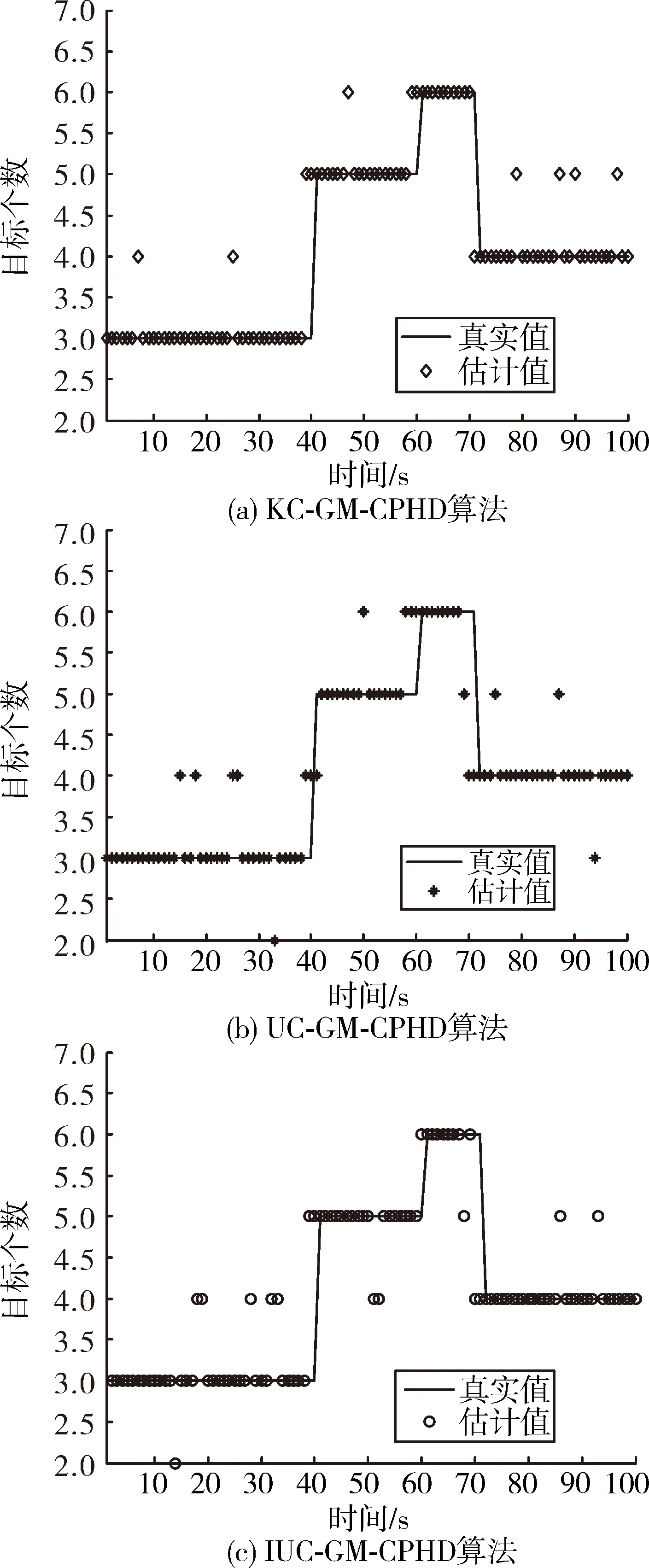
图2 3种算法对目标数目的估计图
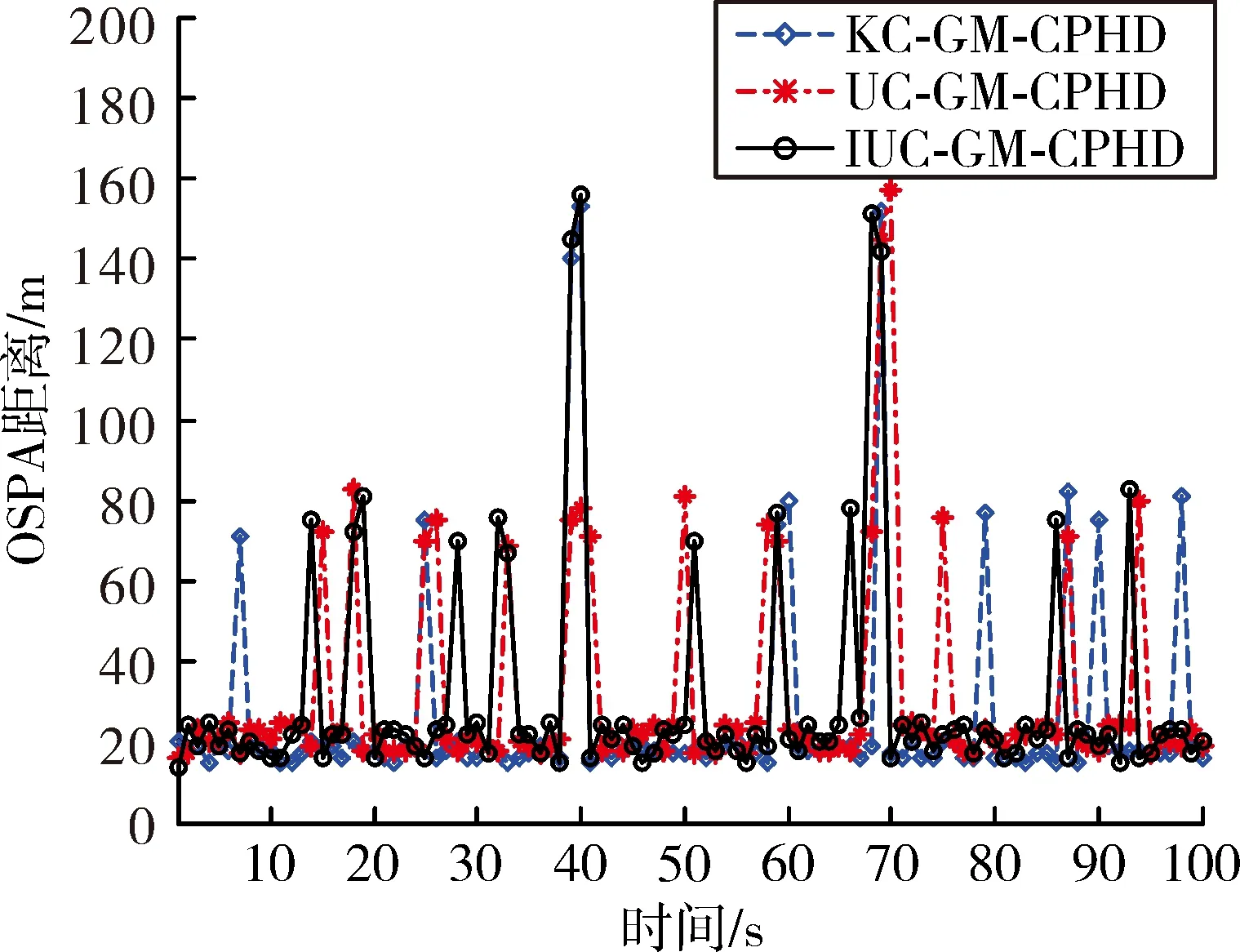
图3 OSPA距离对比图
图4是所提算法的杂波期望个数估计图,在起始阶段和有新生目标产生的时刻,杂波期望个数估计会出现相对较大的波动,这是因为算法将部分新生目标的量测归为杂波所致。可以看到,在杂波率未知的环境下,算法不仅能够对多个目标进行跟踪,还能估计出各个时刻的杂波期望个数。
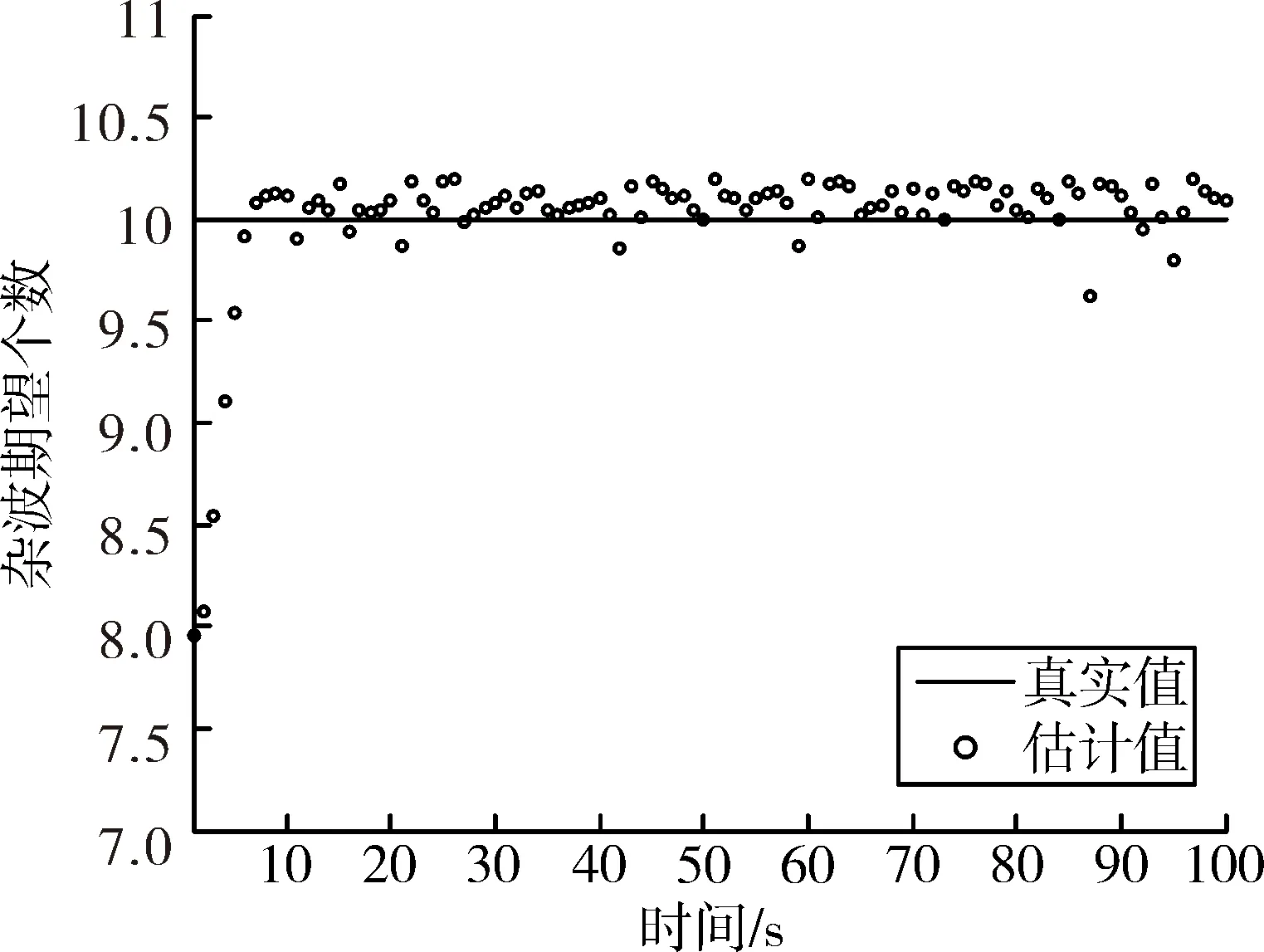
图4 杂波期望个数估计
表1给出了文中算法与KC-GM-CPHD算法、UC-GM-CPHD算法进行一次蒙特卡洛仿真的平均时间对比图。由于传统的GM-CPHD的计算复杂度与观测数的3次方成正比,因此算法的运行时间较长,尤其在杂波较多的环境下,计算复杂程度将急剧增加,影响算法的跟踪性能。从表1中可以看出,提出的IUC-GM-CPHD算法在运行时间上远小于另外两种算法,这是由于算法进行滤波更新时所用的量测数据经过了最大似然自适应门限处理,大大减少了无效量测进入算法更新步,从而使运行时间大幅度减小。

表1 平均运行时间对比图
4 结束语
针对传统的CPHD滤波算法在杂波率未知条件下无法对目标进行跟踪,且计算量繁重的问题,提出了一种改进的未知杂波率环境下的CPHD滤波算法,实现了未知杂波率环境下的目标跟踪,并将算法运行时间大幅减少。虽然跟踪精度上有一定的损失,但仍能够准确的进行多目标的跟踪。如何进一步提升算法的跟踪精度,是下一步研究的重点。
