基于正负线性调频信号的压缩感知波形分离方法*

陈 桥,童宁宁,丁珊珊,胡仁荣

(空军工程大学防空反导学院, 西安 710051)

0 引言

传统的MIMO雷达在接收端放置一组与发射波形相匹配的滤波器组实现对回波中不同波形分量的分离。但发射的正交波形信号无法保证完全正交,从而匹配滤波输出存在严重的互耦噪声,大大影响了距离向分辨性能。

基于压缩感知(compressive sensing,CS)的MIMO雷达波形分离方法,能够显著提高波形分离的效果。利用DOD和DOA估计信息,实现收发通道包络对齐；基于目标一维距离像稀疏性,构建感知矩阵,利用联合稀疏恢复算法实现多接收通道回波的波形分离。

文献[1]已经证明了压缩感知算法的重构效果与匹配字典的最大相关系数之间存在关联。而基于压缩感知的波形分离方法的感知矩阵是由发射波形及其时延构成,因此感知矩阵的列相关特性取决于信号的相关特性。文中对相位编码信号、OFDM-chirp信号和正负线性调频信号的相关性能进行分析,选择了低自相关旁瓣和低互相关电平的正负线性调频波形作为发射波形使波形分离效果最优。

1 MIMO雷达CS波形分离方法

1.1 MIMO雷达信号模型

平面阵列发射一组相位编码信号,其中第m个发射信号(基频)形式为：

φm(t)=exp{jφm(t)}

(1)

式中：m=0,1,2,···,M2-1,t为快时间,φm(t)为相位编码函数。

考虑一个包含U个强散射中心的目标,假定O为目标上的一个参考点,目标位于斜视条件下。设目标上第q个散射点Q与第m个发射阵元Tm的距离为TmQ,和第n个接收阵元Rn的距离为RnQ。单次快拍条件下目标可认为相对雷达静止,所以去掉载频之后,第n个接收阵元接收到的目标回波信号可表示为：

(2)

式中：n=0,1,···,N2-1,c为波速,λ为波长,σq为散射点Q的散射系数。

1.2 CS波形分离方法

包络对齐后的回波可以表示为：

(3)

式中：

τq,mn=(TmQ+RnQ-TmO-RnO)/c

则式(3)可简化为:

(4)

对距离向成像区域进行离散化,设位于第k个距离单元的所有散射点构成集合{q|τq,mn=τk},则式(4)可表示为:

(5)

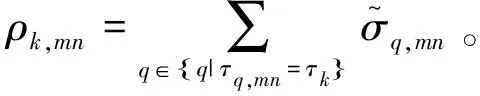
y=Φθ

(6)

式中:y∈CI×1为yn(t)的向量形式,I距离向采样数量；

(7)

ρ·m=[ρ1,mn,…,ρk,mn,…,ρK,mn]∈CK×1

(8)

Φ=[Φ0,…,Φm,…,ΦM2-1]∈CI×M2K

(9)

Φm=[φm(τ1),…,φm(τk),…,φm(τk)t]∈C1×K

(10)

式中：φm(τk)∈CI×1为φm(t-τk)的向量形式。

利用CS重构算法求解式(6)中的未知向量θ,即可实现不同发射波形的分离。其中ρ.m对应了第m个发射波形的一维距离像。待所有接收阵元回波信号进行CS分离后,按照等效阵元位置对分离结果进行重新排列可以二维成像。相对于传统的匹配滤波分离方法,CS重构算法具有很好的旁瓣抑制效果,能够有效抑制非正交波形的互耦噪声

1.3 实例仿真

MIMO雷达采用一个2发20收的均匀线阵。发射波形采用文献[2]中的2个40码元4相相位编码信号,采用一个由11个散射点构成的多散射点目标。

图1、图2分别为第1个PCM发射信号和第2个PCM发射信号对应的分离结果。可以看到,对于多散射点目标,匹配滤波波形分离效果很差,而压缩感知方法仍能实现不同波形分量的有效分离。

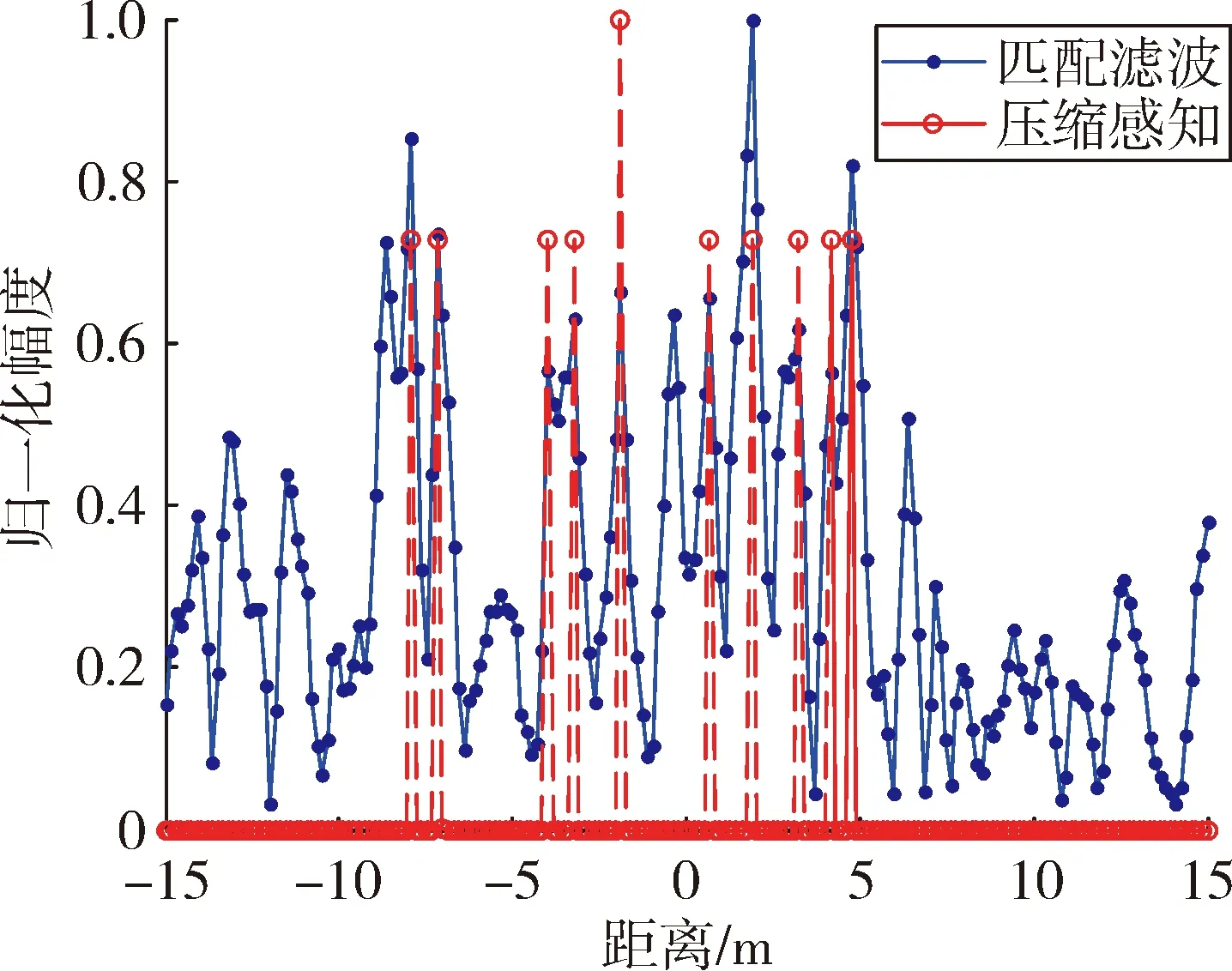
图1 第1个PCM发射信号分离结果

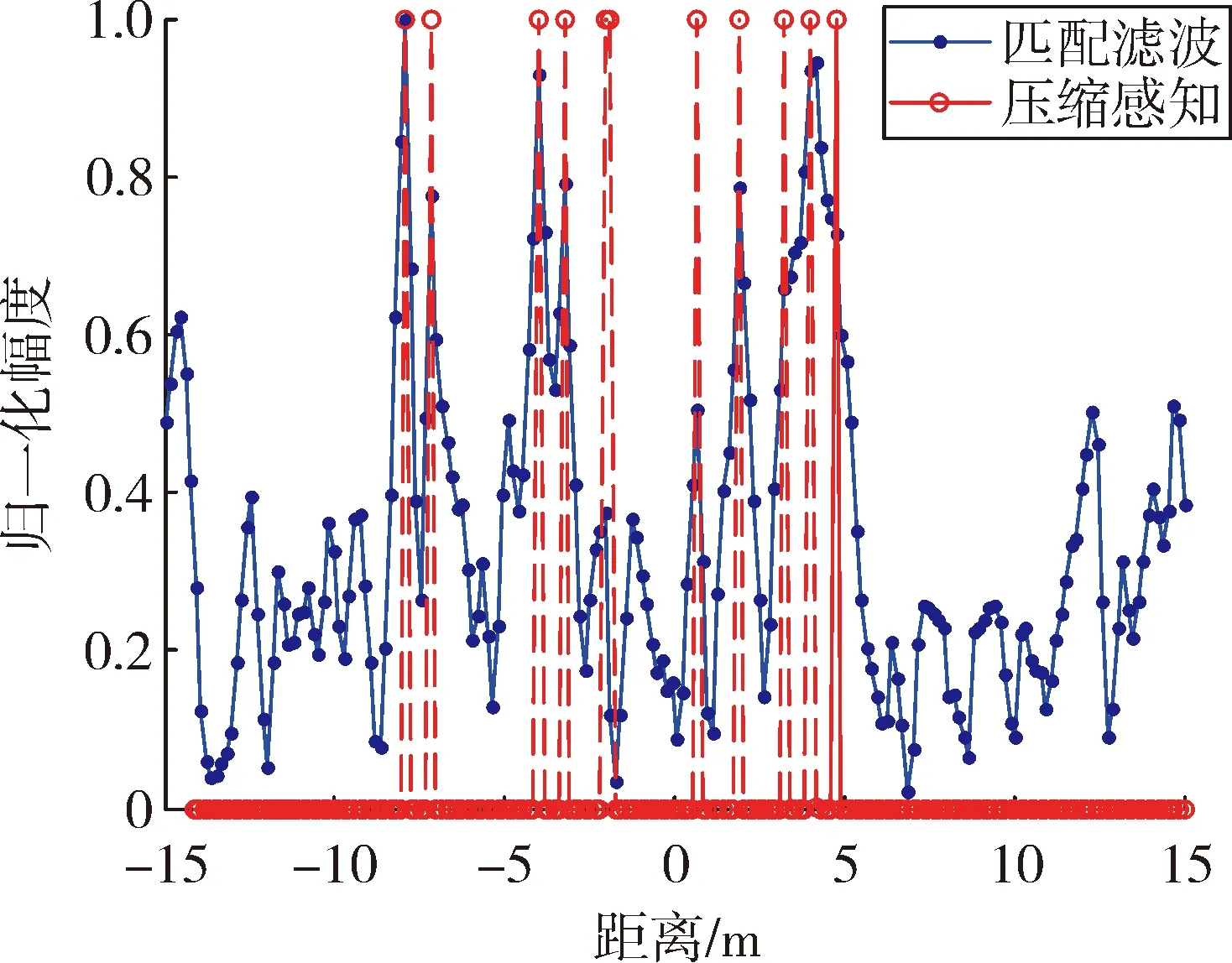
图2 第2个PCM发射信号分离结果

2 信号波形性能分析

压缩感知重构效果的好坏由匹配字典中的最大相关系数所决定。最大相关系数越小,重构效果越好。将压缩感知的理念用于波形分离时,由式(9)、式(10)可知该方法的感知矩阵是由发射波形及其时延构成的,感知矩阵的每一列都是延时了一定时间的发射信号。最大相关系数越小,对应于发射波形具有低自相关旁瓣和低互相关电平。通过上面的分析,选择具有低自相关旁瓣和低互相关电平的发射波形(匹配字典的最大相关系数较小),可以得到较好的成像质量。

2.1 相位编码波形相关性能

M组NPCM位的相位编码正交信号中第m个相位编码信号表达式为:

sm(t)=φm(t)·exp(j2πf0t),m=1,2,…,M

(11)

式中：f0表示信号的载频,φm(t)表示复包络。

(12)

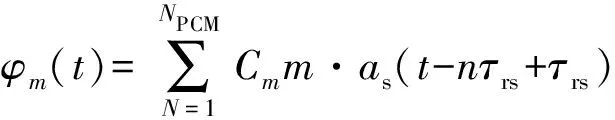
选用文献[2]中4个4项40码的相位编码信号对其自相关函数和互相关函数进行仿真。

图3 相位编码信号的相关性

2.2 OFDM-chirp信号相关性能

正交频分多路复用信号波形已被广泛应用于MIMO通信系统中[7],它在保证各个波形可分的同时克服多径干扰。在MIMO阵列中,设发射阵元发射的线性调频脉冲信号si(t),i=1,2,···,M,M为发射阵元数,那么

(13)

当设定雷达载波频率10 GHz,雷达工作波长0.03 m,雷达采样频率400 MHz,脉冲宽2 μs,带宽为200 MHz 时,OFDM-chirp信号的相关性见图4。

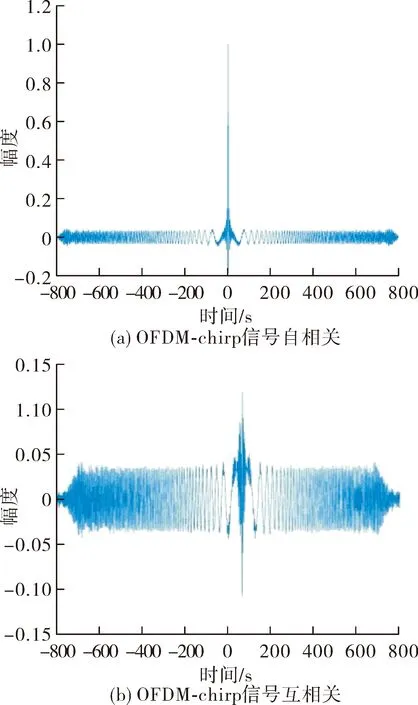
图4 OFDM-chirp信号的相关性

2.3 正负线性调频信号相关性能

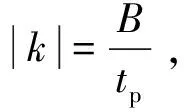
(14)

该信号的包络表达式是：

(15)

式中:

选取的4个发射信号是正负线性调频信号,负正线性调频信号,正线性调频信号,负线性调频信号。

(16)

为了方便比较,设正负线性调频信号的带宽与OFDM-chirp信号的相同,其自相关与互相关如图5所示。

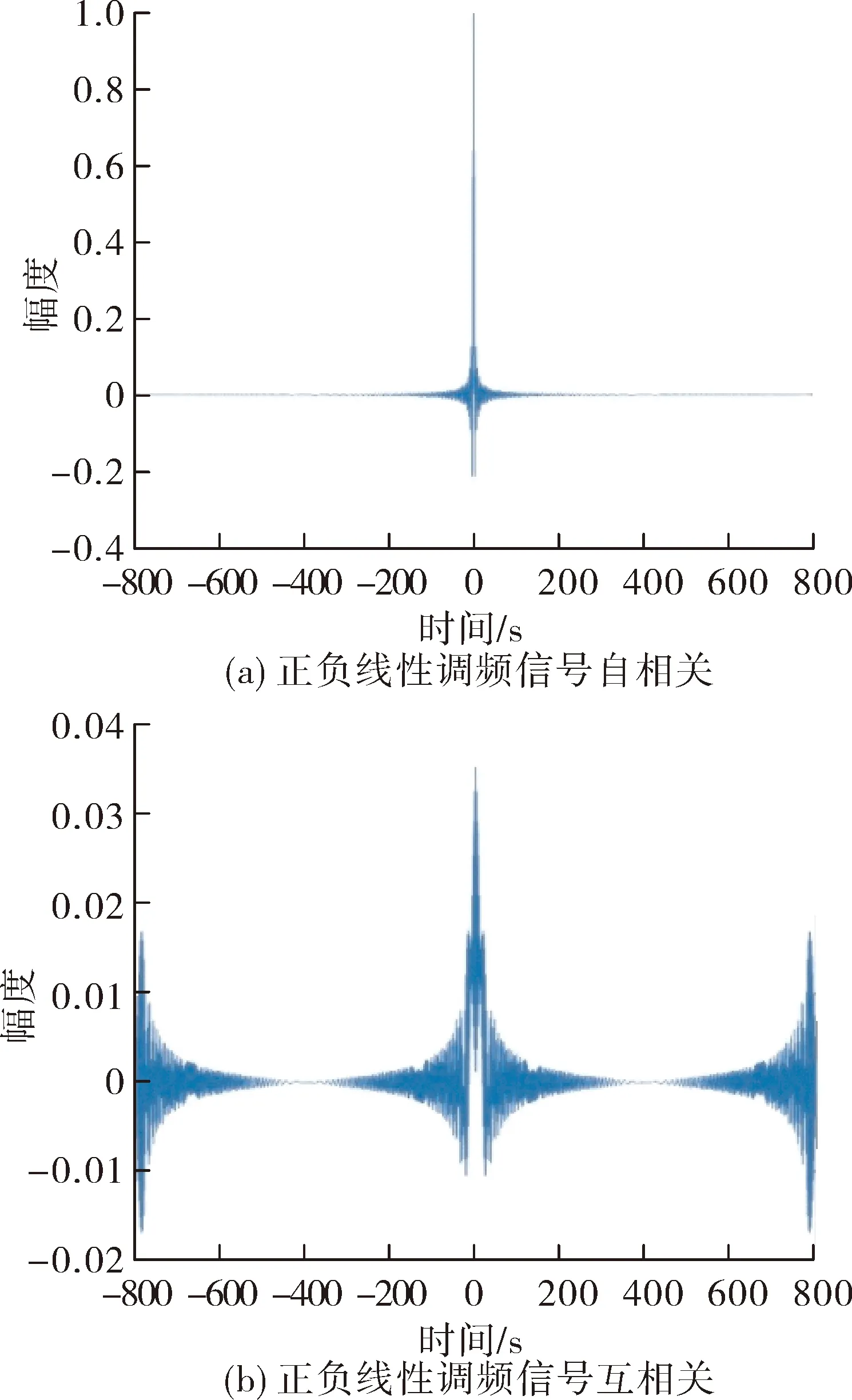
图5 正负线性调频信号的相关性

3 成像效果仿真分析

仿真条件：MIMO雷达阵列采用M=4,N=20,阵元间隔d=6 m。成像目标选取YakPlane模型。稀疏重构算法统一采用联合稀疏恢复算法MFOCUSS[6]。

仿真一：相位编码信号应用于波形分离并成像,图6(a)表示用传统的匹配滤波实现波形分离时的呈现效果,而图6(b)则是采用压缩感知波形分离方法的效果。

图6 波形分离并成像效果

由图可以看出CS恢复算法直接重构不同波形分量对应的目标一维距离像,有效抑制了波形非正交带来的距离向高旁瓣,大大改善了分离效果。

仿真二：波形采用OFDM-chirp信号的成像效果如图7所示。

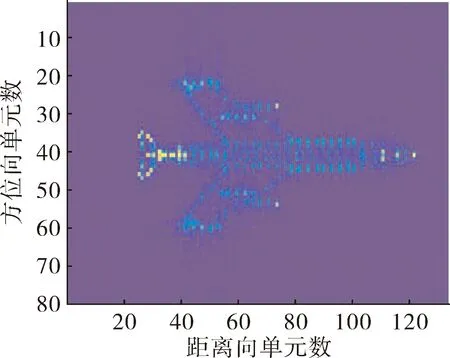
图7 OFDM-chirp信号CS波形分离并成像

由图7可以看出相比于相位编码信号OFDM-chirp信号具有更好的成像效果。

仿真三：正负线性调频信号应用于压缩感知波形分离的成像效果如图8所示。

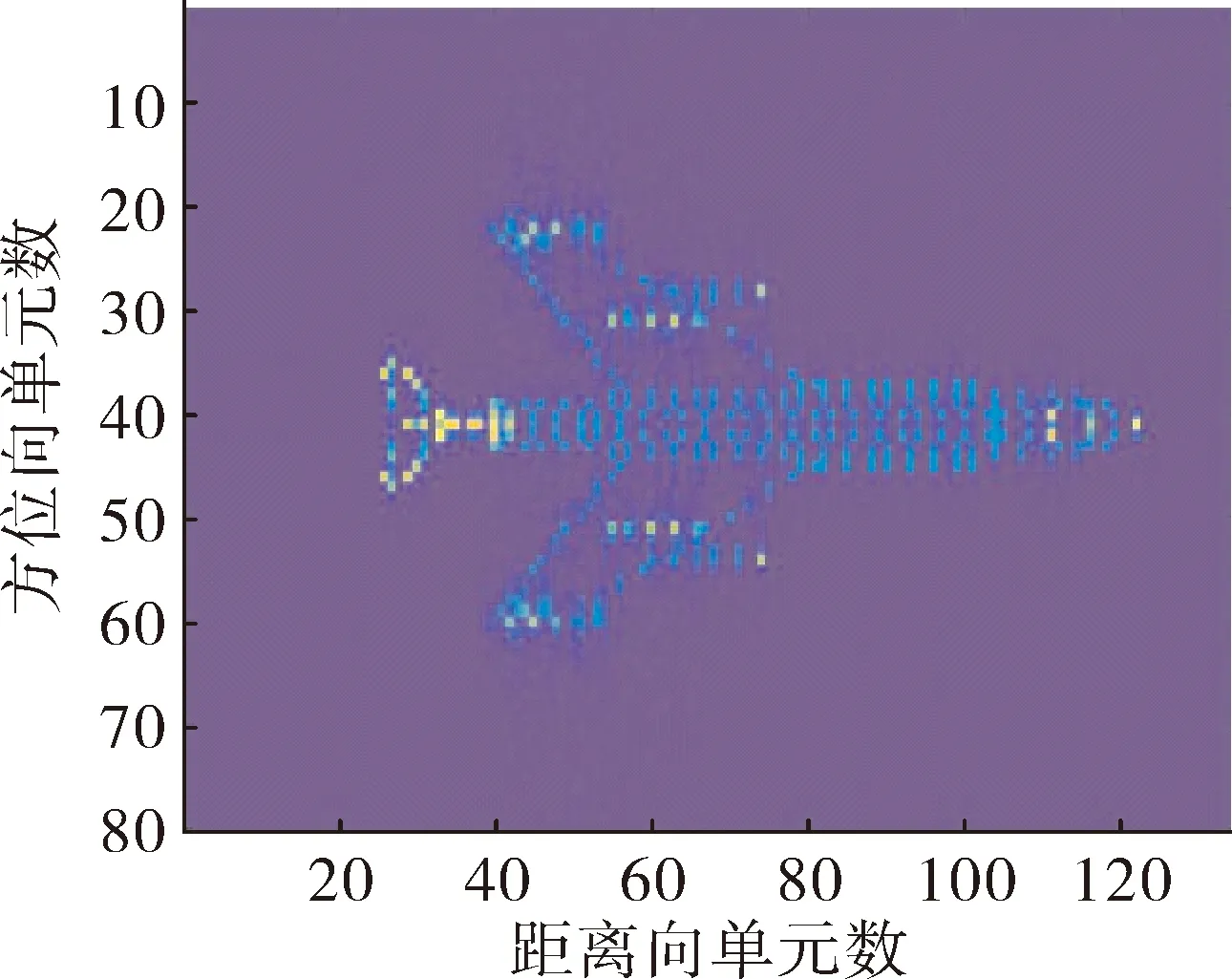
图8 正负线性调频信号CS波形分离并成像

对以上3种波形成像效果的图像熵(image entropy,IE)[9]进行量化比较。

(17)

其中,I代表目标图像,Sum{·}为对图像所有元素值的求和操作。该指标可以反映图像中目标的聚焦性能,聚焦效果更好的目标图像将具有更低的aIE值。表1给出了各成像结果的定量评价,可以看到使用正负线性调频信号的指标最好,OFDM-chirp略次之,而相位编码的次之,且压缩感知波形分离方法比匹配滤波效果好。

表1 不同波形成像结果的评价指标值

4 结论

基于压缩感知的波形分离方法突破了匹配滤波的理论限制,为MIMO雷达波形分离提供了全新的方法,该方法不仅能够具有很好的旁瓣抑制效果,能够有效抑制非正交波形的互耦噪声而且CS波形分离方法的距离分辨率取决于采样频率而非信号带宽,由于采样频率通常大于信号带宽,因此利用CS波形分离方法可以一定程度上提高距离向分辨率。该方法发射波形集影响感知矩阵的构造从而影响波形分离效果,文中分析出感知矩阵列相关系数与发射波形相关性的关系,分析了3种波形的相关性能,仿真得出了正负线性调频信号应用于压缩感知波形分离,效果最优。