浅析借助几何直观解决数学中的类“线段条数”问题

张芳芳

摘 要：几何直观就是依托几何图形和直观物体进行数学的思考、想象。几何直观是义务教育阶段新课程标准中提出的10个核心概念之一，需要我们在数学教学中借助相关内容有机的去发展学生的几何直观素养。本文借助同一平面中的几个点可以组成几条不同的线段模型，来解决同类问题，以下称为类“线段条数”问题。

关键词：几何直观 线段条数问题

一、几何直观的意义

义务教育数学课程标准指出：“几何直观主要是指利用图形描述和分析问题。借助几何直观可以把生活中复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测或获取结果。”[1]在研究数学问题的过程中，几何直观可以将生活中具体形象问题转化为抽象数学几何图形问题，使问题变得简明、清晰。学生借助几何直观进行思考、猜想、验证，进而获得结论或者推翻假设，达到问题解决和能力的提升。几何直观能力的培养至关重要，它是我们逻辑思维形成和发展的起点。

二、线段条数问题

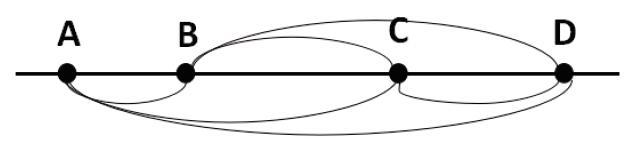
线段条数问题：是指平面中或者一条直线上有几个不同的点，可以组成不同的几条线段。如图，直线上有四个不同的点，可以组成几条不同的线段？你有什么发现？（图1）

学生借助以下几何直观方法：线段图、树状图、列举法、归纳公式法。（这四种方法在以下具体问题中体现）

三、类“线段条数”问题的解决

以下问题都可以抽象为类“线段条数”问题加以解决：

（1）在中外领导人的会晤中，按礼节要握手。若每两人握1次手，则3个人共握几次手？4个人共握几次手？

（2）象棋比赛中，所有比赛选手要进行两两对弈，若有3人，则一共下几局，若有4人呢？5个人呢？……n个人呢？

（3）一列高铁往返于两城市之间，每次运行停靠n个站点（包括起点站和终点站）。请问铁路部门共应发售多少种不同的车票？

问题（1）是简单的组合问题。主要安排在义务教育数学课程标准要求的第二学段，青岛版教材四年级上册和五年级下册进行学习，重点在于培养学生借助几何直观，为解决问题提供思路。问题（2）是在问题（1）基础上对研究对象的扩展到无数（进一步渗透极限思想），引导学生借助几何直观找到解决方法。并帮助学生理解、记忆和应用数学学习中发现的规律或总结的结论，为初中和高中学习排列与组合打下良好的基础。

问题（1）、（2）是典型的类“线段条数”问题。此阶段学生抽象思维开始发展，借助几何图形引导学生思考拓展学生的想象力。将研究对象“人”抽象为一个点，把“两人握手或比赛”抽象成“两点之间连接成的线段”，借助直观图形就可以简明地解决问题。

其解决方法是：

方法一：线段图（如图2）。借助几何直观直接在图上数出线段条数，数的时候要避免重复和遗漏。提醒学生从“A”开始依次与其后边“B、C、D”全部完成握手，接着从B开始依次与其后边的人握手，直至结束。当“B”与其余人握手时，注意不能与“A”重复握手，最后数出所有次数：共计6次。

方法二：树状图（如图2）。用简单的树状图直观展示出组合结果。

得到结果：四个人两两握手共握6次。

方法三：列举法。列举法是将所有符合题意的结果一一列举出来。是学生思维发展到更高阶段出现的，此时学生的空间想象能力得到进一步发展，逻辑思维、空间观念和推理能力得到一定发展，有的学生无需借助几何图形，将研究对象抽象为字母或者符号，逐一列举出对应组合，直观的数出结果，从而解决问题。此法用于研究对象有限且数据较小时。

如四人两两握手列举如下：AB AC AD

BC BD

CD 得到结果：共计6次。

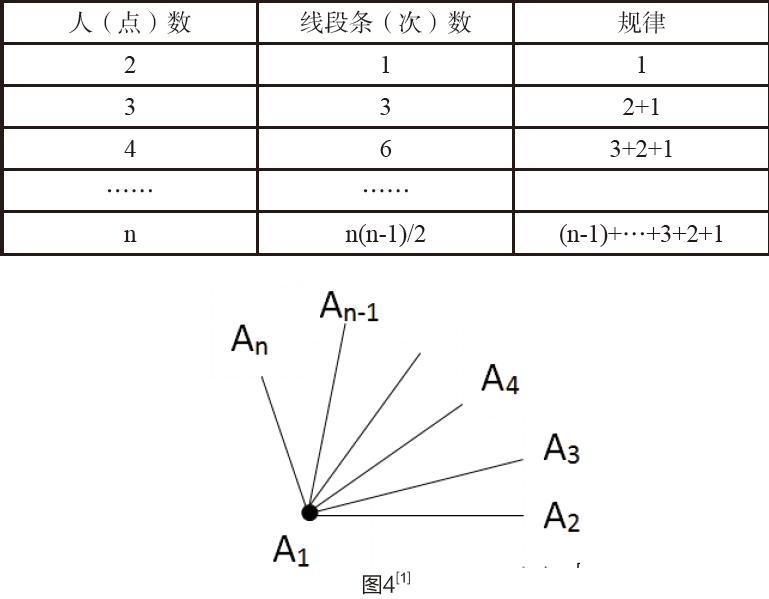
方法四：归纳公式法。当第二个问题扩展为n个人时，可采用几何图形或图表的力量进行归纳，总结出规律或归纳出公式直接应用。人（点）数 线段条（次）数 规律

2 1 1

3 3 2+1

4 6 3+2+1

…… ……

n n（n-1）/2 （n-1）+…+3+2+1

综上可知，生活中的握手问题，双人对弈或者选手两两比赛问题，实际上都是简单的组合现象，皆可抽象为“线段条数”问题 ，借助以上四种几何直观的方法，可以直观的简明的解决。此式（n-1）+…+3+2+1的求解方法，即对于n个点中的任何一个点都可以与其余的（n-1）个点组成（n-1）条线段，但每一个组合都重复算了一次，故共計线段条数n（n-1）/2条。或者向学生讲解采用高斯求和公式进行计算。

问题三“车票问题”和“握手问题”有所不同，其中蕴含着排列思想。学习时若将“车票问题”看成“线段问题”，这里的线段有方向的，是矢量，从A至B是一种车票，从B至A是另一种不同的车票，学生借助先前经验，得出结论就是“线段问题”的二倍，即n（n-1）。将组合和排列理解透彻。

结语

随着知识难度的扩展和深化，早期几何直观模型的建立至关重要，我们生活的是一个多维空间，要进行归纳探究规律解决生活中一些常见的问题，势必要采用数形结合即几何直观的方法，它是学生发展空间观念的重要媒介，是数学研究和发展的一种重要方法。在日常教学中，我们要重视培养学生的这种能力。

参考文献

[1]义务教育数学课程标准（2011版）解读[M].北京师范大学出版社，2012.200.