基于声场模信号特征和多项式拟合的声速剖面反演技术研究
2019-12-23刘福臣姬托张巧力
刘福臣, 姬托, 张巧力
(1.声纳技术重点实验室, 浙江 杭州 310023; 2.杭州应用声学研究所, 浙江 杭州 310023)
0 引言
自1976年Bucker[1]提出匹配场处理(MFP)方法以来,与匹配场和声学建模有关研究在过去的几十年里得到了迅速发展。在海洋声场数值计算[2-3]基础上,MFP可以通过模型与数据的匹配来反演环境参数或估计目标距离,并选择合适的算法。另外,失配是制约匹配场性能的主要问题,包括环境失配和系统失配,环境失配包括声速剖面、海底特性不确定,系统失配包括阵列倾斜、水听器相移等。
在海洋环境获取技术中,声速剖面主要利用多个测量声速矩阵的正交分解,得到特征值所对应的特征向量,再将其表示为经验正交函数(EOF)的形式获得。沈远海等[4]已经验证了在浅海环境下利用EOF表示声速剖面的可行性。张镇迈等[5]也尝试了在深海中声速剖面的EOF表示并实现了声速梯度的反演。Li等[6]利用基于水平线阵的匹配场反演方法来反演声速剖面并通过南海海域数据进行了验证。何利等[7]和Yu等[8]详细研究了匹配场反演声速剖面的可行性。何利等其他学者[9-20]对不同海域的声速剖面反演展开研究。然而在不熟悉声速剖面情况下,反演声速剖面则较为困难,同时由于温盐深仪(CTD)/抛弃式温深仪(XBT)等声速剖面测量仪器的相关费用,水声学面临的一个挑战是如何开发单传感器的声速剖面反演方法。
由于垂直阵反演面临阵形失配的问题,在实际应用中难以准确实现参数反演,因为阵形带来的失配远比声速参数失配要严重,同时在实际声纳设备中,没有垂直孔径的基阵可供参数反演,因此本文瞄准单水听器开展参数反演的研究。
本文提出了一种基于模信号[5]和多项式拟合的声速剖面反演方法,该方法采用多项式拟合声速剖面,与EOF法不同,该算法具有低阶多项式拟合的特点,通过理论推导和仿真分析,证明了该方法基于单水听器接收的模信号进行声速剖面反演的可行性,并通过海上试验数据验证了该方法的可行性。
1 基础理论
1.1 模信号及其特性
依据简正波理论,单水听器的接收声压可简写为
(1)
(2)
(3)
式中:r为接收水听器与目标间水平距离;z为接收深度;zs为目标深度;krm为第m号模态的本征值,ψm(z)为第m号简正波的本征函数;ρ为海水密度;H为海洋深度;M为模态数目;f为频率;S(f)为声源频谱。
定义第m号模信号Hm(r,z,f)频域表达式为
(4)
相应的时域表达式为
(5)
在时域中,接收信号源自源信号s(t)与一系列模信号的卷积:
(6)
图1(a)为Munk剖面,图1(b)为深海传输函数,该函数可清楚地分为两部分:第1部分(t=39.8 s)是海洋折射模信号簇;第2部分(t=41.5 s)是来自海底和表面反射的模信号簇。
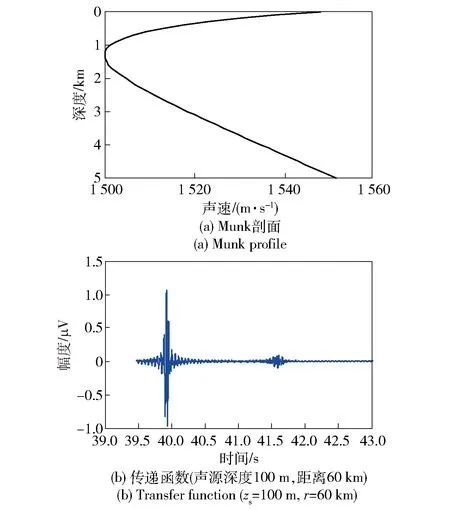
图1 深海声速剖面和模信号Fig.1 Deep sea sound velocity profile and mode signal
1.2 基于多项式拟合的声速剖面表示方法
采用n阶多项式拟合声速剖面c(z)表示为
(7)
式中:
(8)
c(n)(0)为c(z)的n阶导数。
典型深海声速剖面如Munk,其具有完整的公式化表示:
(9)
式中:
(10)
利用多项式进行Munk声速剖面的拟合,验证声速剖面近似表达的可行性,则声速可以表示为
(11)
式中:b1=1 466.835;b2=0.017;b3=11.055;k0=2;k1=-0.001 5.
进行n+1阶Taylor展开,表示为
c(z)≈b1+b3ek0+(b2+b3k1ek0)z+
(12)
多项式拟合系数分别为
(13)
图2给出了不同拟合阶数n的声速剖面。由图2可以得出结论:1)对于典型Munk声速剖面,拟合阶数越高,全海深声速剖面的贴合程度越高;2)不同拟合阶数对浅表层的声速剖面的贴合程度都非常高,虽然低阶展开无法实现全海深的声速剖面准确拟合,但5阶情况下对声道轴以浅的水文拟合比较好。当允许一定的误差存在时,采用较低的阶数是可以进行声速剖面拟合的。
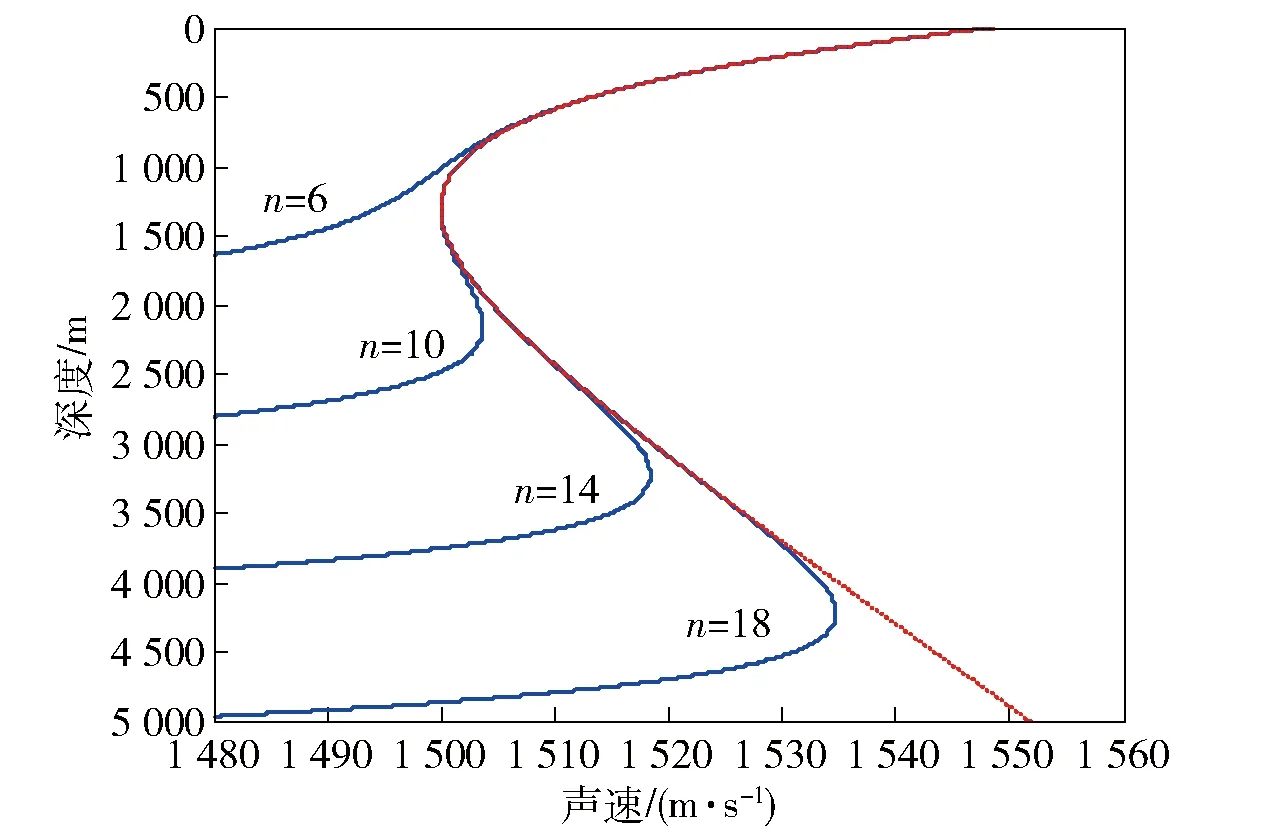
图2 不同拟合阶数下声速剖面对比曲线Fig.2 Contrast diagram of fitting sound speed profile using different coefficients
图3(a)给出了2 000 m海深的情况,分别采用3阶、4阶和5阶多项式拟合,其中:3阶拟合声速剖面平均误差为0.58 m/s、均方根误差为0.68 m/s;4阶拟合声速剖面平均误差为0.11 m/s、均方根误差为0.13 m/s;5阶拟合声速剖面平均误差为0.02 m/s、均方根误差为0.02 m/s.

图3 不同拟合阶数下声速剖面对比曲线Fig.3 Contrast diagram of fitting sound speed profile using different orders
图3(c)给出了4 000 m海深的情况,分别采用3阶、4阶和5阶多项式拟合,其中:3阶拟合声速剖面平均误差为2.1 m/s、均方根误差为2.6 m/s;4阶拟合声速剖面平均误差为0.77 m/s、均方根误差为0.93 m/s;5阶拟合声速剖面平均误差为0.23 m/s、均方根误差为0.29 m/s.
通过以上理论和仿真分析,对于实际声速剖面,在反演误差一定情况下,可以采用低阶多项式拟合表层声速剖面,在下面行文中,分析两种声速剖面,其中:2 000 m海深声速剖面采用4阶多项式拟合,平均误差可控制在0.12 m/s以内;4 000 m海深声速剖面采用5阶多项式拟合,平均误差可控制在0.3 m/s以内。这对于声场预报和实际应用基本可以满足需要。
为验证多项式拟合性能,选取南海与西太平洋典型海区声速剖面进行分析。查海洋环境数据库,海区1为台湾以东海域(东经125.8° 北纬23.3°)、海区2为台湾以东海域(东经123°,北纬23°)、海区3为南海北部(东经16° 北纬20°)声速剖面分别如图4~图7所示(测量声速剖面为历年平均值)。图4(a)、图5(a)、图6(a)和图7(a)分别给出了测量声速剖面与反演声速剖面的对比结果,图4(b)、图5(b)、图6(b)和图7(b)分别给出了测量声速剖面与反演声速剖面的反演误差,声速剖面反演平均误差分别为0.4 m/s、0.38 m/s、0.3 m/s和0.4 m/s,证明利用多项式进行深远海声速剖面表征是可行的。由数据库查询的声速剖面为历史平均值,由于测量数据本身存在误差,尤其是0~500 m深度区间。
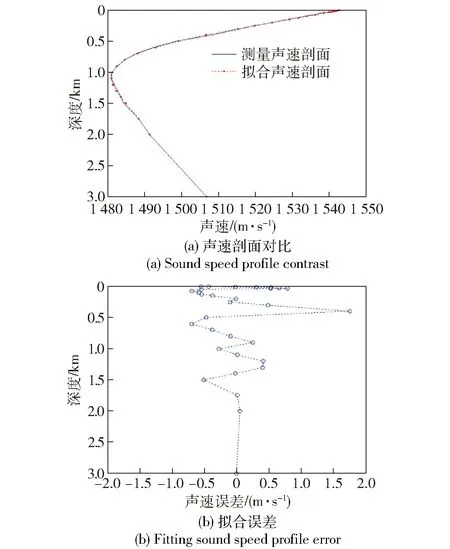
图4 海区1(6月份)测量声速剖面与拟合声速剖面对比Fig.4 Comparison of sound speed profile measured in sea area 1 (June) with fit sound speed profile

图5 海区2(6月份)测量声速剖面与拟合声速剖面对比Fig.5 Comparison of sound speed profile measured in sea area 2 (June) with fit sound speed profile
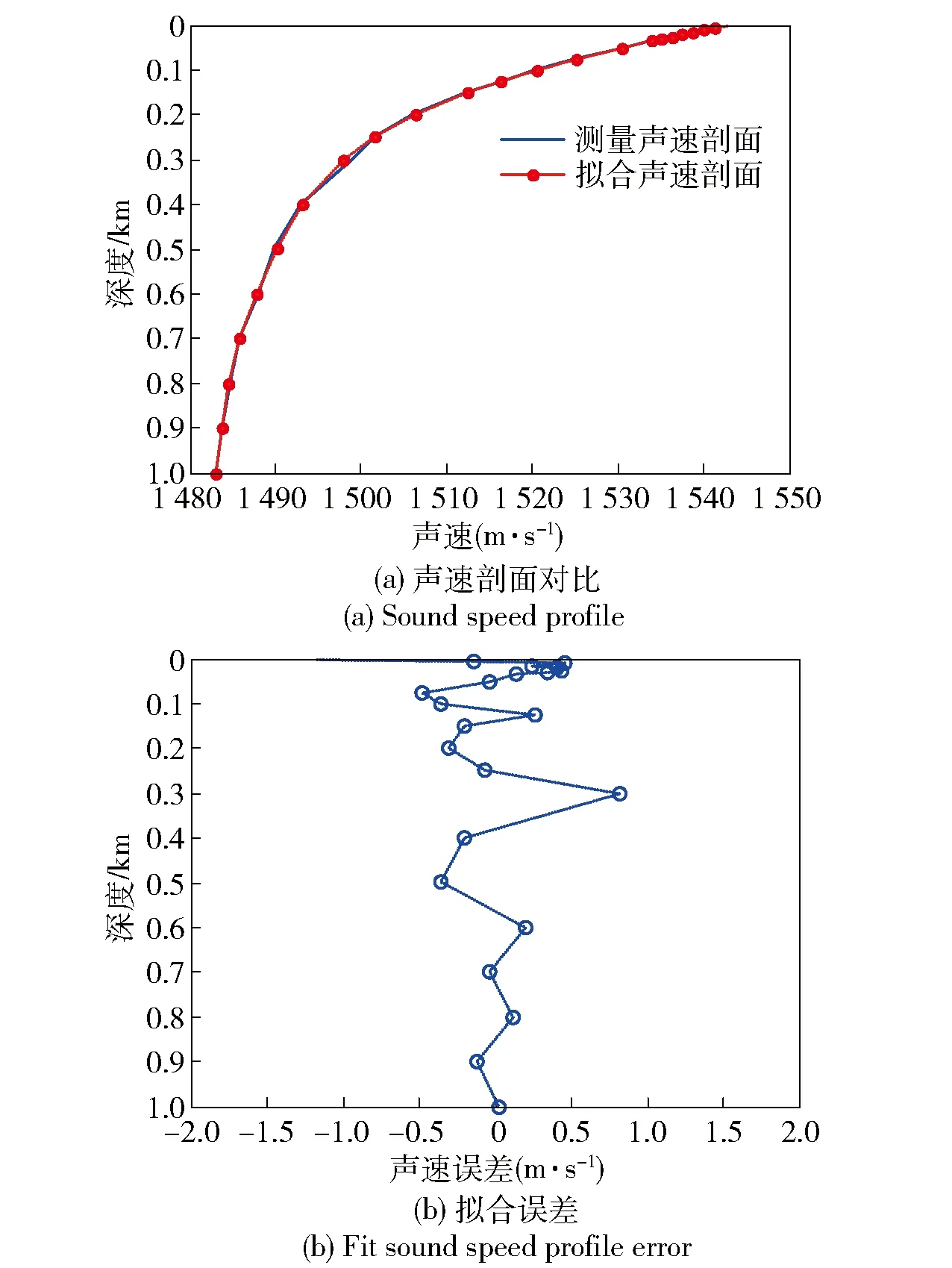
图6 海区3(6月份)测量声速剖面与拟合声速剖面对比Fig.6 Comparison of sound speed profile measured in sea area 3 (June) with fit sound speed profile
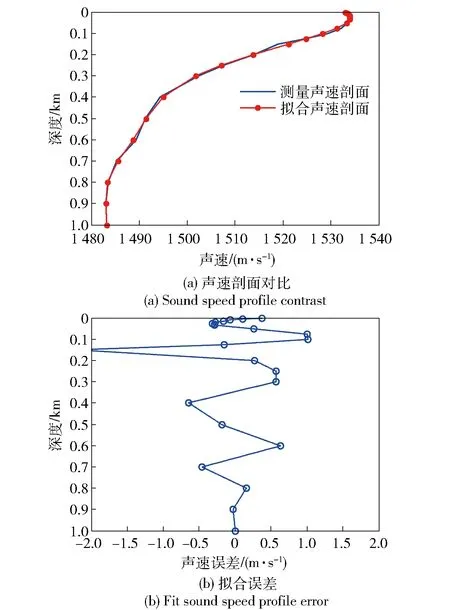
图7 海区3(12月份)测量声速剖面与拟合声速剖面对比Fig.7 Comparison of sound speed profile measured in sea area 3 (December) with fit sound speed profile
鉴于深海声速剖面在较大深度处基本稳定,同时也为了减小测量误差和反演时间,因此本文在深度大于2 000 m时采用历史平均值处理,主要反演深度2 000 m以下的部分。
2 反演算法
深海中的垂直列阵(VLA)如图8所示,海底由基底层组成,其中cb、ρb、αb分别表示基底层的声速、密度和吸收系数。因此,当确定海底参数时,所需的反演参数包括系数向量。

图8 接收垂直线阵与反演参数Fig.8 Received VLA and Inversion parameters
接收垂直阵的第k个单元在时域和频域可以表示为p(r,zk,t)与P(r,zk,f),垂直数据向量B可以用(14)式表示:
(14)
在反演算法中,拷贝信号Pe(r,zk,f)是通过简正波模型得到的。在这里,拷贝垂直向量P可以表示为
(15)
Bartlett匹配处理器如(16)式所示:
(16)
式中:fl为下限频段;fh为上限频段。
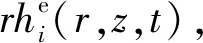
拷贝模信号与测量模信号匹配同样采用Bartlett匹配处理器处理,如(17)式所示:
(17)
遗传算法(GA)采用数学仿真软件MATLAB GA工具箱中基于全局搜索参数空间的交叉启发式函数,该处理器具有多径压缩能力,适用于高信噪比条件。
3 仿真分析
以Munk声速剖面为参考,开展不同条件下的声速剖面反演,仿真分析的思路:1)首先进行垂直阵条件下声速剖面反演可行性分析;2)接着进行基于单水听器接收的模信号声速剖面反演;3)再论证在非海面海底传播模式的声速剖面反演可行性。在下面仿真中,多项式拟合系数均采用5阶来处理,反演参数是采用参数空间遍历进行的,同时结合参数的合理性。在选取参数时,依据声速剖面的合理性进行选择,如最后一项对应声速的常数项部分,选择从1 460~1 560 m/s的区间内选择。
在实际反演处理中,对深海声速剖面在大深度上相对稳定,因此在处理时采取2 000 m以浅采用多项式拟合(为获取声道轴深度,扩大了拟合的深度范围),2 000 m以深进行采用历时平均值处理。
3.1 利用垂直阵的声速剖面反演
表1给出了利用垂直阵的声速剖面反演仿真参数,其中:海区深度为4 000 m,声速剖面为典型Munk剖面,声道轴深度为1 300 m;目标距离为30 km,深度100 m,接收基阵均匀布放在100~200 m之间,阵元间距为7.5 m;处理频段采用20~40 Hz.
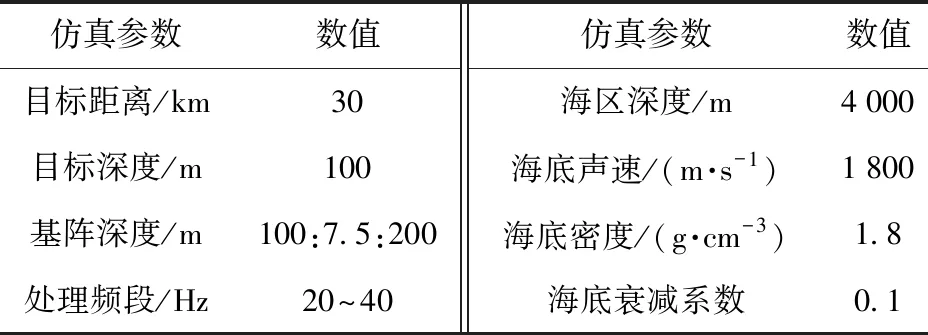
表1 利用垂直阵的声速剖面反演仿真参数
本例调用KRAKEN模型的次数为20 800次,GA在代价函数值小于6.93×10-8时停止搜索,计算时间为120 min. 表2给出了搜索结果。图9和图10给出了声速剖面反演结果,拟合声速剖面与仿真剖面吻合,声道轴深度相同,在全海深声速剖面平均反演误差为0.14 m/s.
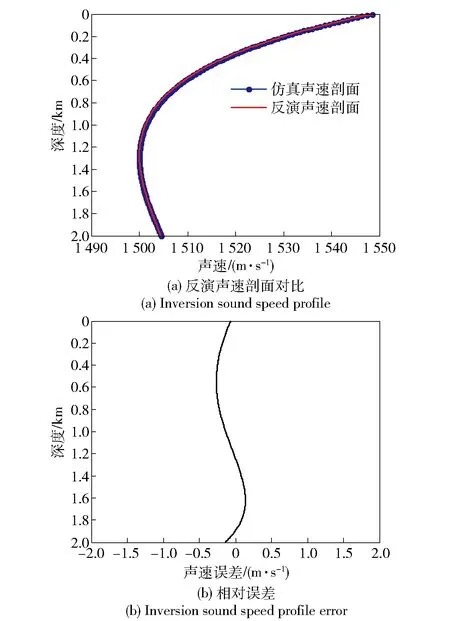
图9 仿真剖面与反演声速剖面比较Fig.9 Comparison of real sound speed profile and inversion sound speed profile
但在实际海洋波导中,基于垂直阵的参数反演存在缺陷在于,大深度垂直阵阵形难以测量,这会给参数反演带来较大误差;实际应用中,声纳平台没有较大垂直孔径,难以满足垂直阵反演的要求。因此,基于单平台、单节点的声速剖面反演更具实际意义和工程应用前景。

表2 多项式拟合参数反演结果
3.2 利用单水听器模信号的声速剖面反演
研究结果表明:垂直阵阵形失配对反演影响远比环境参数失配要严重,因此本文瞄准单水听器开展参数反演的研究。下面给出利用单水听器接收的模信号进行声速剖面反演的仿真结果。
表3给出了利用单水听器模信号的声速剖面反演仿真参数,其中:海区深度为2 000 m,目标距离为60 km,深度100 m,水听器接收深度在100 m之间;处理频段采用20~40 Hz.

表3 利用模信号的声速剖面反演仿真参数
本例调用KRAKEN模型的次数为20 800次,GA在代价函数值小于5.479×10-8时停止搜索,计算时间为120 min. 表4给出了搜索结果。图11和图12给出了声剖面反演结果,拟合声速剖面与仿真剖面吻合,声道轴深度相同,全海深声速剖面平均反演误差在0.15 m/s以下,算法性能与垂直阵反演接近,证明基于单水听器模信号反演是可行的。

表4 多项式拟合参数反演结果
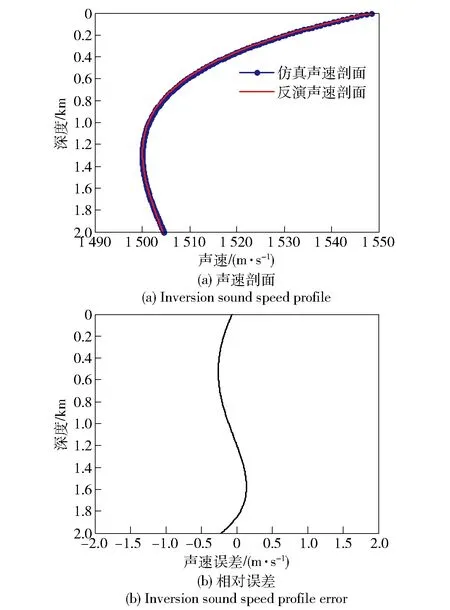
图11 仿真剖面与反演声速剖面比较Fig.11 Comparison of real and inversion sound speed profiles
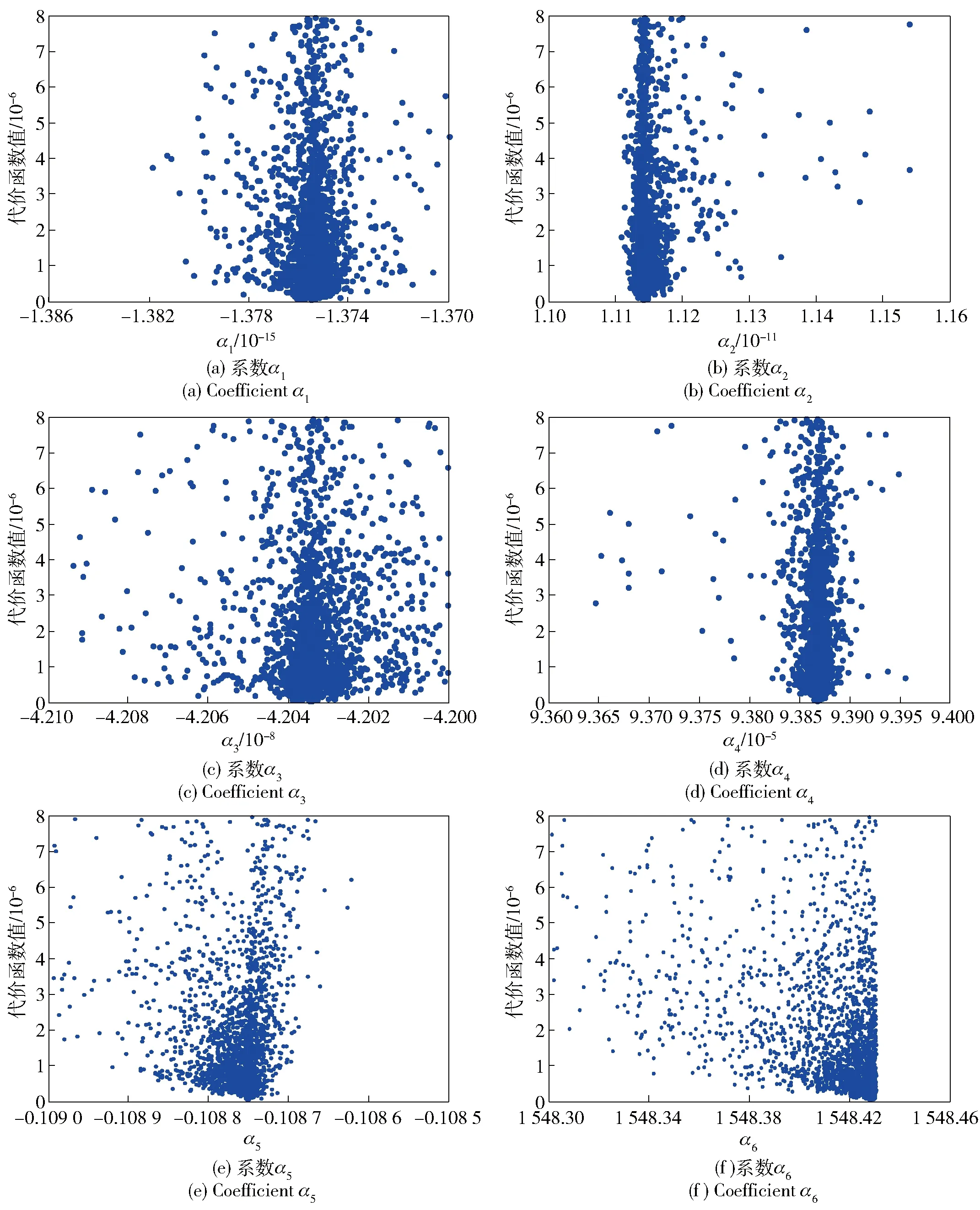
图12 利用模信号的声速剖面反演参数收敛图Fig.12 Inversion parameters
3.3 利用单水听器非海面海底反射模信号的声速剖面反演
当海底参数未知,基于单水听器反演不会得到好的结果,因为存在海底海面反射模式,是受海底参数(包括海底起伏、海底分层结构及其各层声学参数)影响的。只有利用非海面海底反射(SRBR)模信号才能减小环境参数失配带来的影响。
表5给出了利用垂直阵的声速剖面反演仿真参数,其中:海区深度为4 000 m,目标距离为30 km,深度100 m,水听器接收深度在100 m;处理频段采用20~40 Hz. 这里采用非SRBR模信号进行反演,如图11所示。

表5 利用非SRBR模信号的声速剖面反演仿真参数
结果如表6所示,本例调用KRAKEN模型的次数为20 000次, GA在代价函数值小于6.997×10-8时停止搜索,计算时间为120 min. 图13和图14给出了声速剖面反演结果,拟合声速剖面与仿真剖面吻合,平均误差0.16 m/s,基本可以满足环境参数测量的需求。图15为基于简正波模型计算得到的非SRBR信号。这一仿真结果表明,利用非SRBR模信号反演可以减小海底参数失配的影响,提升在海底参数未知条件下的反演性能。
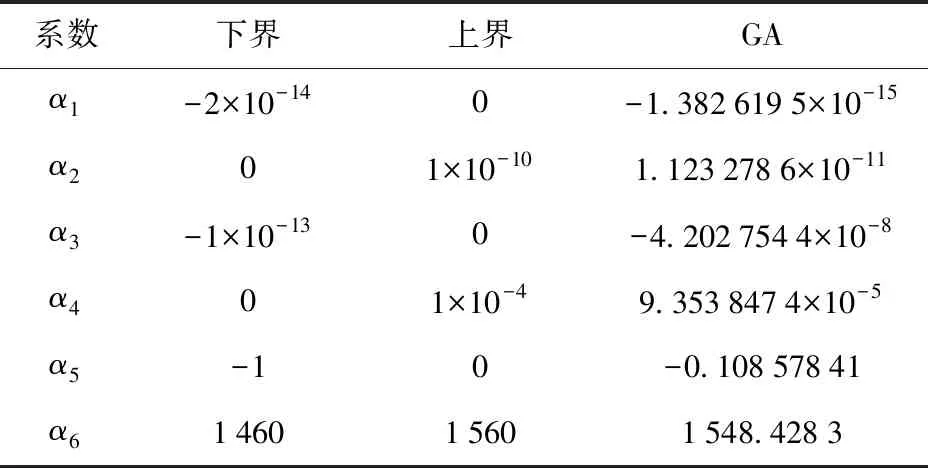
表6 多项式拟合参数反演结果
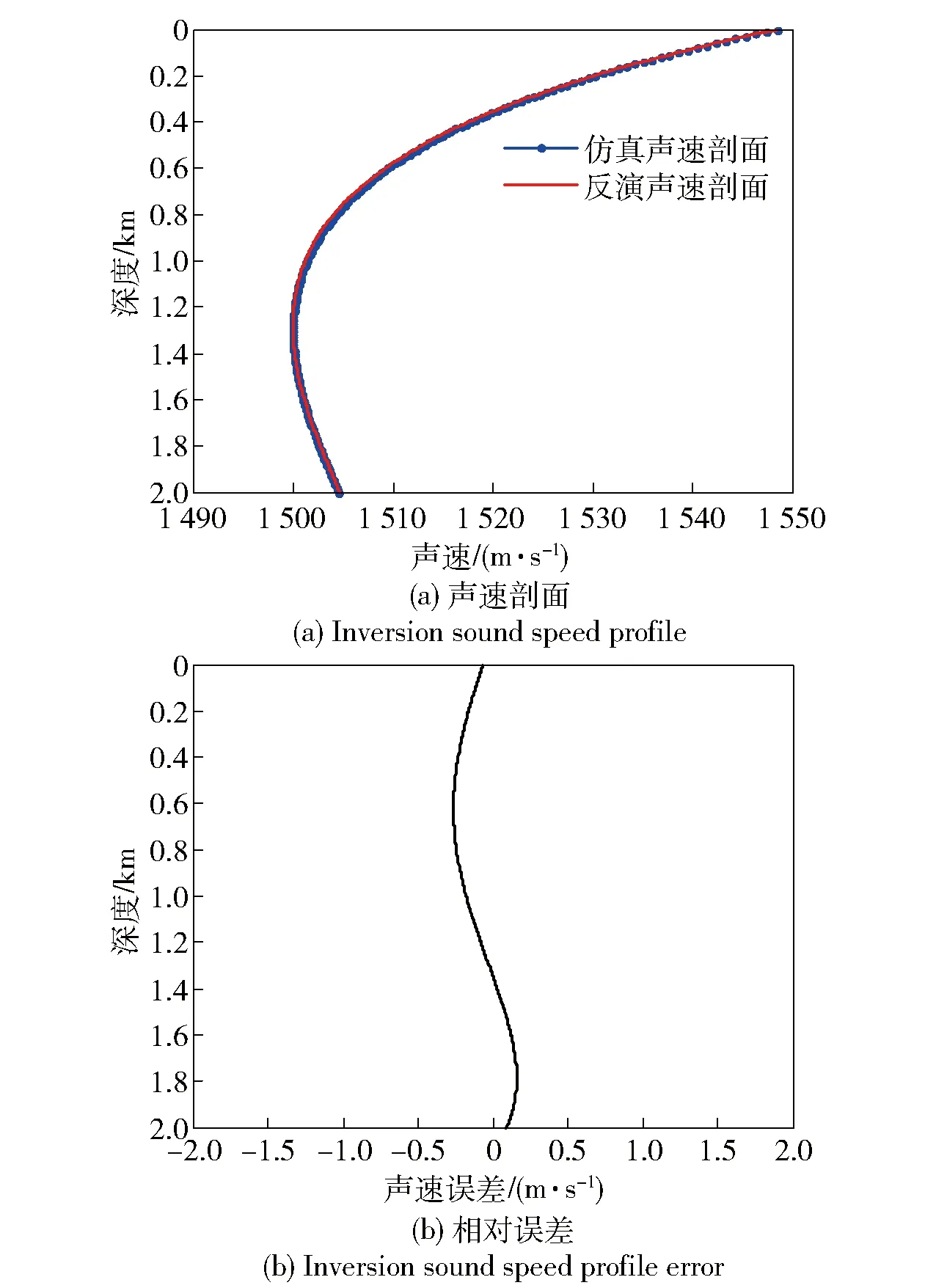
图13 仿真剖面与反演声速剖面比较Fig.13 Comparison of real and inversion sound speed profiles

图14 利用非SRBR模信号的声速剖面反演收敛图Fig.14 Convergent graphs of sound speed profile inversion parameters based on non-SRBR mode signal

图15 非SRBR模信号Fig.15 Non-SRBR mode signal
前面对垂直阵、单水器和非SRBR单水听器3种情况下反演参数进行对比分析,在相同环境条件下(海深均为4 000 m,声道轴深度为1 300 m,目标距离为30 km、深度为100 m,处理频段均为20~40 Hz),在海底参数、阵形或阵元未知(不失配时)、3种方法基本相当,获得声速剖面与实际吻合,证明本文提出方法是可行的。而且该算法优势在于:1)当阵形失配时,利用垂直阵反演将无法获得好的结果;2)当海底参数未知,基于单水听器反演将不会得到好的结果,因为存在海底海面反射模式,是受海底参数影响的;3)当海底参数未知,利用非SRBR信号的声速剖面反演仿真仍然能得到好的结果。下面利用海试数据进行验证。
4 海试数据处理
2018年5月进行了深海基础性试验,试验区域海深约为3 750 m,声速剖面如图16所示。表面声速接近1 542 m/s,海底声速约为1 520.7 m/s,试验测线海深最大起伏约为950 m.
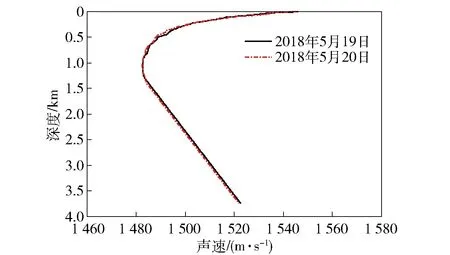
图16 测量声速剖面Fig.16 Sound speed profiles on sea areas
图17为试验海域的水深分布,自容式潜标布放在图17原点位置处,海深约为2 800 m,最远投弹点海深为3 750 m.

图17 深水声传播测线海深分布Fig.17 Water depth of sea test route
对接收深度为30 m和40 m的水听器接收信号进行分析,验证该方法的反演性能,爆炸声源距离为48.9 km、深度为200 m,如图18和图19所示。
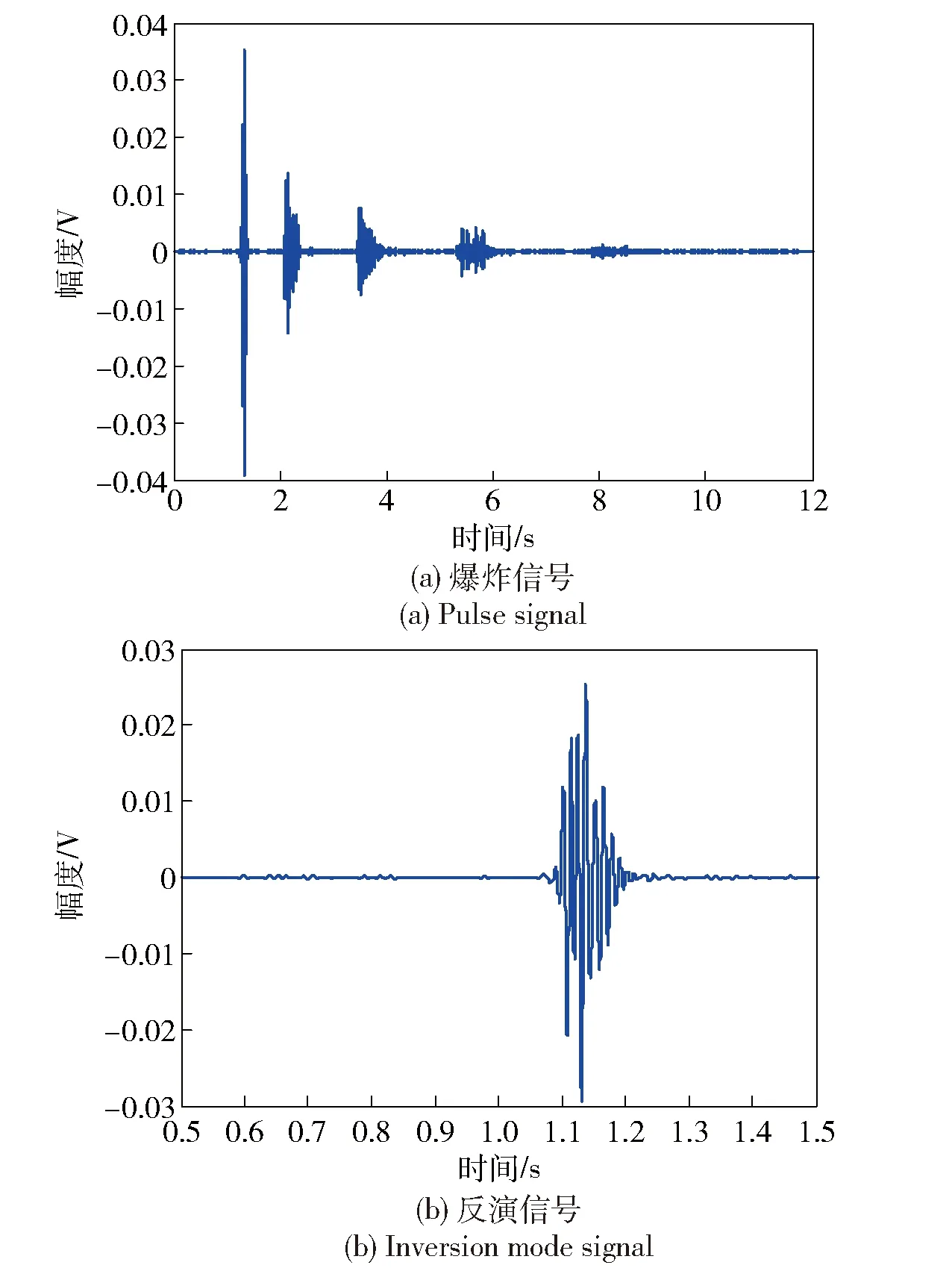
图18 接收信号(距离48.9 km、深度300 m)Fig.18 Signal received by the hydrophone (distance: 48.9 km, and depth: 300 m)
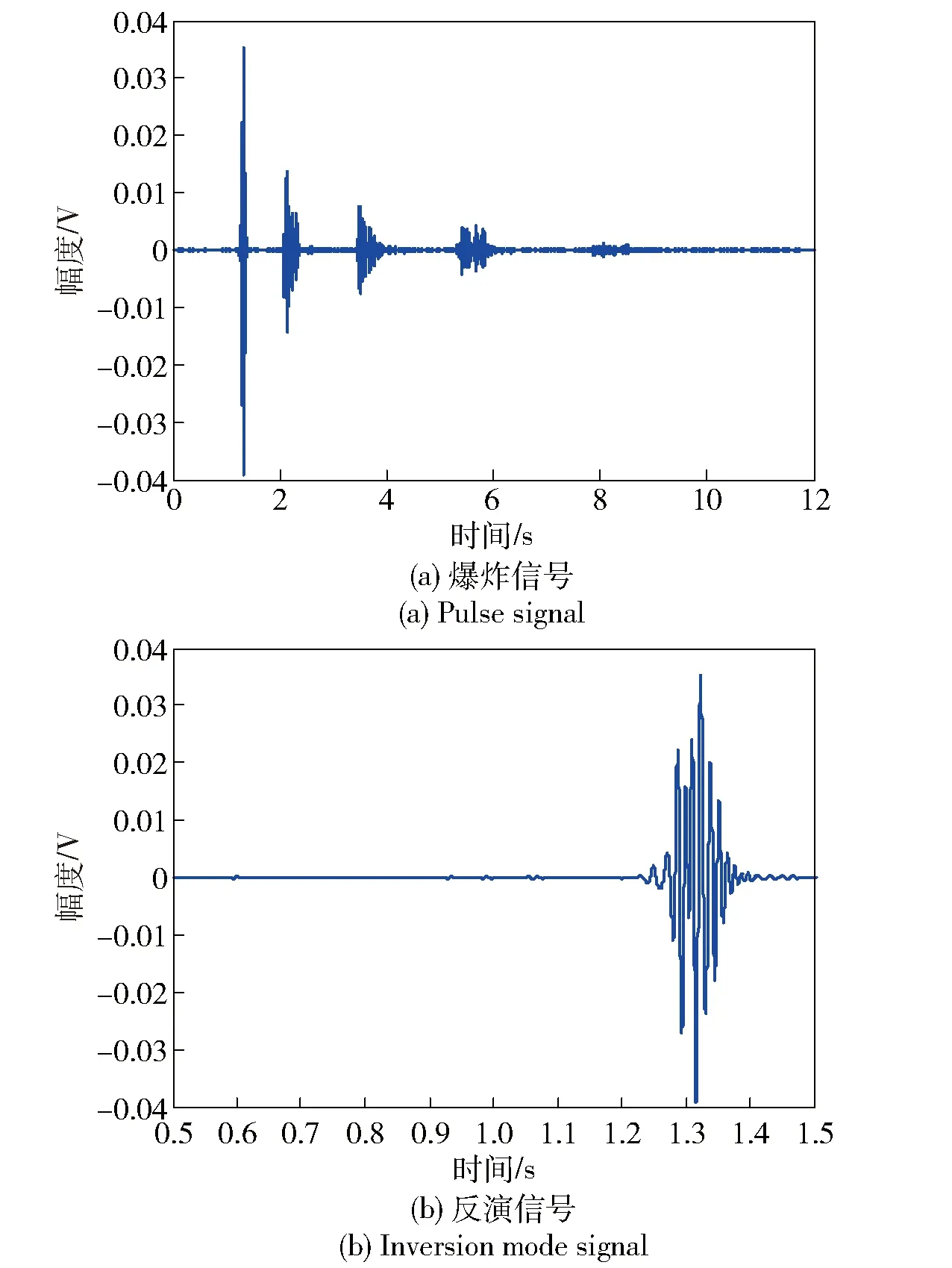
图19 接收信号(距离48.9 km、深度400 m)Fig.19 Signal received by the hydrophone (distance: 48.9 km, and depth: 400 m)
图18(a)是水听器接收深度为300 m的脉冲信号,图18(b)是选择的反演信号,它主要由非SRBR模式信号组成。图19(a)是水听器接收深度为400 m的脉冲信号,图19(b)是选择的反演信号,它同样由非SRBR模式信号组成。
表7列出了每个参数的收敛值。图20给出了声速剖面反演的结果。由表7可以看出,反演的声速剖面与实测的声速剖面是一致的,声道轴的深度是一致的。

表7 多项式拟合参数反演结果

图20 测量声速剖面和反演声速剖面对比Fig.20 Comparison of measured and inversion sound speed profiles
图21为不同深度的声速剖面误差。该数据反演结果表明:反演声速剖面在100 m以浅误差较大,在0~100 m深度范围内反演误差接近1.14 m/s;在100~2 000 m深度反演误差误差小于0.2 m/s. 由于非SRBR模式信号对海底参数不敏感,这种方法可以解决海底参数未知情况下的声速剖面反演问题。
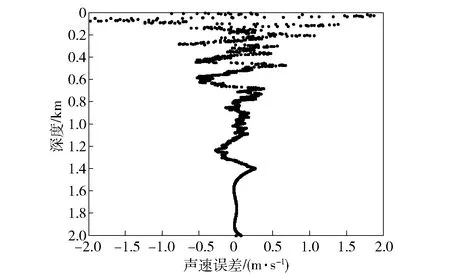
图21 测量声速剖面和反演声速剖面误差Fig.21 Inversion sound speed profile error
5 结论
本文介绍了模信号的概念和深海分布特性,通过理论分析和仿真分析,证明低阶多项式拟合可用于深海声速剖面的表征;在此基础上,提出了利用基于声场模信号特征和多项式拟合的声速剖面反演技术研究,并对比分析了基于垂直阵、单水听器、非SRBR信号的反演性能;最后利用海试数据验证了反演算法的可行性。主要结论如下:
1) 采用5阶多项式拟合可以实现对2 000 m以浅的声速剖面较精确的表征。
2) 提出的反演算法适用于垂直阵、单水听器。海底参数与阵形已知条件下反演性能基本相当,但单水听器数据的反演更具应用前景。
3) 当海底参数未知条件下,采用单水听器接收的非SRBR模信号可以实现对共轭深度以下声速剖面的准确反演,适用陌生海域的海洋环境信息获取。
