小型油动无人直升机机架振动特性与试验研究

2019-12-22娄尚易薛新宇崔龙飞肖会涛田志伟

农机化研究 2019年5期

娄尚易，薛新宇，顾伟，崔龙飞，肖会涛，田志伟

(农业部南京农业机械化研究所，南京 210014)

0 引言

农用植保无人机利用无人机搭载喷药装置，通过地面遥控或航空飞控实现喷洒作业。农用飞机空中作业效率高，突击能力强，利于消灭暴发性病虫害[1]。其适合在房居与耕地交混的农作区及丘陵山地等复杂地理条件的耕地进行施药作业，在地面机具无法进入的水稻和高秆作物病虫害防治作业中具有无可替代的作用。目前，国内无人机企业已近400家，从事农用植保无人机研发与生产的企业也越来越多并呈快速增长趋势。

按照农用植保无人机动力来源划分，目前主要分为油动农用植保无人机与电动农用植保无人机两类。与电动无人机相比，油动无人机具有较好的抗风能力，续航时间长，续航能力强；缺点是由于现有民用无人机大多数采用航模发动机，发动机稳定性差，工况复杂，致使油动无人机的振动大，不易掌握，对油动无人机在作业过程中的安全性、施药规范、操作水平要求更高。油动无人直升机在航空作业过程中由于受到发动机、旋翼、传动箱的动力载荷激励与无人机表面附面层紊流强度的影响，导致机身及相连施药关键部件的振动，若机体与喷杆连接点的激励频率与喷杆的固有频率接近或相等，则会引起两者的共振，强烈的振动甚至会影响无人直升机的飞行姿态。目前，有关植保无人机在施药过程中的相关研究大多集中在喷雾参数[2-5]、施药技术[6-10]、航空喷嘴研究[11-14]等方面，很少关注机架结构的振动特性及喷杆在激励频率下的频响特性，但在其他用途直升机及地面施药机具中涉及相关研究[15-19]。本文以避免喷杆与机体发生共振、保证无人机的安全飞行为研究目的，以某型油动植保无人直升机机架为研究对象，利用PROE三维软件对无人机机架进行建模，最终完成有限元模型的建立；同时，应用ANSYS有限元分析软件对机架有限元模型进行模态分析，使用SO模态试验与分析软件通过模态试验验证有限元模型的准确性，即采用模态仿真分析结合试验验证的方法获得无人机机架的振动特性，为后续的研究提供理论依据。

1 油动植保无人直升机机架结构

某型油动植保无人直升机机架由机身框架、起落架、尾管、斜支撑、喷杆及其他支撑连接部件组成，如图1所示。机身框架是安装发动机、传动箱、旋翼、药箱、油泵、飞控箱及水泵等结构的装置，决定了整机组成的结构布局，是无人直升机的核心部件。起落架是唯一支撑整架无人直升机的部件。用于无人机的起飞和降落，是整机不可或缺的部分。尾管通过连接结构与机身框架相连，斜撑杆用于辅助支撑尾管，起到加强固定尾管的作用。喷杆用于承载雾化器，是植保无人直升机施药装备的关键部件。由于与机身连接的发动机无法拆卸，且考虑到仿真分析与模态试验的一致性，在建立有限元模型时，采用集中质量法将发动机简化为几何模型添加到机架模型中，如图1所示。喷杆与机架的连接示意图如图2所示。通过具有弧形轨道的连接件，可以实现喷杆的自由收起与展开，机身的振动激励通过机体与喷杆的连接点传递给喷杆，从而引起喷杆的振动响应。

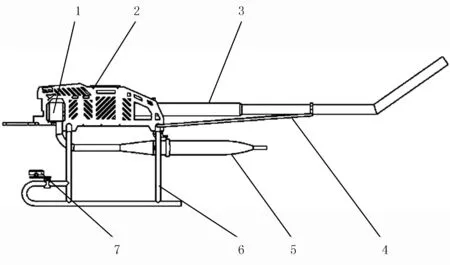
1.发动机 2.机身框架 3.尾管 4.斜支撑 5.排气管 6.起落架 7.喷杆

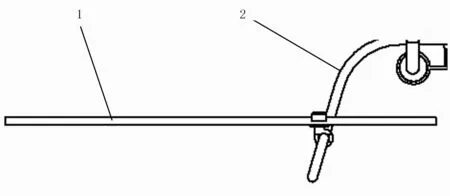
1.喷杆 2.起落架

2 油动植保无人直升机机架模态分析前处理

2.1 机架有限元模型建立

因Pro/E与有限元分析软件ANSYS Workbench具有良好的兼容性[20]，所以本研究使用Pro/E软件根据机架的实际尺寸建立机架三维模型。由于与机身连接的发动机无法拆卸，考虑到仿真分析与模态试验的一致性，在建立模型时，采用集中质量法将发动机简化为几何模型添加到机架模型中，如图3所示。将Pro/E中机架模型另存为.igs文件格式导入到ANSYS中，类型为实体。

图3 某型油动植保无人直升机机架模型图

2.2 定义模型材料属性及网格划分

将模型导入ANSYS后，定义模型的材料属性。为了满足无人机轻量的要求，机架结构中除了尾管与斜支撑是碳纤维材质外，其余部分均为铝合金材质。因在工程数据库基本材料列表中无碳纤维相关参数，所以首先将碳纤维材料属性值添加到材料库中，再为模型添加材料属性。对于本文的研究对象，定义尾管与斜支撑密度ρ为1.8×103kg/m3，弹性模量E为3.5×105MPa，泊松比μ为0.307；定义机架其余部分铝合金材料密度ρ为2.77×103kg/m3，弹性模量E为7.1×104MPa，泊松比μ为0.33。定义材料属性后，对机架有限元模型进行自由网格划分，单元大小为10mm。图4为机架有限元网格划分模型。

图4 机架有限元网格划分模型

3 油动植保无人直升机机架模态分析与计算结果

3.1 机架模态提取方法与求解

模态分析实际上就是特征值和特征向量的求解，特征值即为固有频率，特征向量为振型。无阻尼模态分析就是特征值的求解，动力学运动方程为

[M]{x//}+[K]{x}={0}

(1)

结构的自由振动为简谐振动，所以位移即为正弦函数，即

x=xsin(ωt)

(2)

将式(2)代入式(1)可得

([K]-ω2[M]){x}={0}

(3)

本文采用ANSYS Workbench程序自动控制类型模态求解器进行机架模型特征值和特征向量的求解。机架的自由振动可以表示为各阶固有频率的线性组合，其低阶固有频率较高阶固有频率对机架结构的振动影响大[22]，所以提取机架模型在自由状态下前8阶非刚体模态。

3.2 机架模态计算结果分析

经过计算，得到机架模型在自由状态下前8阶非刚体模态固有频率及振型。第1阶固有频率是15.901Hz，振型主要表现为两根喷杆上下对称摆动；第2阶固有频率是20.218Hz，振型主要表现为两根喷杆进行上下平行摆动，同时机体左右摆动；第3阶固有频率是21.665Hz，振型主要表现为两根喷杆前后对称摆动；第4阶固有频率是22.607Hz，振型主要表现为两根喷杆前后平行摆动，同时机体左右摆动；第5阶固有频率是39.869Hz，振型主要表现为机体两侧前后交替扭摆，喷杆随之前后摆动；第6阶固有频率是45.239Hz，振型主要表现为机体两侧同时向里向外扭摆，喷杆随之前后斜向上下对称摆动；第7阶固有频率是52.281Hz，振型主要表现为机体两侧沿前后、左右两方向同时对称扭摆，喷杆随之前后摆动，尾管开始上下摆动；第8阶固有频率是58.867Hz，振型主要表现为机体两侧前后交替摆动同时机体左右扭摆，喷杆随之前后平行摆动。

通过对前8阶非刚体模态固有频率及振型的分析可以得出：机架模型的振型变化是由单向向多向转变的，随着频率值的增长振型变化越来越复杂，由第1阶到第4阶机体及喷杆简单的单向摆动逐渐转变为第5阶到第8阶机体多向同时的扭摆，尤其在7阶、8阶模态振型扭摆越来越严重。同时，也可得出变形最大的部位在喷杆、起落架与尾管处，所以为了加强稳定性更要避免喷杆与机体发生共振。但要注意，机架模态分析结果的位移值是一个相对量，它表征各点在某一阶固有频率上振动量的相对比值，并不是绝对数值，仅反映在该阶固有频率上振动的传递情况[23]，具体幅值变化还要后续进行谐响应分析求得。图5 所示为机架模型在自由状态下前8阶中1、2、7、8阶非刚体模态振型云图。

(a) 1阶振型

(b) 2阶振型

(d) 8阶振型

4 油动植保无人直升机机架模型试验验证

4.1 机架模态试验

考虑到数值模型的可靠性常常不能保证，故采用试验模态分析技术对所建立机架有限元模型的准确性进行检验[24]。为了保证机架在激励作用下能够实现自由状态的振动，设计并制作试验台，用两根弹性较好的弹簧将机架悬挂在试验台上，保证给机架一个激励时弹簧不会抑制机架的振动，从而实现机架在自由状态下的振动。本文使用的是m+p Smart Office 数据采集与分析系统，采用锤击法-移动传感器法对机架模态信息进行采集，模态试验现场及试验系统示意图如图6所示。

1.试验台 2.机架 3.电缆线 4.信号分析仪 5.数据分析软件 6.传感器 7.力锤

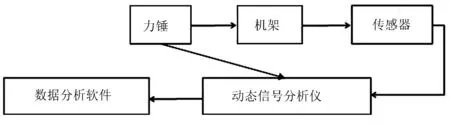
(b) 模态试验系统示意图

将机架悬挂在试验台上，选择机体框架侧板的一点为原点(0,0,0)，机架模型原点示意图如图7所示。因为机架的结构复杂，在有些位置不易粘贴传感器，在保证完整表达整机形状的前提下，各拾振点位置应均匀分布且涵盖所有结构关联点[25]，简化模型的坐标数量，参照坐标原点共确定24个空间坐标，包括23个传感器拾振点(机体框架每个侧板选取5个点、起落架共选4个点、两根喷杆各取3个点、尾管选取3个点)及1个激励点，依次连接各点定义线、定义面之后，完成在SO Analyzer中机架模型的建立。机架测试模型和测点布置情况如图8所示。模型建立完成后，设置试验参数，进行试验操作，在试验初期进行激励点的选取试验，预先选择5个激励点并依次进行锤击操作，经过多次试验后根据采集的频率数据最终选择机体框架侧板的一点为试验的敲击点。

在模态试验过程中使用DYTRAN-5800B4型力锤敲击机架侧板锤击点给出激振信号，由DYTRAN-3273A2型加速度传感器采集振动响应输出信号，依次移动传感器至每个拾振点，直到23个拾振点的信号全部采集完毕。在m+p-Vibpilot型动态信号分析仪中对采集到的输入激励信号及输出响应信号进行处理后得到频响函数，再通过Analyzer数据分析软件进行拟合分析，可以直观地获得机架结构的模态参数。

图7 机架模态试验模型原点示意图

图8 机架测试模型和测点布置

4.2 试验模态与解析模态对比验证

基于机架模态试验结果，采用模态频率差和模态置信准则判定机架有限元模型的准确性。

4.2.1 频率相关性计算

为检验有限元模型的可靠性，首先应用模态频率差以衡量有限元模型和试验模态分析模型的频率相关性[26]。用式(4)计算，结果如表1所示。

表1 试验模态与解析模态的模态频率差

续表1

(4)

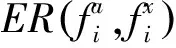
4.2.2 振型相关性计算

应用模态置信准则衡量了两者的振型相关性[27],用式(5)计算。为了简化计算过程，模态置信准则的计算过程只选择了有限元模型与试验模型模态阶数相同的前8阶非刚体模态振型进行分析，结果如表2所示。

(5)

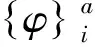
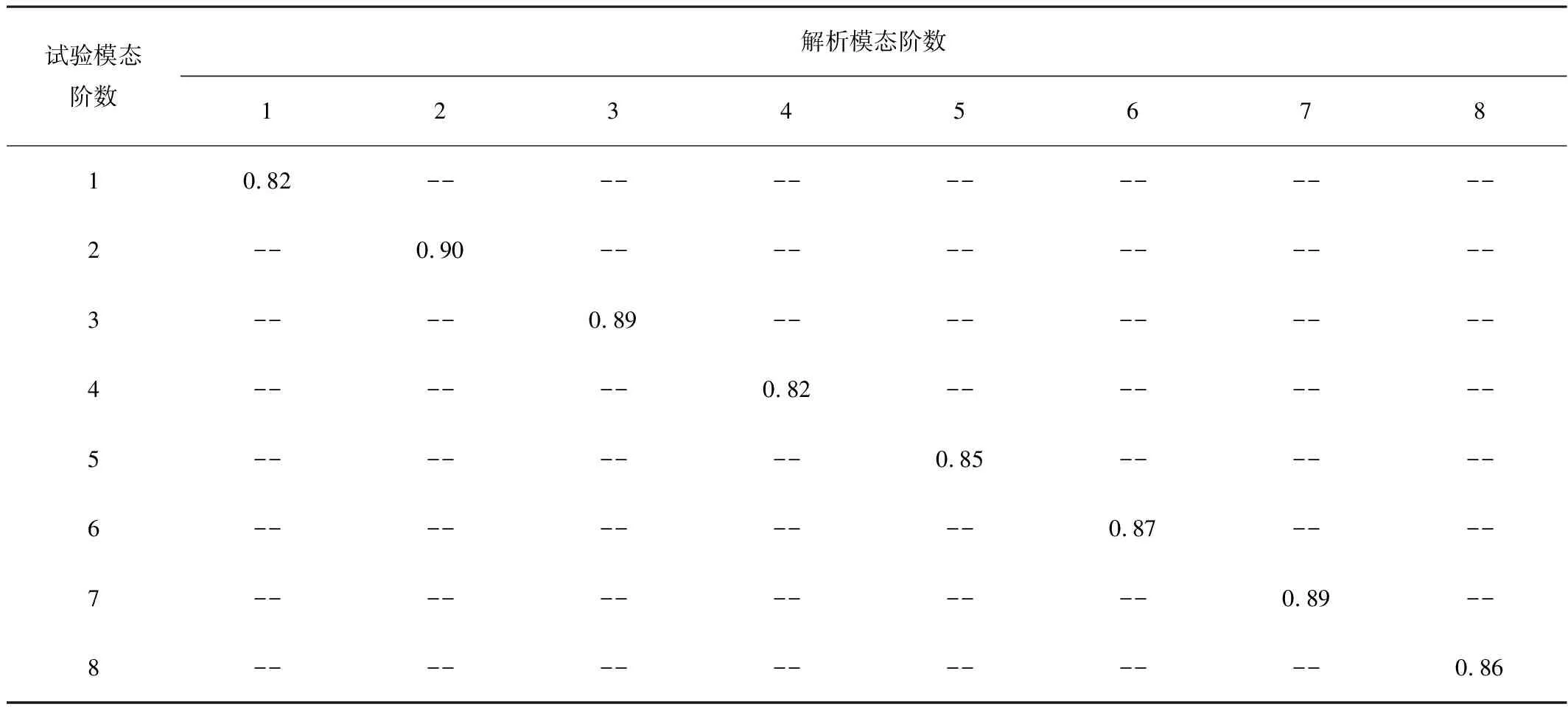
表2 模态置信准则

4.2.3 频率和振型相关性分析

通过比较分析，试验模态与解析模态的模态频率差均小于10%，满足工程要求；振型的模态置信准则都大于0.8，符合工程参考要求[28]。从数据中可以看出：机架解析模态的频率几乎都略大于试验模态的频率，这是由于建立机架有限元模型时，省略部分非承载件，忽略较小的工艺孔和倒角等对整体力学性能影响较小的几何特征[29]，模型质量小于机架实际质量，导致固有频率有所提高。对比表明：试验与解析得到的频率值误差较小，二者吻合较好。通过计算反映二者振型相关性的MAC(模态置信准则)值[24]，证明试验与分析的振型向量具有一定的相关性，仿真分析符合相关理论，建立的机架有限元模型是正确的，能够反映机架的振动特性。