一种减速装置的结构优化及模态分析
2019-12-22李晓晖时维元
李晓晖,时维元
(金陵科技学院 机电工程学院,南京 210069)
0 引言
随着我国农业机械智能化的发展,其各部件的配置也不断提高。因此,针对广泛应用于农业设备各类伺服电机、步进电机等传动系统的减速装置展开研究必不可少。根据机械设计中传动比理论,当前国内外较为成熟的减速装置可大致分为圆柱齿轮、蜗轮、行星齿轮及摆线针轮、谐波减速装置等。近年来,针对减速装置的改进,国内外学者从提高转矩、接触分析、结构参数化分析及误差分析等方面均做出不同深度试验与研究,图1为本项目拟研究的减速装置外形简图。笔者在借鉴减速装置长期工作实践与试验成果基础上,主要阐述行星齿轮减速装置结构的优化与材质最终匹配选择,以期设计出结构紧凑、性能优越的减速装置,更好地发挥农业装备的整体工作水平。
1 减速装置工作原理
减速装置作为一种相对精密的机械,被应用于各类农用工作机上,用于实现相邻运动部件的速度匹配与合理进行转矩传递。行星齿轮减速装置的主要构成部件包括传动齿轮、轴、轴承、箱体及相关附件等,如图2所示。其工作原理可简要描述为:当给定动力,减速组件太阳轮转动,可带动与其紧密连接的行星齿轮组自转,同时依靠固定在齿轮箱壳体上的内齿环沿环形轨迹进行公转;此时的行星轮组便将动力输出至与其相连接的下一传动部件,实现动力输出。这一过程的传动比调整范围由整个行星齿轮系各主、从动轮的齿数与模数等相关结构设计参数决定。

图1 减速装置外形图

1.内齿环 2.太阳轮 3.行星齿轮组
为提升减速装置的寿命及使用性能,减速装置箱体采用球墨铸铁,各内部工作齿轮采用渗碳淬火处理,拟设计减速装置的核心技术参数如表1所示。

表1 减速装置核心技术参数
2 减速装置结构优化
2.1 理论模型
充分考虑行星齿轮减速装置系统的扭矩、转速、传动比、质量与材料等核心参数,结合图3减速装置各部件振动与噪声传递过程,可知齿轮系、轴系、轴承、齿轮箱体间主要为振荡和固体声。考虑减速装置在工作过程中不可避免的空气传声,共同构成减速系统的振动与噪声源,对其进行结构优化。鉴于此系统为复杂的非线性振动系统,简化物理参数模型,则振动理论方程为
Mx″+Cx′+Kx=f(t)
(1)
式中M—质量矩阵;
C—粘性阻尼矩阵;
K—刚度矩阵;
x—位移响应向量;
x′—速度响应向量;
x″—加速度响应向量;
f(t) —激励向量。
结合齿轮相互啮合过程中会受到扭矩及载荷、轮齿变形与啮合位置变化,产生不可忽视的啮合刚度激励,因此给出刚度激励理论模型为
(2)
式中Fi—相互啮合齿轮间的接触力;
n—相互啮合齿轮对数;
δpi—主动轮变形系数;
δgi—主动轮变形系数。
因减速装置传动过程中会因齿形或齿距偏差进而产生啮合误差激励,以齿频为基本频率给出误差激励理论模型,即
e(t)=e0+ersin(2πt/T+φ)
(3)
式中e0—误差激励基值;
er—误差激励幅值;
T—减速装置齿轮啮合周期;
φ—激励角度。

图3 减速装置各部件振动与噪声传递过程简图
2.2 减速箱体优化
减速装置的箱体为减速装置的核心部件之一,承担着固定基座及传递转矩的重要角色。图4为根据减速箱体核心尺寸与装配精度要求绘制的三维实体模型。其内部与外部激励的联合作用会引起箱体的振动,为避免减速装置中齿轮啮合过程中啮合频率与箱体固有频率发生共振,进行箱体结构优化时要充分考虑箱体承载诸多载荷及抵抗应力变形的能力。

图4 减速装置箱体三维模型图
根据传动轴作用在轴承上的径向载荷、轴向载荷对箱体进行刚度、强度分析,得出箱体最大载荷密度与夹角θ处载荷密度分别为
(4)
(5)
式中Fr—减速装置箱体径向分布载荷合力;
R—减速装置轴承座孔半径;
t—减速装置的轴承宽度;
θ—载荷力q(θ)与箱体径向载荷合力Fr的夹角。
2.3 输入轴优化
根据减速装置运动与平稳性,进行输入轴的设计,则有
(6)
式中d1—拟优化输入轴的直径;
T—轴传递的额定转矩;
[τ]—轴的许用转应力。
对减速装置各部件优化采用群体空间算法理论,运用算法进行结构优化的流程简图,如图5所示。
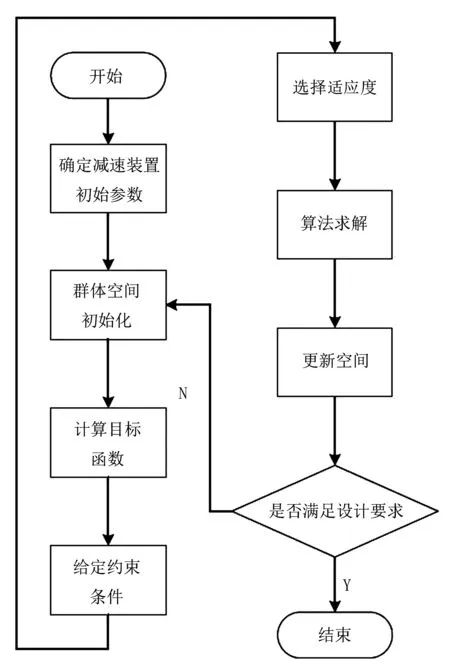
图5 减速装置优化结构算法运用流程简图
由图5可知:通过给定减速装置初始固定参数,考虑轴的弯曲强度与扭转强度,进而进行目标函数确定和约束条件限制,可达到所需机构优化目标,最终实现轴系部件的匹配。
3 模态分析
3.1 前置条件
为很好地预估优化设计的可行性,进一步对减速装置的机构动态特性进行预判断,设计减速装置模态分析硬件测试系统,如图6所示。减速装置箱体模型经施加载荷、电荷放大及传感装置到达信号采集装置,输入分析系统,数据处理后由输出设备给出所需测试参数,采用ANSYS软件对减速装置关键部件进行模态分析。

图6 减速装置模态分析硬件测试系统
3.2 试验与分析
参数确定之后,利用UG软件绘制箱体、输入轴、齿轮进行三维实体建模,并导入ANSYS试验分析软件,通过根据减速装置实际运转过程不同部件发挥作用不同,进行如下操作:
1)赋予零部件材料性能,弹性模量选择1.50e5MPa,泊松比取0.3;
2)进行有限元网格划分;
3)进行边界约束并施加载荷;
4)求解分析。
利用后续处理功能,生成减速装置输入轴的4阶振型如图7所示。由图7可知:振动较为明显区域分布在所左右轴颈部位,可求得输入轴的第1阶至第4阶固有频率分别为386.6、387.3、1 489.8、4 421.7Hz,进而根据旋转轴输入与输出的关系,得到输出轴的固有频率和振型,为进一步验证轴的随机振动响应提供依据。同时,可将固有频率转变成输入、输出轴的临界转速,方便核心参数范围的确定。生成减速装置箱体应力分布云图,如图8所示。由图8可确定应力最大值分布区域并通过许用应力与强度极限之间的关系,对安全系数进行校核,验证参数选择的合理性。

图7 减速装置输入轴的4阶振型图

图8 减速装置箱体应力分布云图
进一步对试验获得数据进行加工处理,得出如表2所示的减速装置整机优化前后1、2阶相关参数变化。由表2可知:阻尼比较结构优化前平均提高10.2%,1阶固有频率降低79Hz,2阶固有频率提高37.5Hz,有效避开结构优化前的减速装置零部件共振区。表3为减速装置整机优化模态柔度变化情况。由表3可知:减速装置的最大模态柔度由2.89×10-6rad/(N·mm)降低为2.45×10-6rad/(N·mm),模态柔度均度由3.678%降低至3.251%,表明减速装置结构优化后各阶柔度分布更均匀。
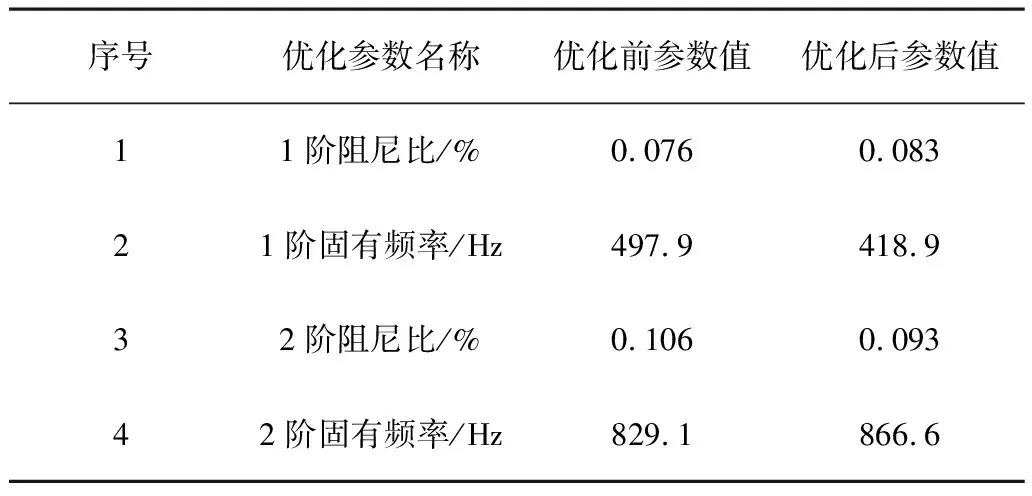
表2 减速装置优化前后试验对比
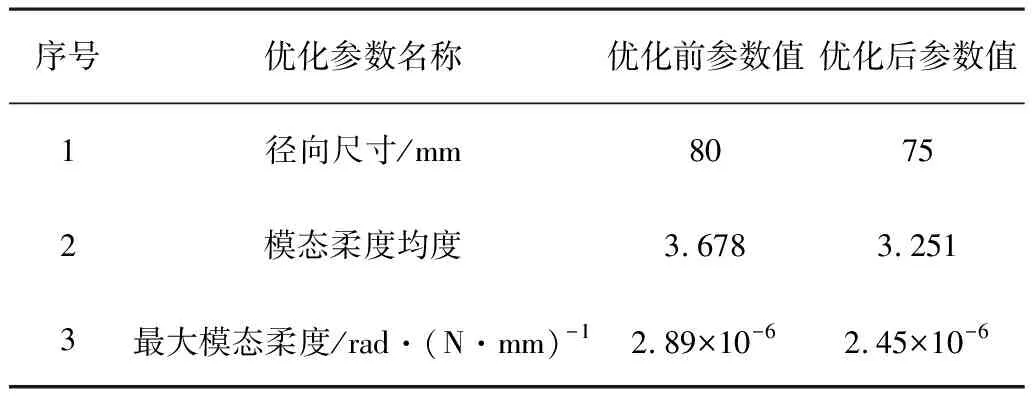
表3 减速装置优化前后性能对比
4 结论
1)在充分理解减速装置结构组成及工作原理的基础上,针对行星齿轮减速装置工作性质建立理论振动模型,进行结构参数优化。
2)利用UG软件对减速装置核心部件进行三维实体建模并通过HyperMesh软件预处理,给定相关约束条件,运用ANSYS软件进行减速装置部件模态分析,很好地将现代CAE理论有效结合,得出输入轴的4阶频率与振型图,箱体应力分布云图及可为结构优化准确避开应力集中区域提供参考。
3)通过对减速装置理论结构参数优化、模态试验分析,得出:结构优化前后的行星齿轮减速装置核心参数(如阻尼比、固有频率等)指标均有所提升,且整体模态柔度均度得到优化,验证了优化的可行性,可为其他类似减速装置结构设计提供一定思路和方法。
