钢索约束下喷杆臂的动力学行为数值模拟与试验*
2022-08-12闫军朝薛新宇宗玉郭靖胡元森许浩浩
闫军朝,薛新宇,宗玉,郭靖,胡元森,许浩浩
(1. 常州机电职业技术学院,江苏常州,213164; 2. 农业农村部南京农业机械化研究所,南京市,210014; 3. 伊犁技师培训学院,新疆伊宁,835000)
0 引言
2017年统计结果显示,在中国,喷幅在10~14.9 m的中小型喷杆喷雾机占比达70%[1]。中小型喷杆喷雾机通过钢索约束喷杆臂的大范围振荡。喷杆喷雾机田间作业时受到土壤不平整、车速变化、轮胎负载不均、药液晃动等不确定因素影响,容易导致喷杆臂产生滚转、横摆等有害运动,钢索的约束致使喷杆臂产生急停和振荡,严重影响喷雾分布形态,导致化肥农药“漏喷”和“重喷”现象发生。由于喷杆臂的不规则运动,其全面雾量分布的变异系数波动范围为0~800%(理想的雾滴沉积为100%)。喷杆臂的滚动和垂直弹性变形的影响较大,特别是在喷杆臂的末端,在喷杆运动幅度最大的情况下,最大沉积量达到760%,最小沉积量为0[2-4]。喷杆喷雾机是复杂的多体系统,建立钢索约束下的喷杆臂精确运动模型对探索其振动控制方法具有重要意义。
当前对喷杆臂动态响应的研究多集中在大型桁架式喷杆臂上[5-10]。对钢索约束下喷杆臂的动态响应研究较少,钢索约束下喷杆臂的动态响应属于非线性动力学行为。目前,用于求解钢索约束下喷杆臂非线性动力学问题的理论分析方法主要有数值求解法和解析求解法[11-13]。本文采用解析求解法中的分段线性法,通过传递函数将钢索约束下的喷杆臂运动进行非线性分段,在各段中求解线性方程,并利用两段间的边界协调条件将各段的解联系起来,从而得到喷杆臂碰撞振动问题的解析解。该方法时域变换形式简单,使解算进一步简便,并与试验结果进行比较。
1 钢索约束下喷杆臂振动模型
受钢索约束喷杆臂的振动过程如图1、图2所示。以喷杆喷雾机静止时的平衡位置为零点,取铅垂坐标轴向上为正。当喷雾机在田间行走作业时遇到障碍物,障碍物给喷雾机施加一个阶跃载荷激励u(t),由于惯性作用,喷杆臂末端向下振动。当喷杆臂末端由平衡位置0向下振动时,受到钢索的限位约束,产生碰撞,直至喷杆臂向下振动到最低位置1处,随后向上振动。当喷杆臂末端向上越过水平位置0时,钢索处于松弛状态,喷杆臂末端向上最高振动位置2处,随后,喷杆臂末端由位置2向下振动时,当喷杆臂到达平衡位置0时,受到钢索的限位约束,产生碰撞。由于钢索上端固定在喷杆悬架上,由于喷杆悬架各零部件间存在运动间隙,所以造成喷杆臂向下振动时可以越过钢索限制的平衡位置继续下行,直至喷杆悬架各零部件间的间隙消除,喷杆臂达到最低振动位置,在此过程中,喷杆臂受到钢索向上的阻力,直至喷杆臂向下振动到最低位置1处。随后反弹,重复上述振动。
根据钢索约束下喷杆臂振动特点,取单边喷杆臂CD段进行研究。在整个振动过程中,将喷杆悬架和钢索作为系统A,喷杆臂作为另一个系统B。整个振动过程由2个振动响应状态构成。
喷杆臂末端从平衡位置向下振动,钢索约束喷杆臂向下振动,直至喷杆臂末端到最低位置。随后,喷杆臂从最低位置向上振动,钢索收缩速度低于喷杆臂的反弹速度,假设此时钢索不给喷杆臂施加拉力。并返回到平衡位置,即钢索约束喷杆臂振动状态。

图1 喷雾机及喷杆总成Fig. 1 Sprayer body and boom assembly1.轮胎 2.喷杆臂 3.钢索 4.喷杆悬架 5.车身
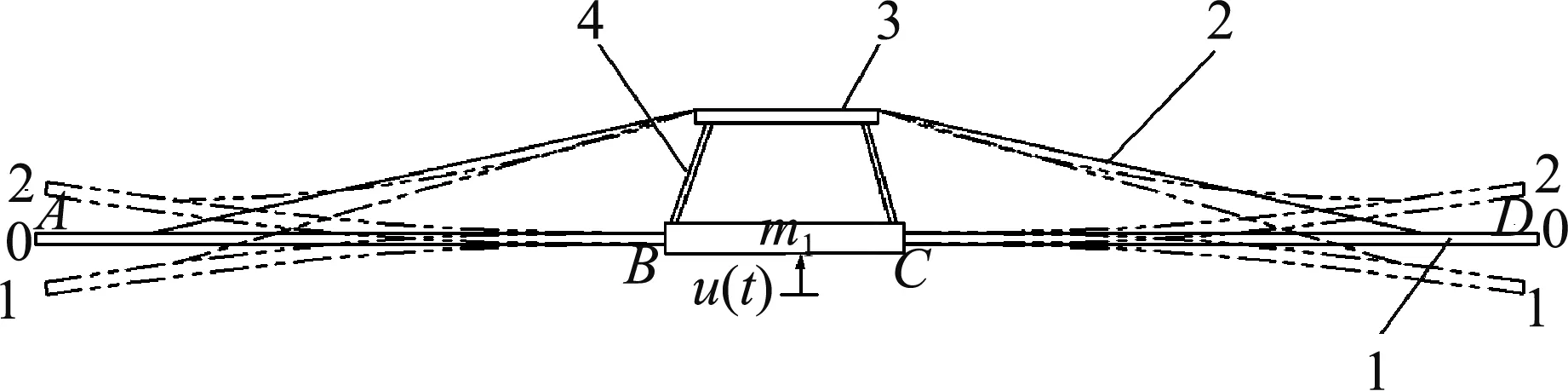
图2 钢索约束下喷杆臂振动过程Fig. 2 Process of vibration of spray boom restrained by steel cable1.喷杆臂 2.钢索 3.喷杆悬架 4.连杆
喷杆臂末端向上振动,钢索松弛,直至喷杆臂从最高位置返回平衡位置,即喷杆臂处于自由振动状态。
由于喷杆臂自由振动状态没有外力干涉,可以类比为柔性悬臂梁振动,这里不进行讨论。本文主要讨论钢索约束喷杆臂振动状态,由于钢索的约束力,导致喷杆臂振动产生强非线性和奇异现象,使喷杆臂的动态行为变得十分复杂多样。当喷杆臂由平衡位置向下振动时,钢索给喷杆臂施加阻力,当喷杆臂到达最低位置时,钢索施加在喷杆臂上的力达到最大。当喷杆臂由最低位置向上振动到平衡位置过程中,钢索给喷杆臂施加拉力,当喷杆臂到达平衡位置时,钢索拉力消失。喷杆臂由平衡位置向下振动并返回平衡位置的过程类似于给喷杆臂施加一个弹簧阻尼系统[14],见图3。

图3 钢索约束下喷杆臂振动力学模型Fig. 3 Vibration mechanics model of spray boom restrained by steel cable
以喷杆臂静止时的平衡位置为零点,取铅垂坐标轴向上为正。喷杆臂的振动方程
(1)
式中:W0(x,t)——喷杆臂运动的挠曲线;
E——喷杆臂弹性模量,Pa;
I——喷杆臂惯性矩,m4;
l——喷杆臂的长度,m;
ρ——喷杆臂的材料密度,kg/m3;
A——喷杆臂横截面积,m2;
f0(t)——喷杆臂在钢索连接处受到的垂直方向上的作用力,N;
f1——弹簧阻尼系统受到的垂直方向上的作用力,N;

弹簧阻尼系统的运动方程
(2)
式中:K1——弹簧刚度(喷杆臂悬架和升降机构的等效刚度);
c1——阻尼常数(喷杆臂悬挂和升降机构的等效阻尼);
y1(t)——弹簧阻尼系统位移;
f1(t)——弹簧阻尼系统受到的作用力。
喷杆臂在运动过程中,可能处于喷杆臂不受约束和受约束两种运动状态,应当分别满足的条件
喷杆臂自由振动状态
f0=0,f1=0,0≤w0
(3)
钢索约束喷杆臂振动状态
f0=-f1≥0,0≤w0=y1
(4)
式中:w0——喷杆臂与弹簧阻尼系统接触点处的位移。
理论分析受钢索约束喷杆臂振动系统,实质上就是求解式(1)~式(4),而分段线性法求解析解的实质则是:按不同运动接触状态的转换条件,推导出不同接触运动状态时的解析解。
1.1 喷杆臂和弹簧阻尼系统的动态特性
为了处理的方便,喷杆臂和弹簧阻尼系统的动态特性都用传递函数描述,并且统一用极点-留数格式表达,这可以通过对式(1)和式(2)进行Laplace变换得到
(5)
(6)
式中:Y0(x,s)——喷杆臂挠曲线的Laplace变换;
Y1(s)——弹簧阻尼系统位移的Laplace变换;
F0(s)——喷杆臂接触碰撞作用力的Laplace变换;
F1(s)——弹簧阻尼系统接触碰撞作用力的Laplace变换;
U(s)——阶跃激励的Laplace变换。
弹簧阻尼系统的传递函数很容易由式(6)得到。
(7)
式中:H1(s)——弹簧阻尼系统传递函数;
s1——弹簧阻尼系统极点;
r1——弹簧阻尼系统留数。
喷杆臂的传递函数需要通过对式(5)求解得到,其通解
Y0(x,s)=h·a
(8)
其中:h=[cosλxsinλxcoshλxsinhλx]T,
a=[ABCD]T,
代入边界条件得到
Ma=v
(9)
其中:v=[U(s) 0 0F(s)/λ3]T,通过式(9)的逆形式可求得Y0的通解
(10)
式中:M*——方阵M的代数余子式。
将式(10)整理成传递函数形式
Y0(x,λ)=Hu(x,λ)U(s)+HF(x,λ)F(s)
(11)

满足奇异性1+cosλcoshλ=0的λ序列的λk为一近似等差数列,-λk、-λki、+λki都满足奇异性条件。与λk对应的振型留数rU(x,λk),rF(x,λk)[15]
(12)
对式(12)进行归一化处理可以得到
rU(x,λk)=rU(1,λk)Z(x,λk),rF(x,λk)
=rF(1,λk)Z(x,λk)
(13)
式(13)中Z(x,λk)为与λk对应的归一化振型rU(x,λk)/rU(1,λk)或rF(x,λk)/rF(1,λk)。至此,便可以将传递函数HU(x,λ)、HF(x,λ)表示为极点-留数格式
(14)
留数数列rU(1,λk),rF(1,λk)参见表1,可以证明,rF(1,λk)=-rF(1,-λk),rF(1,λki)=rF(1,λk)i。
1.2 钢索约束下喷杆臂的动态响应分析
喷杆臂的动态响应分析应当有系统动态特征表达、不同接触状态的运动分析、不同接触状态之间的转换关系三部分内容,以下的讨论假定两个线性系统是不受限制的一般线性系统。
喷杆臂和弹簧阻尼系统激励响应关系可以表达
(15)
式中:F0(s)——喷杆臂在碰撞点上所受的力;
F1(s)——弹簧阻尼系统在碰撞点上所受的力;
Y1(s)——弹簧阻尼系统碰撞作用点处位移的Laplace变换;
Y0(n,s)——喷杆臂上弹簧阻尼系统碰撞点处位移的Laplace变换,弹簧阻尼系统在喷杆臂上的碰撞点在n=3l/4处;
HF(n,s)——相对应的传递函数;
H1(s)——相对应的传递函数;
Hu(n,s)——相对应的传递函数;
y0(n,s)——喷杆臂位移响应Laplace变换中的初值响应部分;
y1(s)——弹簧阻尼系统位移响应Laplace变换中的初值响应部分;
U(s)——阶跃激励。
为了分析方便将传递函数表示成极点-留数格式
(16)
式中:s0(k)、s1(k)——传递函数极点序列;
rF(k)、r1(k)、ru(k)——传递函数留数序列;
N0、N1——极点数目;
Z(n,k)——喷杆臂k阶极点的振型。
这里暂不考虑无穷多极点和重极点问题。
喷杆臂的运动有悬空和下接触状态,其运动状态的描述、求解及状态转换分别讨论如下。
1.2.1 喷杆臂悬空状态分析
喷杆臂处于悬空时接触力为0,喷杆臂和弹簧阻尼系统的位移响应可以表示为自由响应和激励响应之和
(17)
式中:A0(k)、A1(k)——与极点对应的自由响应幅值;
Aω——激励响应幅值;
sω——激励的留数,sω=iω;
ω——指激励的频率,此后的公式中sω和ω的意义相同。
时域响应
(18)
1.2.2 喷杆臂由悬空状态向接触状态转换
当喷杆臂由自由振动状态向下与弹簧阻尼系统接触及处于接触状态时,喷杆臂和弹簧阻尼系统应满足条件
(19)
或Laplace变换
(20)
代入式(15)可以求得F0(s)和Y0(s)
F0(s)=-F1(s)
(21)
式中:δ——喷杆臂处于最高位置时,碰撞点与弹簧阻尼系统之间的距离。
F0(s)和Y0(s)也都可以写为与弹簧阻尼系统接触状态时极点-留数格式
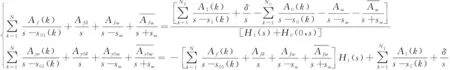
(22)
式中:s01(k)——喷杆臂处于与弹簧阻尼系统接触状态时系统的极点,也就是H1(s)+H0(s)的零点;
Af(k)、Afδ、Afω——F0(s)与极点、距离、激励对应的响应幅值;
Ayo(k)、Ay0δ、Ay0ω——Y0(s)与极点、距离、激励对应的响应幅值。
式(22)等号两边分别同乘以s-s01(k)、s、s-sω。并取极限可求得
(23)
式(23)就是喷杆臂由悬空运动到向下与弹簧阻尼系统接触运动的状态转换关系。其时域响应
(24)
1.2.3 喷杆臂由接触状态向悬空状态转换
喷杆臂向上振动脱离弹簧阻尼系统时接触力数值为0,其后的响应可以通过在接触状态的响应中减去接触力引起的响应部分而得到
H0(s)
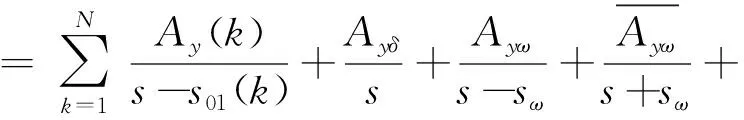
(25)
式(25)第一式等号两边分别同乘以s-s0(k)、s-iω,第二式等号两边分别同乘以s-s0(k),取极限可求得喷杆臂与弹簧阻尼系统由接触进入悬空状态的Ao(k)、A1(k)、Aδ
(26)
2 钢索约束下喷杆臂动态响应模拟及验证
2.1 喷杆臂系统的极点、留数理论值
不受钢索约束时,喷杆臂的结构保持不变,喷杆臂的材料阻尼取作0.12,传递函数按式(14)截取前2阶固有频率进行计算,得到了不受间隙约束时喷杆臂系统的极点、留数序列,如表1所示。
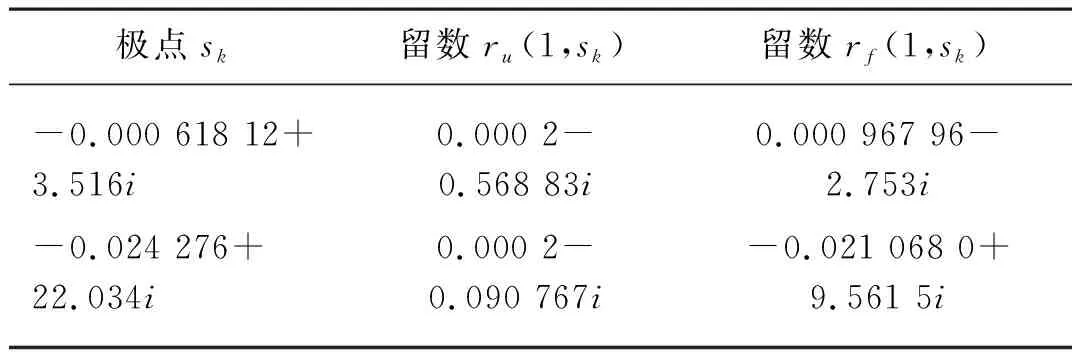
表1 喷杆臂系统的极点和留数的理论值Tab. 1 Theory dates of pole and residue of boom system
2.2 喷雾机参数确定
为了验证所提出的钢索约束下喷杆臂振动模型的正确性,选择SWAN3WP-500自走式喷杆喷雾机喷杆臂进行模型验证。SWAN3WP-500自走式喷杆喷雾机喷杆臂喷幅为10 m,单边喷杆臂从车身向外延伸长度为3.5 m。喷杆臂的材料为铝合金6063-T5,横截面结构有2种,如图4所示。喷杆臂工作时,横截面长边垂直,短边水平。本次仿真及实验所用喷杆臂的横截面结构为A型。其相关参数如表2所示。
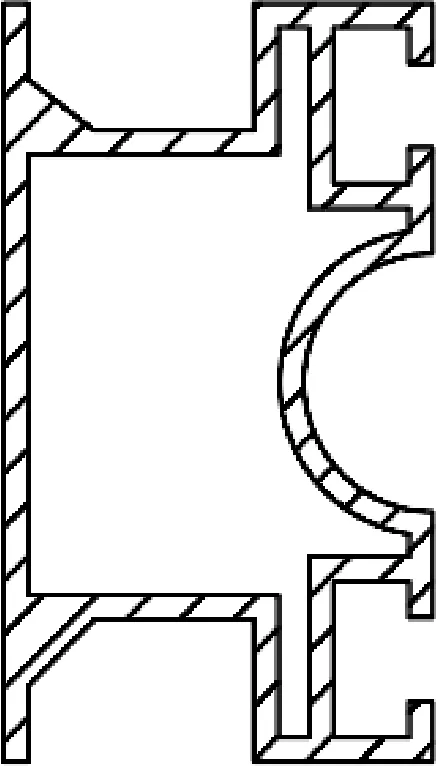
(a) A型
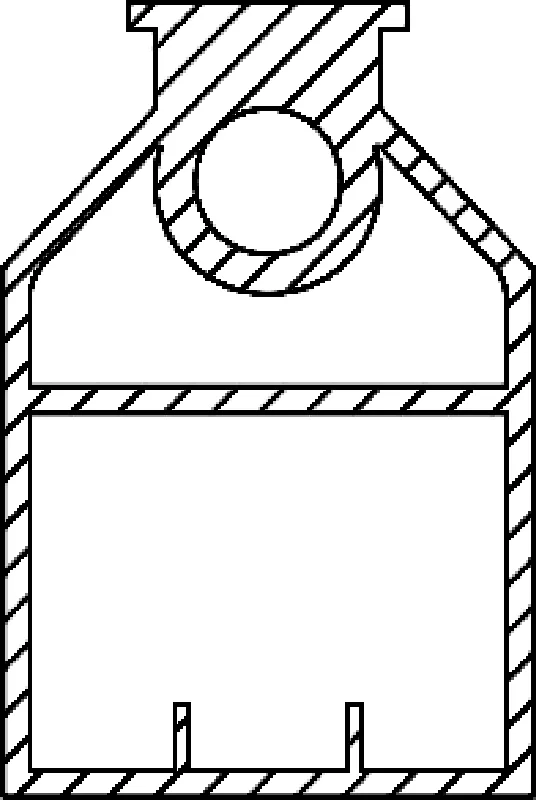
(b) B型图4 杆臂横截面结构Fig. 4 Cross-sectional structure of the spray boom

表2 喷杆臂参数表Tab. 2 Main parameters of the spray boom
喷雾机在田间行走时,车轮遇到的障碍物高度或深度一般在100 mm左右,障碍物在喷雾机前进方向上的长度一般在150 mm左右。现设置100 mm、150 mm、200 mm三种幅值和5 Hz、10 Hz两种频率的阶跃激励函数。按照表1和表2设置模型相关参数,以第2节建立的钢索约束下喷杆臂动力学行为模型为基础,对钢索约束喷杆臂的动力学行为进行数值仿真计算,喷杆臂动态响应仿真的流程为:首先给出初始的悬空运动状态A0(k)、A1(k),并求出Aω;依据悬空响应式(18)和接触发生条件式(19)判断接触,并求出悬空阶段的运动时间和悬空阶段结束时的运动状态;根据悬空向接触状态的转换关系式(22)求出接触状态的初始状态Af(k)、Afδ、Afω;依据接触力响应式(23)和接触终止条件求出接触阶段时间和接触阶段结束时的运动状态;依据接触向悬空状态的转换条件式(25)求出下一次悬空状态的初始状态Ao(k)、A1(k)、Aω;完成一次仿真后再重复(2)~(5)直到仿真结束。仿真流程如图5所示。
图6为模拟钢索约束下的喷杆臂在阶跃激励频率为10 Hz时,分别在100 mm、150 mm和200 mm三种阶跃激励幅值下的振动情况。从图中可以发现,当喷杆臂从平衡位置向下振动时,喷杆臂受到钢索的约束阻力,产生明显的多次畸变,当喷杆臂由最低位置向平衡位置,以及最高位置反弹时,曲线的畸变明显减少,表明,在此过程中,喷杆臂受到的是自身变形产生的阻力。当喷杆臂由最高位置向平衡位置振动时,钢索处于松弛状态,对喷杆臂不施加约束,曲线畸变较少。另外,曲线随着激励幅值的增加,喷杆臂振动的幅度逐步增大,振动衰减的速度在减慢。

图5 仿真流程Fig. 5 Flow chart of dynamic response simulation of spray boom restrained by steel cable
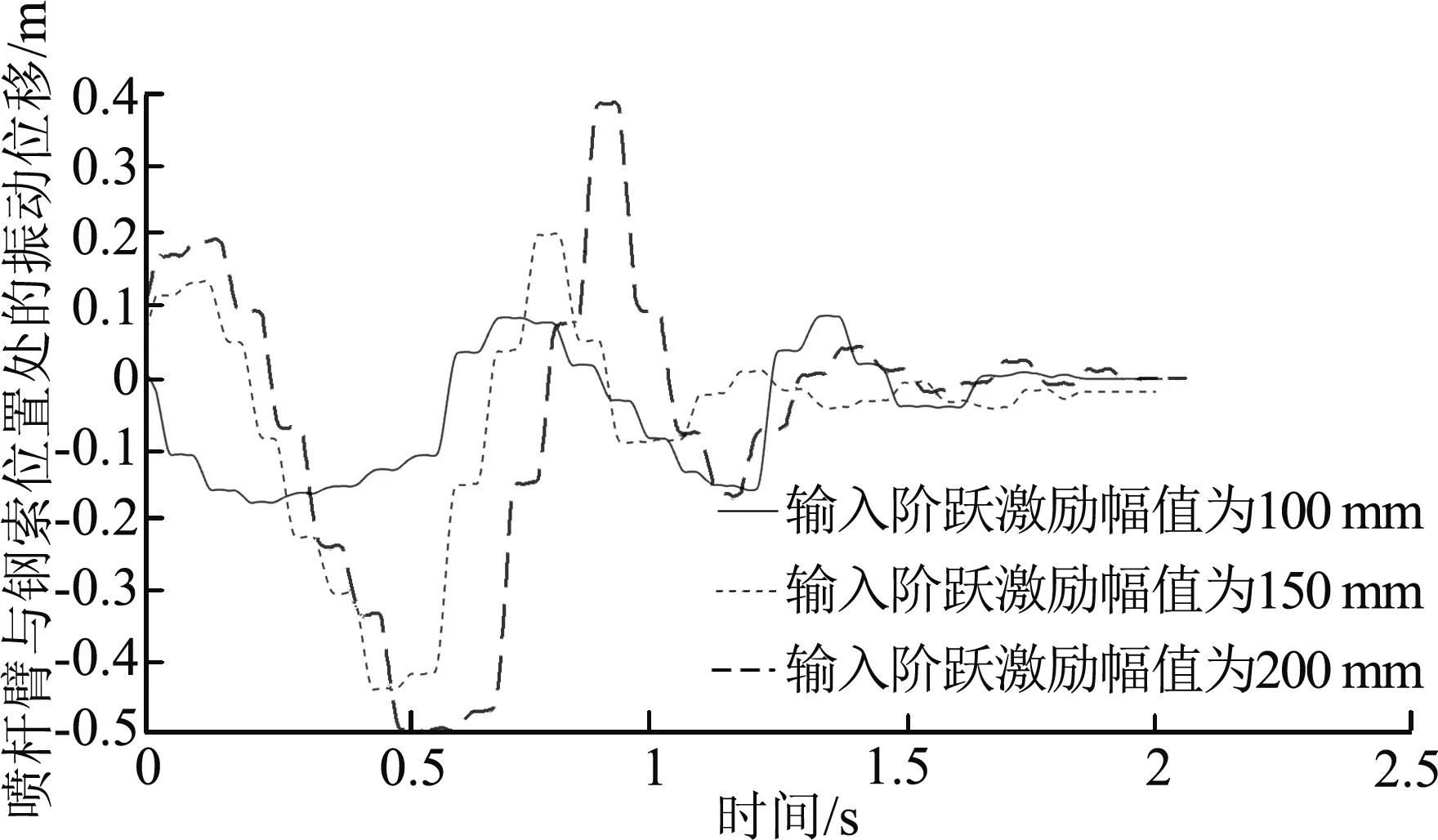
图6 模型预测三种阶跃激励幅值下喷杆臂振动情况Fig. 6 Model predicted values of the vibration of the spray boom under three step excitation amplitudes
2.3 钢索约束下喷杆臂动态响应实验
为了验证所提出的数学模型的准确性,搭建了钢索约束下的喷杆臂振动试验系统。喷杆臂安装在两个液压缸上,液压缸控制系统向液压缸输出阶跃激励信号。本试验信号采集系统采用DH5902测试采集系统和Q45u系列超声波传感器和50 g单轴加速度传感器,Q45u系列超声波传感器有效检测距离为0.25~3.0 m,工作温度范围为-25 ℃~+70 ℃,采样上限频率为100 Hz,灵敏度为100 mV/V。Q45u系列超声波传感器和50 g单轴加速度传感器固定安装在喷杆臂上钢索连接处,超声波传感器由DH5902测试采集系统提供电源并接受其采集的数据,超声波传感器和加速度传感器实时记录钢索约束下的喷杆臂的振动响应情况,喷杆臂振动响应数据最终由计算机上的DHDAS动态信号采集分析系统接受和储存。
在钢索约束下的喷杆臂振动试验系统上获得了60组喷杆臂振动响应数据。测试得到的有效数据时长均在2.5 s以内,图7、图8和图9分别是喷杆臂在三种阶跃激励幅值下钢索连接处的典型振动响应曲线。可以发现,当阶跃激励幅值相同时,喷杆臂的振动幅度随着频率的增加而减小,进一步证明喷杆臂易受低频冲击影响,隔离高频冲击的性能。
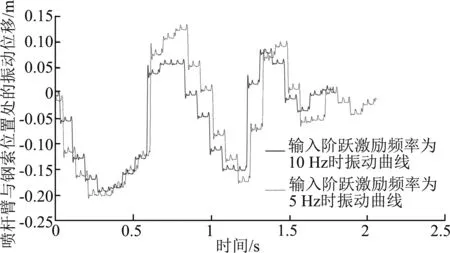
图7 阶跃激励幅值为100 mm时喷杆臂振动情况Fig. 7 Vibration of spray boom when step excitation amplitude is 100 mm

图8 阶跃激励幅值为150 mm时喷杆臂振动情况Fig. 8 Vibration of spray boom when step excitation amplitude is 150 mm
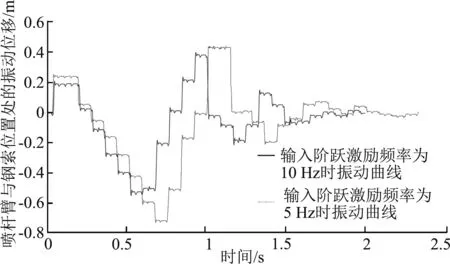
图9 阶跃激励幅值为200 mm时喷杆臂振动情况Fig. 9 Vibration of spray boom when step excitation amplitude is 200 mm
从图7、图8和图9中可以发现,当喷杆臂从平衡位置向下振动时,喷杆臂受到钢索的约束阻力,产生多次急停震荡,当喷杆臂由最低位置向平衡位置,以及最高位置反弹时,喷杆臂的急停震荡很少,在此过程中,喷杆臂受到的是自身变形产生的阻力。当喷杆臂由最高位置向平衡位置振动时,钢索处于松弛状态,对喷杆臂不施加约束,曲线畸变较少。
2.4 钢索约束下喷杆臂动态响应模型验证
图10~图12是喷杆臂分别在100 mm,150 mm和200 mm三种阶跃激励幅值下经过障碍物时实测喷杆臂钢索连接处振动响应和所建模型预测结果的对比图。

图10 阶跃激励幅值为100 mm时喷杆臂钢索连接处振动响应与模拟预测结果对比Fig. 10 Comparison results of the vibration response at the steel cable connection of spray boom and the simulation prediction results when the step excitation amplitude is 100 mm
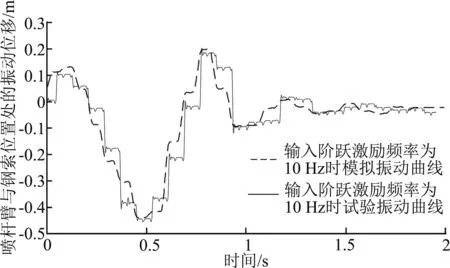
图11 阶跃激励幅值为150 mm时喷杆臂钢索连接处振动响应与模拟预测结果对比Fig. 11 Comparison results of the vibration response at the steel cable connection of spray boom and the simulation prediction results when the step excitation amplitude is 150 mm
三种激励幅值下模型仿真结果与实测结果的相关系数最小值为阶跃激励幅值为200 mm时的0.910 4。可以发现,实测喷杆臂钢索连接处振动波形畸变波形较多,且较明显,每个波峰和波谷均出现了明显的摩擦削顶现象,模型预测曲线波形具有畸变趋势,每个波峰和波谷均出现摩擦削顶趋势。实测喷杆臂振动波形较模型预测波形,在振动后期有周期变大的趋势。造成这些区别的主要原因是实测喷杆臂在经受阶跃激励驱动时,各相关部件间存在无法预测的随机碰撞摩擦。模型预测与实测值的最大误差分别出现在阶跃激励幅值为100 mm时向上的振动和阶跃激励幅值为200 mm时向下的振动,向上的误差为0.047 3 m,向下的误差为0.058 2 m,均在合理范围内。模型可以有效预测钢索约束下喷杆臂振动情况。
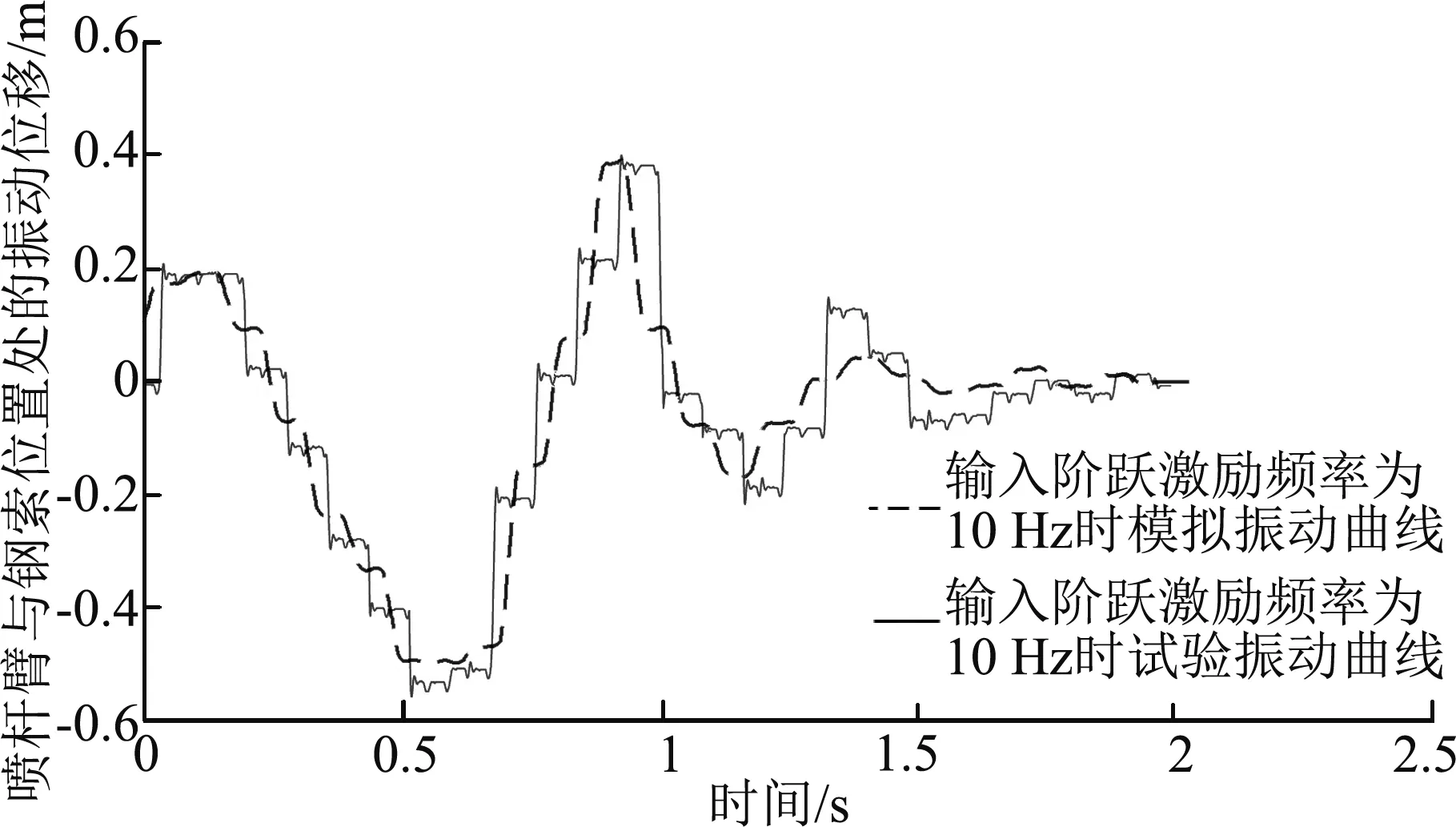
图12 阶跃激励幅值为200 mm时喷杆臂钢索连接处振动响应与模拟预测结果对比Fig. 12 Comparison results of the vibration response at the steel cable connection of spray boom and the simulation prediction results when the step excitation amplitude is 200 mm
3 结论
1) 建立钢索约束的下喷杆臂动态响应理论模型,并搭建了钢索约束下的喷杆臂振动试验系统,分别在100 mm、150 mm、200 mm等三种激励幅值下模型仿真结果与实测结果的相关系数最小值为阶跃激励幅值为200 mm时的0.910 4。模型预测与实测值的最大误差分别出现在阶跃激励幅值为100 mm时向上的振动和阶跃激励幅值为200 mm时向下的振动,向上的误差为0.047 3 m,向下的误差为0.058 2 m,均在合理范围内。验证了所提出的钢索约束的下喷杆臂动态响应理论模型的准确性。
2) 分析喷杆臂在不同阶跃激励幅值和不同阶跃激励频率下的振动情况,结果表明钢索对由平衡位置向下振动的喷杆臂有明显约束,导致喷杆臂在由平衡位置向下振动过程中有短暂急停振荡现象,进一步增加了喷杆臂的振动。随着阶跃激励频率的增大,喷杆臂钢索连接处振动的幅度和周期均减小。随着阶跃激励幅值的增大,喷杆臂钢索连接处的振动幅值和周期均增大。
