基于类桁架的多工况下平面Prager结构拓扑优化

谢汩 周克民

摘要：为开展多工况下曲面结构的拓扑优化，采用两向正交类桁架连续体材料模型和有限元分析方法，以杆件在结点位置的密度和方向为优化设计变量进行结构优化。根据有限元分析结果，采用满应力准则法优化各单一工况下的材料分布。按照多工况与各单工况下材料的方向刚度最大值的差值最小为原则，优化多工况下的杆件方向和密度分布。将杆件竖直位置的质心连线作为拓扑优化的平面Prager结构，以3个算例表明该方法的有效性。

关键词：拓扑优化; 类桁架结构; 多工况; 壳体结构; Prager结构

中图分类号：TU323.4; TP319.99

文献标志码：A

Topology optimization of Prager structure under

multiple cases based on truss-like structure

XIE Gu1， ZHOU Kemin2

（

1. Xiamen Xiangan Airport Investment Construction Co.， Ltd.， Xiamen 361006， Fujian， China;

2. College of Civil Engineering， Huaqiao University， Xiamen 361021，Fujian， China）

Abstract：

To promote the topology optimization of curved surface structures under multiple cases， the material model of two-direction orthogonality truss-like continua and the finite element analysis method are selected， and the structure is optimized by taking rod density and rod direction at node position as optimization design variables. According to the results of finite element analysis， the material distribution under

each case is optimized using the full stress criterion method. On the basis of minimum difference of material maximum directional stiffness between multiplecases and each case， the rod direction and density distributions under multiple cases are optimized. The mass centres of vertical position rods are connected to form the planar Prager structure for topology optimization. The effectiveness of the proposed method is indicated by three examples.

Key words：

topology optimization; truss-like structure; multiple cases; shell structure; Prager structure

收稿日期：2019-03-21

修回日期：2019-05-18

基金项目：

国家自然科学基金（11172106， 10872072）

作者简介：

谢汩（1981—），男，湖南宁乡人，研究方向为工程技术与结构优化，（E-mail）xiemi88@foxmail.com

0 引 言

空间壳体结构一直备受关注，其以受力合理、质量轻、结构刚度大等特点在现代建筑中得到广泛应用。在绿色环保成为全球热点的背景下，对空间壳体结构进行优化设计成为关注的焦点，其重点是确定合理的结构外形和合理的刚度分布。[1]与截面尺 寸和形状优化比较，壳体结构的拓扑优化相对较困难。[2-4]Prager结构是一种特殊的拓扑优化壳结构，其结构外形为覆盖在设计平面上一定区域的曲面。[5-7]壳体结构在该区域边界支撑，载荷沿同一竖直方向，受力点平面位置不变，竖直位置随结构变化而变化。这符合一般大跨空间壳体结构的受力特点，因此可以通过Prager结构进行壳体结构的拓扑优化。

ROZVANY等[5]在给定的竖向载荷和边界支撑条件下，建立由垂直拱梁组成的网格式曲壳模型，推导出Prager结构拓扑优化的差分迭代方程。采用差分方法时，假设杆件位于相互平行或垂直的平面內，因此杆件方向不能优化，只能分析简单载荷情况。Prager的结构形式随载荷变化而变化，因而与常规结构优化问题[8-9]有较大区别。本文采用类桁架材料模型[10-12]和有限元分析方法，解决具有复杂载荷条件和边界条件等更一般的优化问题，且为计算简单仅研究多工况竖向载荷下的平面Prager结构。

1 类桁架连续体材料模型

假设设计域内任一点都有2组正交的杆件分布，并假设这2个正交方向为材料主轴方向，按这2个材料主轴方向建立局部坐标系。

1.1 弹性矩阵

假定这2个材料主轴方向的杆件分布密度分别为t1和t2，弹性模量为E。为避免刚度矩阵奇异，并使材料在t1=t2时各向同性，设剪切等效密度为（t1+ t2）/4。由于平行桿件之间没有作用力，所以假设横向变形因数为0。材料主轴方向的弹性矩阵为

D（t1，t2，0）=E

t1t2（t1+t2）/4

（1）

假设材料主轴坐标系与整体坐标系xOy的夹角为α，则整体坐标系下的弹性矩阵为

D（t1，t2，α）=

TT（α）D（t1，t2，0）

T（α）

（2）

式中：T（α）为应变转换矩阵。式（2）还可以写为

D（t1，t2，α）=

Etm

1+Rtcos 2α00.5Rtsin 2α

01-Rtcos 2α0.5Rtsin 2α

0.5Rtsin 2α0.5Rtsin 2α0.5

（3）

式中：tm=（t1+t2）/2，Rt=（t1-t2）/（t1+t2）。

1.2 多工况下模型参数的确定

在多工况优化中，材料各结点处可能不止有2组杆件，也可能不互相垂直。为使问题简化，仍然采用正交材料模型。将式（3）中第1行第1列元素展开可得

D11 （t1，t2，α）=E（（t1+t2）+（t1-t2）cos 2α）/2

（4）

式（4）为材料在x方向产生单位变形时的应力，反映该方向的刚度。假设在任意单工况l（l=1，2，…，L）下的拓扑优化结果中，材料沿αl和αl+π/2方向分别布置有密度为t1，l 和t2，l 的正交杆件，此时材料在任意θ方向的刚度为

D11 （θ;t1，l ，t2，l ，αl）=

E（（t1，l +t2，l ）+（t1，l -t2，l ）cos 2（αl-θ））/2

（5）

在所有单工况下，方向刚度的最大值

Sm（θ）=max l=1，2，…，LD11 （θ;t1，l ，t2，l ，αl）

（6）

式（6）为所有工况下各方向刚度的包络线。如果在多工况下φ和φ+π/2方向布置有密度为x1和x2的梁，则方向刚度D11 （θ;x1，x2，φ）可以写为

D11 （θ;x1，x2，φ）=

E（（x1+x2）+（x1-x2）cos 2（φ-θ））/2

（7）

用2-范数定义式（6）和（7）的差值为

δ2≡∫π 0 （D11 （θ;x1，x2，φ）-Sm（θ））2dθ=

∫π 0 （D11 （θ;x1，x2，φ））2dθ-

2∫π 0 D11 （θ;x1，x2，φ）×

Sm（θ）dθ+∫π 0 （Sm（θ））2dθ

（8）

其中：∫π 0 （Sm（θ））2dθ只受各单工况下优化材料的分布参数t1，l 、t2，l 和αl的控制，与多工况下的设计变量x1、x2和φ无关。将式（8）前两项记为δ21，积分可得

δ21=

πE2（2（x1+x2）2+（x1-x2）2）/8-πE2（（x1+

x2）I0+（x1-x2）（I1cos 2φ+I2sin 2φ））

（9）

其中：

（I0，I1，I2）=

1πE

∫π 0 Sm（θ）（1，cos 2θ，sin 2θ）dθ

（10）

为优化结构材料，使多工况下与各单工况下梁刚度的最大值接近，即使式（9）取极小值。由于

∫π 0 （Sm（θ））2dθ

与多工况下的优化变量无关，因此只需要求式（10）的极小值。对δ21关于（x1+x2）、（x1-x2）和φ分 别求偏导，得

δ21（x1+x2）=（4（x1+x2）-8I0）πE28

（11）

δ21（x1-x2）=（2（x1-x2）-8（I1cos 2φ+

I2sin 2φ））πE28（12）

δ21φ=-16（x1-x2）（-I1sin 2φ+I2cos 2φ）πE28

（13）

令式（11）和（12）等于0，联立求解得

x1，x2=I0±2（I1cos 2φ+I2sin 2φ）

（14）

令式（13）等于0，求解得

φ=φ0

φ0+π2 ， φ0=12arctanI2I1

（15）

由此使式（8）或（9）取极小值的解为

φ=

φ0，I1cos 2φ0+I2sin 2φ0≥0

φ0+π2，I1cos 2φ0+I2sin 2φ0<0

（16）

2 有限元分析

2.1 单元刚度矩阵

为编程方便，将式（2）变换为

D（t1，t2，α）=E

2b=1tb3r=1

sbr

gr（α）

（17）

其中：

gr（α）=[cos 2αsin 2α1]

（18）

sbr =111-1-11

（19）

以杆件在结点位置的密度t1，j 、t2，j 和方向αj作为设计变量，单元内部任意点（ξ，η）的弹性矩阵可由形函数

Nj（ξ，η）

插值得到，即

De（ξ，η）=E

j∈SeNj（ξ，η）

D（t1，j ，t2，j ，αj）=

E

j∈SeNj（ξ，η）

2b=1tbj

3r=1

sbr

gr （αj）

Ar

（20）

A1=12

1

-10，

A2=14001001110，

A3=121

1

1/2（21）

式中：Se为属于单元e的结点集合。

由此可以得出单元刚度矩阵为

K=

e

∫ Ve

BT

De

BdV=

Ee

j∈Se

2b=1tbj

3r=1

sbr

gr（αj）

Hejr

（22）

式中：Ve为单元e的体积;

Hejr 为常数矩阵，

Hejr =E∫Ve Nj

BT

Ar

BdV

（23）

对于将设计域划分形成的矩形单元，该常数矩阵与单元无关，可以在有限元分析前求解。同样，单元内部的杆件密度可由插值得到，因此结构体积为

V=

e

j∈Se

b

∫ Ve Njtbj dV=

e

b

j∈Se

tbj

∫ Ve NjdV=

j

bvjtbj

（24）

式中：

vj=e∈Sj∫Ve NjdV，

Sj，表示围绕结點j的单元集合。

对于将设计域划分形成的矩形单元，vj也是常数。

2.2 求解过程

基于以上推导，可将优化迭代过程归纳如下。

（1）采用有限元划分设计域。初始化设计参数，即

t0，bj =1

α0，j =0 ， b=1，2; j=1，2，…，J

（25）

式中：下标0为迭代指数;J为结点总数。

（2）利用有限元分析，得到各结点位置的主应力方向θk，j 和主应力方向的应变εk，bj 。

（3）采用满应力准则法优化杆件在结点位置的密度，将杆件方向调整到主应力方向，即

k+1，bj =Etk，bj εk，bj /σp， αk+1，j =θk，j

（26）

式中：下标k为迭代指数;σp为材料的许用应力。为避免密度过小导致刚度矩阵，限制

tk+1，bj =max（ξtk+1，m ，k+1，bj ）， tk+1，m =max b，j（k+1，bj ）

（27）

式中：ξ为常数，此处取1×10-6 。按照优化后的杆件密度分布调整载荷在竖直方向的分布。

（4）检查收敛条件，判断杆件密度在2次迭代中的相对变化量是否足够小，即

max b，jtk+1，bj -tk，bj /tk+1，m <δ （28）

式中：δ为一极小数，此处取1×10-4 。若不满足收敛条件则返回第（2）步。

（5）将杆件密度在竖直方向的质心连线，可以表示最后的拓扑结构。

3 算 例

选择3个平面问题算例，设计域为4×3，两端铰支，载荷只表示力沿水平方向的分布，不表示竖直位置。采用40×30个正方形单元，由于载荷大小、结构尺寸和材料的弹性模量E等皆与拓扑优化结果无关，所以不给出具体数据。

算例1选择文献[5]中的单工况算例进行对比，其力学模型见图1a），载荷为均布力。解析解和杆件质心连线表示的拓扑优化结果见图1b），这两者非常接近。

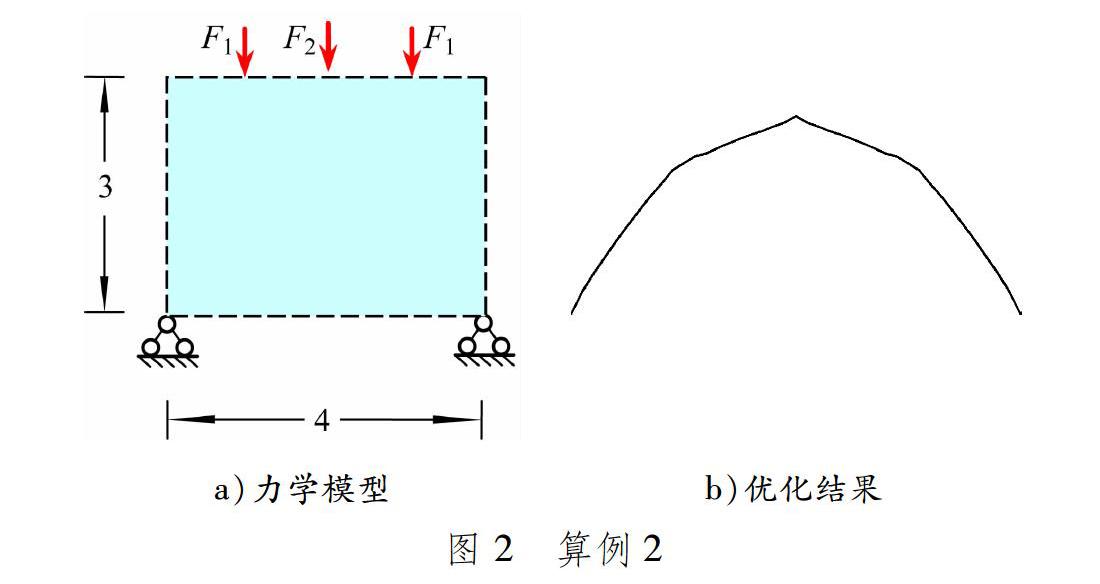
算例2选择在结构跨中和左右1/4跨分别不同时作用F1和F2，F1=F2/2，其力学模型见图2a）。杆件竖向密度质心连线表示的拓扑优化结果见图2b）。

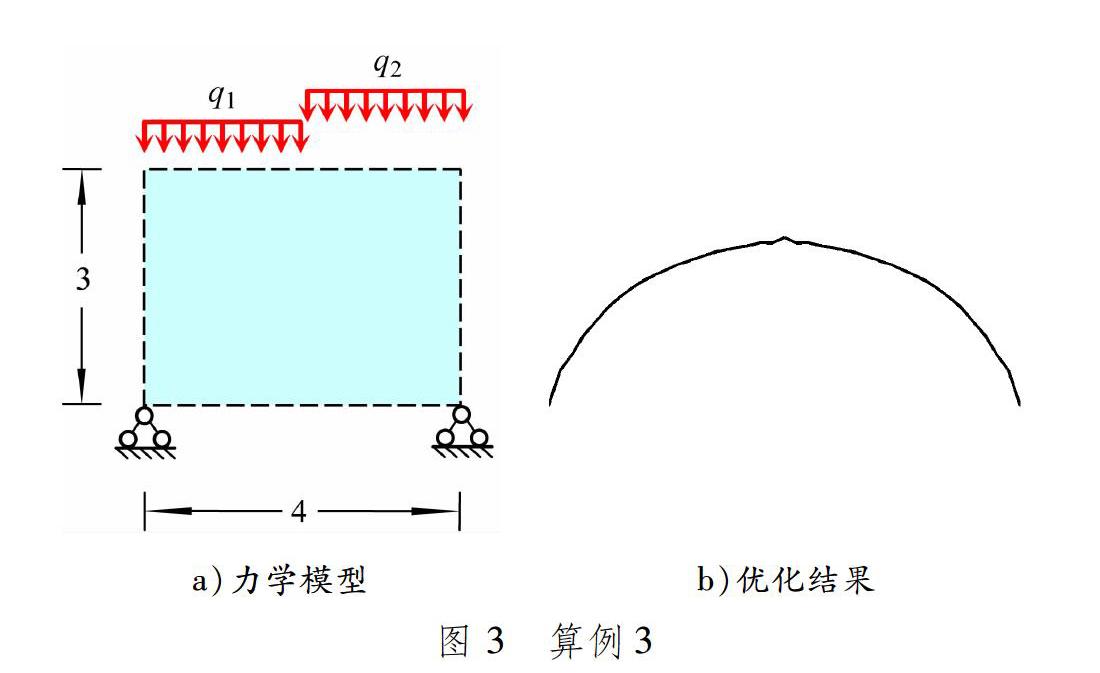
算例3为在结构左、右半跨分别不同时作用均布载荷q1和q2，q1=q2，其力学模型见图3a）。拓扑优化结果见图3b）。

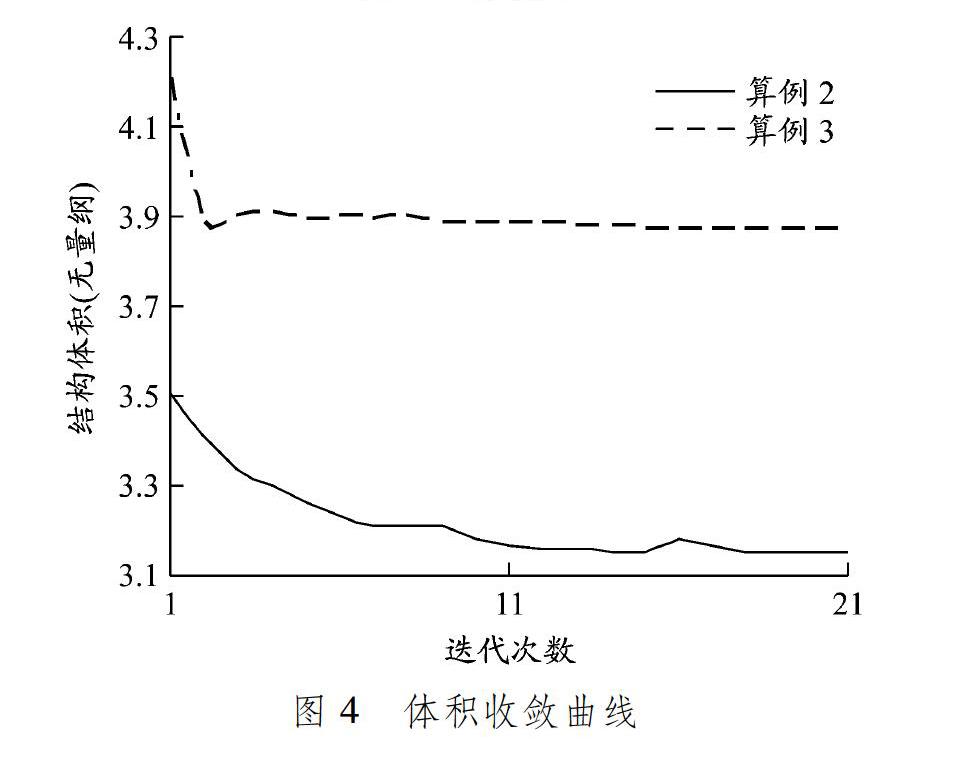
算例2和算例3的体积收敛曲线见图4，可知程序收敛性良好。

4 結束语

采用类桁架材料模型和有限元方法研究多工况下平面Prager结构的拓扑优化方法。分别计算各单工况下结点的刚度矩阵，通过拟合各单工况下材料的最大方向刚度得出多工况下的刚度矩阵，从而得到拓扑优化结构。算例结果表明该方法可行且有效。在工程实际中，空间壳体结构的载荷条件和边界条件远比上述讨论复杂，复杂拓扑优化问题可考虑将以上方法推广到空间Prager结构的拓扑优化问题，为网壳结构初步设计提供参考。

参考文献：

[1]

沈祖炎， 陈扬骥. 网架与网壳[M]. 上海： 同济大学出版社， 1997： 173-178.

[2]周克民， 李俊峰， 李霞. 结构拓扑优化研究方法综述[J]. 力学进展， 2005， 35（1）： 69-76. DOI： 10.3321/j.issn：1000-0992.2005.01.007.

[3]KEGL M，BRANK B. Shape optimization of truss-stiffened shell structures with variable thickness[J]. Computer Methods in Applied Mechanics and Engineering， 2006， 195（19-22）： 2611-2634. DOI： 10.1016/j.cma.2005.05.020.

[4]DAVID K.Global laminate optimization on geometrically partitioned shell structures[J]. Structural and Multidisciplinary Optimization， 2011， 43（3）：353-368. DOI： 10.1007/s00158-010-0576-9.

[5]ROZVANY G I N，PRAGER W. A new class of structural optimization problem： Optimal archgrids[J]. Computer Methods in Applied Mechanics and Engineering， 1979， 19（1）： 127-150. DOI： 10.1016/0045-7825（79）90038-0.

[6]ROZVANY G I N，NAKAMURA H， KUHNELL B T. Optimal archgrids： Allowance for selfweight[J]. Computer Methods in Applied Mechanics and Engineering， 1980， 24（3）： 287-304. DOI： 10.1016/0045-7825（80）90066-3.

[7]ROZVANY G I N，WANG C M， DOW M. Prager-structures： Archgrids and cable networks of optimal layout[J]. Computer Methods in Applied Mechanics and Engineering， 1982， 31（1）： 91-113. DOI： 10.1016/0045-7825（82）90049- 4.

[8]WANG C M.Optimization of multispan plane Prager-structures with variable support locations[J]. Engineering Structures， 1987， 9（3）： 157-161. DOI： 10.1016/0141-0296（87）90010-1.

[9]ANSOLA R，CANALES J， TRRAGO J A， et al. An integrated approach for shape and topology optimization of shell structures[J]. Computers and Structures， 2002， 80（5/6）： 449- 458. DOI： 10.1016/S0045-7949（02）00019-6.

[10]ZHOU K M，LI X. Topology optimization of structures under multiple load cases using fiber-reinforced composite material

model[J].Computational Mechanics， 2006， 38（2）： 163-170. DOI： 10.1007/s00466-005-0735-9.

[11]ZHOU K M.Optimization of least-weight grillages by finite element method[J]. Structural and Multidisciplinary Optimization， 2009， 38（5）： 525-532. DOI： 10.1007/s00158-008-0305-9.

[12]ZHOU K M，LI X. Topology optimization of truss-like continua with three families of members model under stress constraints[J]. Structural and Multidisciplinary Optimization， 2011， 43（4）： 487- 493. DOI： 10.1007/s00158-010-0584-9.

（编辑 武晓英）