返回舱着陆姿态和动力响应的DEM-FEM耦合分析

梁绍敏 王永滨 季顺迎

摘要：針对返回舱安全着陆问题，采用陆面颗粒离散元模型（discrete element model， DEM）与返回舱壳体有限元模型（finite element method， FEM）相耦合的方法，对返回舱回收着陆过程的动力特性进行数值分析，并与试验结果进行对比，验证计算结果的正确性。分析讨论垂直和倾斜2种着陆姿态的返回舱结构应力分布，从冲击能量的角度讨论陆面颗粒对其缓冲作用。对影响返回舱回弹响应的主要因素进行分析并提出相应的改进方法。结果认为：陆面颗粒是返回舱着陆冲击能量吸收的主体，且倾斜着陆时陆面颗粒吸能占比更加显著;当陆面颗粒之间的摩擦因数较小或返回舱质量较大时，返回舱着陆的回弹速度相对较小。

关键词：返回舱; 着陆姿态; 动力响应; 能量分布; 离散元; 有限元; 模型耦合

中图分类号：V421.32;TB115.1

文献标志码：B

收稿日期：2019-06-21

修回日期：2019-07-14

基金项目： 国家自然科学基金（11572067，11872136）;中央高校基本科研业务费项目（DUT19GJ206）

作者简介： 梁绍敏（1990—），女，河北张家口人，博士研究生，研究方向为颗粒材料缓冲性能，（E-mail）shaominliang@mail.dlut.edu.cn

通信作者： 季顺迎（1972—），男，河北武邑人，教授，博导，博士，研究方向为计算颗粒力学及工程应用，（E-mail）jisy@dlut.edu.cn

DEM-FEM coupling analysis on landing attitude and dynamic response of re-entry capsule

LIANG Shaomin1， WANG Yongbin2， JI Shunying1

（1. State Key Laboratory of Structural Analysis of Industrial Equipment， Dalian University of Technology， Dalian 116024， Liaoning， China; 2. Beijing Institute of Space Mechanics & Electricity， Beijing 100094， China）

Abstract：

As to the safety landing problem of the re-entry capsule， the numerical analysis on the dynamic characteristics of the re-entry capsule during re-entry and landing is carried out using coupling method of land particle discrete element model （DEM） and re-entry capsule finite element model （FEM）. The dynamic characteristics of the re-entry capsule landing are compared with the experimental results， and the correctness of the computational results are verified. The structure stress distribution of the re-entry capsule landing vertical and with oblique postures are discussed， and the buffering effect of surface granules on the re-entry capsule structure is discussed in the terms of impact energy. The main factors affecting the rebound response of the re-entry capsule are analyzed， and the corresponding improvement methods are proposed. The results show that the land surface granules are the main part of the impact energy absorption of the re-entry capsule， and the proportion of energy absorbed by land surface granules is more significant when landing in inclined direction; when the friction factor of land surface granules is smaller and the mass of re-entry capsule is larger， the rebound velocity of the re-entry capsule is relatively smaller.

Key words：

re-entry capsule; landing attitude; dynamic response; energy distribution; discrete element; finite element; model coupling

0 引 言

在航天工程中，探测器太空探测并取样返回是重要的内容之一。探测器返回舱承载大量精密实验仪器和样品，甚至载有宇航员，因此其安全着陆是航天任务成功的重要标志。载人返回舱着陆时的速度一般为6～7 m/s，无人返回舱着陆速度可达10～14 m/s，所以返回舱着陆瞬间会受到较大的冲击力。[1]在不同的着陆速度和舱体姿态下，返回舱中的宇航员受到的冲击载荷会有很大不同。[2]目前，航天飞船主要采用2种方式保证宇航员的安全：（1）水上着落，采用泡沫材料吸收能量，如美国“阿波罗”号飞船的着陆方式;（2）陆地着落，采用机械缓冲结构和材料进行缓冲，如俄罗斯“联盟”号和中国的“神舟”号飞船。[3]返回舱再入大气层时存在“黑障区”，在返回过程中可能偏离预定地点从而使得回收方式及相关缓冲保护装置失效，导致航天员和仪器的安全面临严峻考验。[4]因此，考虑返回舱的着陆姿态对返回任务的成功有重要意义。此外，在着陆过程中，返回舱回弹导致航天任务失败的概率也很大，其中“神舟”五号宇航员在返回着陆过程中唇部受伤就与返回舱的回弹有直接联系。[5]着陆点的特性以及返回舱的着陆姿态不仅是决定返回艙着陆过程运动特性的重要因素，而且对着陆冲击过程中返回舱的回弹产生直接影响，因此，研究返回舱着陆阶段的动力特性对安全着陆分析具有重要的工程意义。

目前，针对返回舱的着陆问题，国内外学者主要采用试验、理论分析和数值模拟等方法进行研究。返回舱水上着落方案的研究以及气囊缓冲系统的研制也为返回舱的安全回收提供一定的保障。[4，6]近年来，随着载人航天事业的迅速发展，我国针对返回舱着陆冲击问题也开展相应的研究。随着计算机技术的提高，数值模拟方法得到空前的发展和应用，其具有计算周期短、计算成本低、重复性好等优点，可为返回舱的相关研究提供先验指导。有限元方法的诞生和广泛应用以及动力学分析软件的不断发展，可为研究返回舱的安全着陆问题提供另一种思路。

然而，针对陆地着陆方式，着陆点由陆面颗粒态物质组成，而颗粒的离散性导致如果采用连续介质模型模拟必然会存在一定的缺陷。离散元方法将颗粒物质看作独立的个体，根据其本身的离散特性构建模型，可有效克服连续介质力学模型的宏观连续假设限制。[7-8]目前，离散元方法已广泛应用于岩土工程[9]、铁路道砟[10-11]以及月壤[12-13]等离散材料的力学性能研究。此外，离散元方法可用于模拟运动过程中颗粒系统的速度场、位移场和力场等的变化[14]，从微观角度解释颗粒的力学特性。由此看来，采用离散元方法对返回舱着陆过程中的陆面颗粒进行数值模拟是可行的。

针对离散介质与连续介质的相互作用，可使用离散元模型（discrete element model， DEM）与有限元模型（finite element method， FEM）耦合方法进行计算分析。自20世纪90年代以来，DEM-FEM耦合方法不断发展和完善，在处理颗粒物质与工程结构和连续介质耦合作用的多尺度问题上有不可替代的优势。该方法可充分发挥有限元和离散元的特点，在解决脆性材料裂纹扩展[15]、局部区域大变形[16]、多尺度界面耦合[17]等问题时具有显著优势。目前，星球车轮与陆壤[18-19]、月壤与着陆器的相互作用[20-21]，以及球磨机、螺旋输送机等方面的应用均可以有效验证DEM-FEM耦合方法的可行性。因此，采用DEM-FEM耦合方法模拟分析返回舱的着陆过程是可行的，研究结果可为返回舱的结构设计和相关试验设计提供理论指导。

本文建立陆面颗粒的DEM和返回舱结构的FEM，通过DEM-FEM耦合方法对返回舱着陆过程进行数值分析，并将计算结果与试验结果进行对比，验证计算方法的可靠性。在此基础上，重点分析在不同着陆姿态下，陆面颗粒对返回舱的缓冲作用以及返回舱动力响应的主要影响因素。

1 返回舱着陆过程的DEM-FEM耦合方法

针对返回舱的着陆过程，采用DEM-FEM耦合方法进行数值分析，建立返回舱的FEM和陆面颗粒的DEM，并通过2个模型之间的参数传递实现耦合，从而模拟陆面颗粒与返回舱之间的相互作用。

1.1 返回舱有限元模型

为减小气流干扰，返回舱被设置为钟罩形侧壁加球冠状大底的密封结构，见图1a）。再入阶段返回舱与空气剧烈摩擦会产生巨大的热量，返回舱外部的隔热结构主要是防止其内部设备的损坏，该部分在着陆过程中不起承重作用，因此在建立模型时可以忽略。[1]返回舱内部的金属结构起主要承重作用，在着陆过程中该结构会发生变形，若压力过大、超过材料的强度，还会导致返回舱着陆失败。本文主要采用平板型壳单元构建内部金属结构，采用共节点的方式连接各单元[22]，建立的返回舱有限元模型见图1b）。

返回舱结构的平板型壳单元示意见图2，其可以看成是平面膜单元和平板弯曲单元的组合[23]。

对于各向同性的壳单元，平面膜单元和平板弯曲单元的变形是相对独立的，为得到收敛于原单元的解，需要精细划分单元。为避免总体刚度矩阵由于单元共面或接近共面而出现奇异性问题，可采用具有附加刚体转角的三角形膜单元GT9和三角形薄板单元TMT组成的广义协调三角形平板型壳单元[12，24]，其单元刚度矩阵可由这2种单元的刚度矩阵组合而成，即

K=kp，11 kp，12 000kp，13 kp，21 kp，22 000kp，23 00kb，11 kb，12 kb，13 000kb，21 kb，22 kb，23 000kb，31 kb，32 kb，33 0kp，31 kp，32 000kp，33

（1）

式中：K为壳单元的刚度矩阵;kp，ij 为平面膜单元的刚度系数;kb，ij 为平板弯曲单元的刚度系数。

1.2 陆面颗粒材料的离散元模型

采用离散元法对陆面颗粒材料的动力过程进行模拟分析。为提高计算效率，采用随机排列球体单元构成陆面颗粒DEM，并通过增加颗粒间的黏结-破碎功能模拟真实非规则颗粒，陆面颗粒的DEM见图3。采用Hertz-Mindlin非线性接触模型计算颗粒间的作用力，主要包括弹性力、黏滞力以及基于Mohr-Coulomb准则的滑动摩擦力。该模型更符合颗粒碰撞的物理过程。[12]黏结单元间的作用力和力矩通过颗粒间的黏结强度传递。[7，10]

返回舱的着陆冲击过程一般历时很短，产生的冲击波只影响有限的陆面面积。为提高计算效率，可以建立有限的陆面域，对其下边界和四周边界采用无反射边界条件，模拟无限空间陆面域。冲击波在陆面中传播距离的计算方法[25]为

式中：D为返回舱撞击地面时冲击波在陆面中的传播距离，m;α为由陆面颗粒材料决定的因数，其取值范围一般为0.42～0.80[1];M为返回舱的质量，t;H为返回舱等效自由下落高度，可根据着陆速度计算，m。为满足陆面计算域且保证计算效率，设置的颗粒粒径大于实际陆面颗粒的粒径，通过增加颗粒间的阻尼和黏结强度消除由此产生的误差。

1.3 返回舱着陆过程DEM-FEM耦合方法

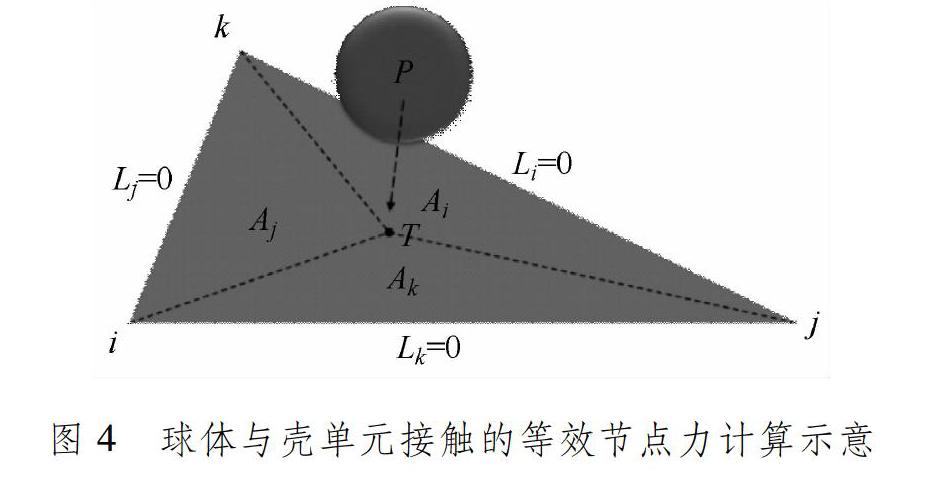
基于陆面颗粒的DEM和返回舱的FEM，采用DEM-FEM耦合法分析陆面颗粒与返回舱结构相互作用的过程时，两个模型间的参数传递尤为重要。[17，26]在有限元计算部分，将颗粒离散单元对返回舱结构壳单元的接触力作为集中载荷，传递到返回舱的FEM，计算返回舱的动力响应并更新结构位移;将更新后的结构位移传递到离散元计算部分，作为离散元的位移边界条件。返回舱结构的位移在节点上计算，因此需要计算接触点的接触力。在着陆过程中，陆面颗粒与返回舱结构的接触位置是随机的，因此需要确定返回舱接触力的等效节点载荷。[27]根据虚功原理可计算球体离散单元与平板型壳单元的等效节点力，即

式中：fDEM 为球体离散单元与壳单元的接触力;

Pe，f 为等效节点力;

N为单元的形函数。采用面积坐标作为三角形单元的形函数，球体与壳单元接触的等效节点力计算示意见图4。

三角形面积坐标可由接触点坐标计算，即

Ni=Li=Ai/A （4）

式中：Li为三角形的面积坐标分量;Ai为离散单元与三角面的作用点和另外2个单元节点围成的面积;A为三角形单元的整体面积。

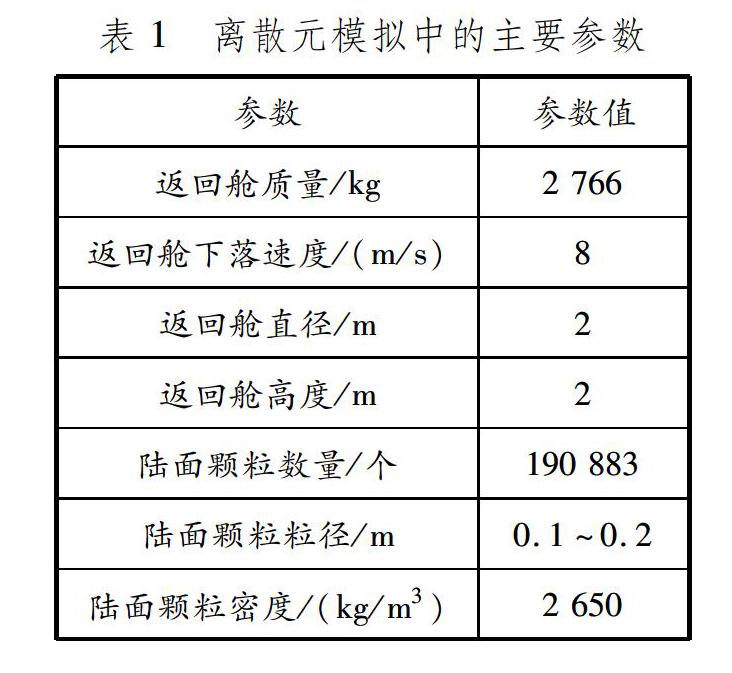
在DEM-FEM耦合计算过程中，时间步长的选择对计算结果的正确性有重要影响。离散元模拟的时间步长一般为1×10-6s，而有限元模拟的时间步长远小于该值。为提高计算准确率，保证计算信息准确传递，选择离散元模拟的时间步长。为提高计算效率，后续工作将解决不同时间步长下FEM和DEM的参数传递问题。[24]返回舱着陆过程中陆面颗粒离散元模拟的主要计算参数见表1，返回舱与陆面颗粒间的相互作用示意见图5。

2 返回舱着陆过程的DEM-FEM耦合分析

2.1 返回舱着陆过程分析

根据着陆冲击过程的瞬时性，模拟时间选为1.0 s。[28] 在返回舱垂直着陆过程中，陆面颗粒与返回

舱的动力特性见图6。由此可知：在返回舱下落时，其底部中心首先与陆面接触，陆面颗粒因碰撞获得速度后向四周扩散并向上运动，颗粒的运动近似中心对称，返回舱结构与陆面碰撞后有所回弹，发生不明显的倾斜。

取着陆速度为8 m/s，研究返回舱在返回着陆过程中的动力响应，由此获得返回舱所受的冲击载荷和竖向速度曲线，见图7和8。由此可知：最大载荷可达2 600 kN，之后返回舱受到的载荷逐渐减小，最终达到稳定状态;返回舱的速度在与陆面颗粒接触的瞬间迅速减小到0，随后发生回弹获得向上的速度，在0.4 s左右达到稳定状态。速度对时间进行积分可获得位移响应，返回舱竖向位移曲线见图9。由此可知，返回舱在着陆过程中有明显的回弹过程，该回弹特性与返回舱的质量、着陆速度和陆面颗粒材料的力学性质密切相关。

2.2 DEM-FEM模拟结果与力学试验结果对比

为验证DEM-FEM耦合法对返回舱着陆过程数值模拟结果的合理性，选用不同的着陆速度研究返回舱的加速度峰值和最大回弹速度，并与文献[29]中采用LS-DYNA的数值结果和试验结果进行对比，结果见图10。由此可知，采用DEM-FEM耦合方法获得的结果与文献[29]中的试验结果基本吻合，说明本文数值模拟结果正确。随着着陆速度的增大，返回舱结构的加速度峰值呈线性增大，回弹速度也逐渐增加。

2.3 返回舱的着陆姿态分析

根据目前返回舱的着陆速度允许范围，在着陆速度为8 m/s情况下，对比分析返回舱垂直着陆和倾斜着陆2种工况。在倾斜着陆冲击过程中，6个不同时刻返回舱的姿态变化见图11。由此可知，当返回舱的大底边缘与陆面接触后，返回舱结构逐渐变为垂直状态，随后向相反方向倾斜，但倾斜角度較小。与垂直着陆工况相比，倾斜着陆时产生的撞击坑较深。

在不同着陆速度下，2种着陆姿态返回舱的动态响应对比见图12。由此可知：垂直着陆的加速度峰值、回弹速度和冲击力峰值均大于倾斜着陆，倾斜着陆的撞击坑深度大于垂直着陆，说明倾斜着陆更有利于安全着陆。

在2种着陆姿态下，不同时刻返回舱结构的VON Mises应力云图见图13。对比分析发现：倾斜着陆时最大应力出现较早，且高应力分布区域较大;垂直着陆时的最大应力大于倾斜着陆时的最大应力;垂直着陆时的应力近似对称分布，倾斜着陆时的较大应力主要集中在大底中心和着陆点附近，这表明着陆时的主要承力区域为接触点。

以着陆速度8 m/s的情况为例，当返回舱的结构应力达到最大值时，根据返回舱着陆冲击前、后结构能量变化情况，可统计结构的动能和陆面表面颗粒的动能，由此得出着陆冲击能量的分配情况，见表2。由此可知，陆面是返回舱着陆冲击能量吸收的主体，吸收能量的占比达到50%左右。由图13可知，返回舱的大底在冲击过程中承受主要的冲击力。与垂直着陆相比，倾斜着陆时返回舱结构吸能比例明显减小，但倾斜着陆时陆地表面颗粒吸收能量占比增加。因此，倾斜着陆更有利于吸收返回舱的机械能。

陆面表面的颗粒性物质存在缓冲耗能的特性。在外部载荷作用下，颗粒间发生强烈的挤压和摩擦，其内部复杂的力链结构发生断裂和重组，从而消耗

大量的能量。[30]颗粒间存在黏滞作用和塑性变形，可吸收不可逆转的能量。在颗粒系统中，接触力通过力链传递，使得局部冲击载荷在空间上不断扩展，进而降低冲击强度。此外，力链在力的传播过程中具有显著的时间效应，将瞬时冲击载荷在时间上进行延迟，这在一定程度上起缓冲作用。[30]着陆冲击过程中陆面颗粒截面的速度分布见图14a）。由此可知，颗粒的速度接近对称分布，存在明显的三角区域，与返回舱距离较近的颗粒速度较大并向四周发散，可直观体现颗粒之间动量的传递。着陆冲击过程中陆面颗粒间的力链结构见图14b），可反映颗粒之間的相互作用以及力的传递过程。由此可知：冲击作用力由接触点向四周发散传递，较大的作用力主要集中在返回舱结构的正下方。

2.4 返回舱的回弹响应分析

返回舱在着陆过程中的回弹对试验设备甚至宇航员都会造成严重影响，因此有必要研究影响返回舱回弹的原因，并提出避免回弹的方案。前文分析发现，倾斜着陆比垂直着陆的回弹速度小，这主要是因为倾斜着陆时返回舱结构与陆面接触的时间长，有利于结构与颗粒之间能量的传递。此外，回弹速度随着陆速度的增大而增大，且呈现线性关系。在实际着陆过程中，可改变的因素主要是返回舱的结构和着陆点的选择。

由于颗粒间的摩擦因数直接影响颗粒之间的相互作用，尤其是颗粒间的动量传递和能量传递。不同摩擦因数下返回舱的回弹速度见图15。由此可知，随着颗粒间摩擦因数的增大，返回舱的回弹速度线性增大。在理想情况下，当颗粒间的摩擦因数足够小时，返回舱的回弹速度可以接近0。这说明当着陆点颗粒的光滑度达到一定值时，可以保证返回舱不发生回弹。因此，为防止返回舱的回弹，有必要建立人工回收场地，铺洒特殊的人造颗粒，尽量减小摩擦因数。

返回舱的自身质量也是影响其回弹的因素之一，所以对制造返回舱的材料要求很高，同时对航天器搭载的实验设备的质量也有一定要求。不同质量的返回舱着陆过程中回弹速度的变化见图16。由此可知，随着返回舱质量的增大，回弹速度减小，当质量达到4 700 kg时，返回舱将不再回弹，这主要是惯性的原因。应结合返回舱内部空间等方面的要求，综合考虑返回舱的质量设计，选择合适的质量域，协调满足各方面的要求。

以上分析发现，当陆面颗粒之间的摩擦因数较小、返回舱质量较大时，返回舱的回弹速度较小。因此，返回舱的回收着陆点选择需要尽量满足以上条件，以保障返回舱的安全着陆。

3 结 论

基于DEM-FEM耦合法对返回舱的回收着陆动力过程进行数值模拟。

分析返回舱着陆时的动力学特性和相应的时程曲线，发现返回舱受到的载荷存在较大的峰值，且在着陆过程中有明显回弹。

结构的最大加速度和回弹速度与试验结果对比发现，采用DEM-FEM耦合法的计算结果与试验结果基本一致，证明该方法合理。

对比分析垂直和倾斜2种着陆姿态下返回舱的动力响应，发现倾斜着陆时撞击坑较深且结构与颗粒的作用时间较长。对比2种着陆姿态下结构的应力云图，发现着陆时的主要承力区域为接触点附近，倾斜着陆过程中的最大应力比垂直着陆过程中的小。

从能量耗散角度分析陆面颗粒对返回舱的缓冲作用，发现陆面颗粒是返回舱着陆冲击能量吸收的主体，倾斜着陆时陆面颗粒吸能占比明显比垂直着陆时的大。这主要是由于离散颗粒之间可以形成力链，其断裂和重组可耗散系统的机械能;倾斜着陆有利于返回舱与颗粒的接触，延长作用时间，有利于系统能量的耗散。

分析返回舱回弹响应，发现当陆面颗粒之间的摩擦因数较小、返回舱质量较大时返回舱的回弹速度较小。

参考文献：

[1]张大鹏， 雷勇军. 深空探测返回舱着陆冲击动力学分析[J]. 深空探测学报， 2014， 1（2）： 150-155. DOI： 10.15982/j.issn.2095-7777.2014.02.011.

[2]马春生， 黄世霖， 张金换， 等. LS-DYNA的ALE方法在飞船返回舱着落仿真中的应用[J]. 清华大学学报（自然科学版）， 2006，46（8）： 1455-1457.

[3]杜汇良， 黄世霖， 张金换. 航天飞船座椅着陆缓冲系统的力学模型[J]. 清华大学学报（自然科学版）， 2004， 44（5）： 717-720.

[4]王宇翔， 杜汇良， 马春生， 等. 飞船返回舱着水与着陆工况冲击兼容性设计分析[J]. 振动与冲击， 2012， 31（9）： 94-97.

[5]易中贵， 戈新生. 自由下落猫姿态最优控制的混合优化策略[J]. 力学学报， 2016， 48（6）： 1390-1397. DOI： 10.6052/0459-1879-16-189.

[6]房红军， 杨雷. 返回舱着水冲击过载近似模型建模与分析[J]. 航天器工程， 2018， 27（3）： 39- 44. DOI： 10.3969/j.issn.1673-8748.2018.03.006.

[7]梁绍敏， 王永滨， 季顺迎. 基于离散元方法的月球着陆器冲击月壤过程分析[J]. 航天返回与遥感， 2017， 38（4）： 55-63. DOI： 10.3969/j.issn.1009-8518.2017.04.007.

[8]TAVAREZF A， PLESHA M E. Discrete element method for modelling solid and particulate materials[J]. International Journal for Numerical Methods in Engineering， 2007， 70（4）： 379- 404. DOI： 10.1002/nme.1881.

[9]SITHARAMT G， VINOD J S. Evaluation of shear modulus and damping ratio of granular materials using discrete element approach[J]. Geotechnical and Geological Engineering， 2010， 28（5）： 591-601. DOI： 10.1007/s10706-010-9317-5.

[10]季顺迎， 赵金凤， 狄少丞， 等. 面向环境力学的离散元分析软件研发和工程应用[J]. 计算机辅助工程， 2014， 23（1）： 69-75. DOI： 10.13340/j.cae.2014.01.014.

[11]LOBO-GUERREROS， VALLEJO L E. Discrete element method analysis of railtrack ballast degradation during cyclic loading[J]. Granular Matter， 2006， 8（3）： 195-204. DOI： 10.1007/s10035-006-0006-2.

[12]梁绍敏， 王永滨， 王立武， 等. 月球着陆器着陆过程的DEM-FEM耦合分析[J]. 固体力学学报， 2019， 40（1）： 39-50. DOI： 10.19636/j.cnki.cjsm42-1250/o3.2018.041.

[13]林呈祥， 凌道盛， 钟世英. 模拟月壤抗剪强度试验研究及离散元分析[J]. 岩土力学， 2017， 38（3）： 893-901. DOI： 10.16285/j.rsm.2017.03.035.

[14]LIY J， DOVE A， CURTIS J S， et al. 3D DEM simulations and experiments exploring low-velocity projectile impacts into a granular bed[J]. Powder Technology， 2016（288）： 303-314. DOI： 10.1016/j.powtec.2015.11.022.

[15]HADDADH， GUESSASMA M， FORTIN J. A DEM-FEM coupling based approach simulating thermomechanical behaviour of frictional bodies with interface layer[J]. International Journal of Solids and Structures， 2016（81）： 203-218. DOI： 10.1016/j.ijsolstr.2015.11.026.

[16]XUW， ZANG M Y. Four-point combined DE/FE algorithm for brittle fracture analysis of laminated glass[J]. International Journal of Solids and Structures， 2014， 51（10）： 1890-1900. DOI： 10.1016/j.ijsolstr.2014.01.026.

[17]徐伟， 臧孟炎. DEM与FEM动态耦合算法研究[J]. 计算力学学报， 2013， 30（5）： 671-676. DOI： 10.7511/jslx201305013.

[18]NAKASHIMAH， FUJII H， OIDA A， et al. Parametric analysis of lugged wheel performance for a lunar microrover by means of DEM[J]. Journal of Terramechanics， 2007， 44（2）： 153-162. DOI： 10.1016/j.jterra.2005.11.001.

[19]BHUVARAGHANB， SRINIVASAN S M， MAFFEO B， et al. Shot peening simulation using discrete and finite element methods[J]. Advances in Engineering Software， 2010， 41（12）： 1266-1276. DOI： 10.1016/j.advengsoft.2010.09.003.

[20]蒋万松， 黄伟， 沈祖炜， 等. 月球探测器软着陆动力学仿真[J]. 宇航学报， 2011， 32（3）： 462- 469. DOI： 10.3873/j.issn.1000-1328.2011.03.002.

[21]朱汪， 杨建中. 月球着陆器软着陆机构着陆稳定性仿真分析[J]. 宇航学报， 2009， 30（5）： 1792-1796. DOI： 10.3873/j.issn.1000-1328.2009.05.008.

[22]李治宇， 杨彦广， 袁先旭， 等. 返回舱模型参数化方法研究[J]. 计算机仿真， 2013， 30（1）： 104-109. DOI： 10.3969/j.issn.1006-9348.2013.01.025.

[23]LONGY Q， XU Y. Generalized conforming quadrilateral membrane element with vertex rigid rotational freedom[J]. Computers & Structures， 1994， 52（4）： 749-755. DOI： 10.1016/0045-7949（94）90356-5.

[24]PARKJ W， SONG J J. Numerical simulation of direct shear test on rock joint using bonded-particle model[J]. International Journal of Rock Mechanicsand Mining Sciences， 2009， 46（8）： 1315-1328. DOI： 10.1016/j.ijrmms.2009.03.007.

[25]孔令伟， 袁建新. 强夯的边界接触应力与沉降特性研究[J]. 岩土工程学报， 1998（2）： 86-92.

[26]郑敏， 蒋明镜， 申志福. 简化接触模型的月壤离散元数值分析[J]. 岩土力学， 2011， 32（S1）： 766-771. DOI： 10.16285/j.rsm.2011.s1.002.

[27]NITKAM， COMBE G， DASCALU C， et al. Two-scale modeling of granular materials： A DEM-FEM approach[J]. Granular Matter， 2011， 13（3）： 277-281.DOI： 10.1007/s10035-011-0255-6.

[28]张大鹏， 雷勇军. 返回舱着陆冲击过程的仿真分析[J]. 固體力学学报， 2013， 33（S1）： 14-19. DOI： 10.19636/j.cnki.cjsm42-1250/o3.2013.s1.003.

[29]杜汇良. 飞船返回舱故障着陆冲击缓冲系统改进设计计算分析[D]. 北京： 清华大学， 2003.

[30]季顺迎， 李鹏飞， 陈晓东. 冲击荷载下颗粒物质缓冲性能的试验研究[J]. 物理学报， 2012， 61（18）： 301-307.

（编辑 武晓英）