随机振动和谐波载荷下基于相对位移分析的结构间隙变化评估

摘要：为正确评估紧凑结构在外载荷作用下的安全性，推导随机振动和谐波载荷下相对位移的理论计算方法，考虑响应点之间相关性，并以某工程结构有限元分析为例，对随机振动和谐波载荷下结构中的间隙变化进行评估。将谐波载荷与随机振动载荷进行等效转换，数值模拟结果表明2种方法的计算结果完全吻合，相互验证分析方法的有效性和正确性。

关键词：随机振动; 谐响应; 相对位移; 相关性; 数值模拟; 有限元

中图分类号：O327; TB115.1

文献标志码：A

Structure gap change evaluation under random vibration and

harmonic excitation based on analysis of relative displacement

HU Jie

（Institute of System Engineering， China Academy of Engineering Physics， Mianyang 621999， Sichuan， China;

Shock and Vibration of Engineering Materials and Structures Key Laboratory of Sichuan Province，

Mianyang 621999， Sichuan， China）

Abstract：

To correctly evaluate the safety of compact structures under external excitation， the relative displacement calculation method is theoretically deduced under random vibration and harmonic excitation. The correlation between response points is considered， and the change of gap in structure under random vibration and harmonic excitation is evaluated by taking the finite element analysis of an engineering structure as an example. The equivalent conversion between harmonic excitation and random vibration excitation are done. The numerical simulation results show that the two methods are agree well with each other， which can prove the effectiveness and correctness of two analytical methods.

Key words：

random vibration; harmonic response; relative displacement; correlation; numerical simulation; finite element

收稿日期：2019-06-01

修回日期：2019-07-09

作者簡介：

胡杰（1982—），男，湖南岳阳人，副研究员，博士，研究方向为结构动力学，（E-mail）401hujie@caep.cn

0 引 言

相对位移可评估外载荷作用下结构之间发生碰撞的可能性。在设计方案阶段开展数值仿真，可尽量降低设计失当风险，在工程领域中应用广泛。

在结构设计中，由于空间限制或者其他结构紧凑性要求，结构中往往存在许多小的间隙。在外载荷作用下，组件之间可能发生碰撞。冯玉龙等[1]采用有限元法计算增压载荷下飞机舱门与对应机头结构的相对位移。在建筑抗震分析领域，主要考虑地震载荷下相邻建筑结构之间是否会发生碰撞。FAGHIHMALEKI等[2]针对近场和远场地震，通过数值模拟分析建筑结构之间的最大相对位移。国巍等[3]针对铁路客运站建筑与桥梁结构在地震载荷下可能发生碰撞的隐患，开展动力学时程数值模拟，指出目前还缺乏对房屋与桥梁结构间安全距离统一的设计指导规范。白凤龙等[4]研究桥梁相邻结构在地震载荷下的碰撞问题，指出抗震设计标准中推荐的调整相邻结构基本频率相近、减小相邻结构间的相对位移的建议仅在地震动空间变化效应可以忽略的前提下有效。此外，LI等[5-6]和LU等[7]通过传感器实时监测，基于测试数据分析研究不同类型建筑结构的相对位移。在医学领域，何黎明等[8]和李海岩等[9]基于有限元法，在关注区域设置弹簧单元，进行冲击载荷下颅骨-脑相对位移的数值模拟。李海岩等[10]又构建生物仿真度更高的第95百分位中国人头部有限元模型，获得与试验结果基本吻合的颅骨-脑相对位移曲线，为交通事故中头部损伤机理的研究提供理论依据。

上述研究涉及的外载荷大体可分为2类：一类是静载荷，如增压载荷，此时结构的位移变形基本恒定，在评估相对位移时可直接将变形结果进行简单的几何加减;另一类是动载荷，如地震载荷和冲击载荷，与时间历程相关，分析时间都较短，可以通过关注位置之间的响应时间历程对比分析相对位移。对于随机振动载荷，由于其具有宽频率、长时间等特点，结构的响应是随机的，结构上各点之间的响应存在相关性，各点之间的相对位移也具有随机特性，这使得评估振动载荷作用下结构之间的相对位移更复杂，对此鲜有文献涉及。

本文针对随机振动和谐波2种振动载荷，推导相对位移计算公式，考虑响应之间的相关性，进行典型工程结构有限元数值模拟，并通过载荷等效转换，相互验证计算公式的有效性。

1 随机振动载荷下的结构相对位移 计算方法

记A和B为结构上关注的2个点，在随机振动载荷作用下，其响应是随机变量，假定该变量满足正态分布。记A、B点在随机振动载荷下x方向的位移响应分别为UAx 和UBx ，根据统计分析方法，A、B两点之间在x方向的相对变形D（Ux）的计算公式为

D（Ux）=D（UAx -UBx ）=

D（UAx ）+D（UBx ）-2C（UAx -UBx ）

（1）

式中：D（UAx ）和D（UBx ）分别为A、B两点在x方向的位移响应方差;C（UAx -UBx ）为A、B两点在x方向的位移响应协方差。

同理，A、B兩点之间在y方向和z方向的相对变形D（Uy）和D（Uz）的计算公式分别为

D（Uy）=D（UAy -UBy ）=

D（UAy ）+D（UBy ）-2C（UAy -UBy ）

（2）

D（Uz）=D（UAz -UBz ）=

D（UAz ）+D（UBz ）-2C（UAz -UBz ）

（3）

上述公式考虑两个随机变量之间的相关性。根据工程分析需要，随机振动分析的计算结果需取3倍均方根值，以满足99.73%的置信度。

2 谐波载荷下的结构相对位移计算方法

在谐波载荷下，结构响应为谱形式，可用复数形式表示。记结构上A、B两点的位移响应谱分别为

RA=RAr （ω）+iRAi （ω）

RB=RBr （ω）+iRBi （ω）

（4）

其中虚部包含响应的相位信息，将这2点的响应相减，可得到A、B两点相对位移RAB 的复数形式为

RAB =RA-RB=

RAr （ω）-RBr （ω）+i（RAi （ω）-RBi （ω））

（5）

RAB 中的虚部反映A、B两点的相位差，也体现两点响应之间的相关性。

3 随机振动载荷与谐波载荷的等效换算

在随机振动载荷下，结构响应的分析结果不包含相位信息，其相关性通过协方差体现，相对位移以均方根形式表现。在谐波载荷下，结构响应可通过复数形式（或以幅值结合相位的形式）体现，其虚部包含相位信息，相对位移可以用响应谱的差表示，并以复数形式的谱表征，该复数谱的幅值就可用来衡量相对位移的大小。

实际上，若将随机振动载荷与谐波载荷进行等效换算，这2种载荷作用下得到的结构相对位移结果应当吻合。随机振动载荷与谐波载荷的量纲不同，两者之间的换算关系为

P（ω）=Q2（ω）/df

（6）

式中：P（ω）为随机振动载荷的功率谱密度;Q（ω）为谐波载荷的幅值谱;df为频率分辨率。

4 数值模拟

4.1 结构模型

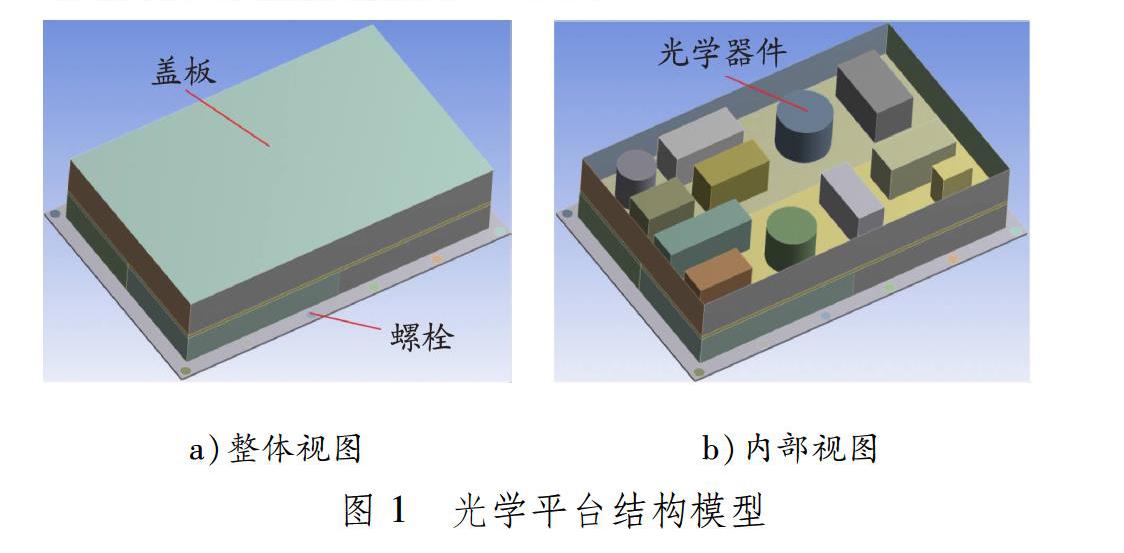
某光学平台结构模型见图1。该平台底部通过12个螺栓安装于其他结构上，诸多光学器件安装于同一平面，上覆盖板，光学器件高度相同，盖板与光学器件之间的间隙为5 mm。

4.2 随机振动载荷下的相对位移数值模拟

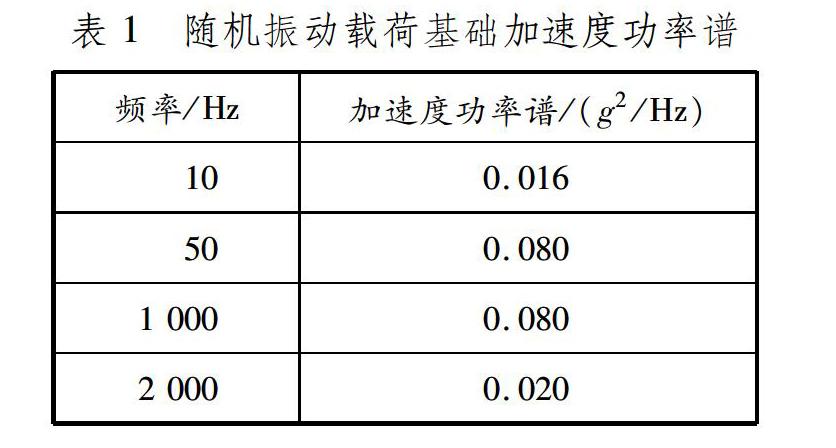
随机振动载荷基础加速度功率谱见表1。载荷方向为横向，分析在该随机振动载荷下，盖板是否会与光学器件发生碰撞。

采用Workbench进行建模和计算，结构节点位移响应的均方根值可以直接获得，但两节点响应之间的协方差无法直接获取。在算例中，将计算结果在ANSYS经典界面打开，采用APDL后处理得到协方差，然后通过式（1）～（3）进行计算。

得到的光学器件横向位移响应均方根分布见图2。若盖板与光学器件发生碰撞，则碰撞位置应在光学器件上表面的边缘，因此选择光学器件上表面横向位移响应最大的A点作为评估对象，并取盖板下表面与A点正对应的点作为B点。

由式（1）计算得到随机振动载荷下A、B两点之间位移的3倍均方根值为4.086 mm，小于盖板与光学器件之间的间隙（5 mm），因此不会发生碰撞。

4.3 谐波载荷下的相对位移数值模拟

假设频率分辨率df=0.5 Hz，根据式（6）将表1中的随机振动载荷换算为谐波载荷，见图3。计算得到A、B两点相对位移的幅值谱和相位差谱，见图4。

幅值谱的3倍均方根值为4.085 mm，与随机振动载荷下的结果吻合，说明这2种计算相对位移的方法有效，相互验证准确性。需要说明的是，验证结果与频率分辨率取值无关，因为随机振动载荷向谐波载荷转换的位移，与谐波载荷转换为随机振动响应的幅值相互抵消。

5 结束语

动载荷下的结构间隙变化评估，可通过对相对位移的分析计算进行研究，且必须要考虑响应点之间的相关性。在随机振动载荷下，相关性通过协方差表征;在谐波载荷下，相关性通过相位差表征，给出随机振动和谐波载荷下的相对位移计算公式。同时，在频率分辨率已知的情况下，谐波载荷与随机载荷可以等效转换，2种载荷形式下的相对位移数值计算结果高度吻合，相互验证分析方法的准确性和有效性。

参考文献：

[1]冯玉龙， 方雄. 飞机舱门结构相对位移的分析方法[J]. 应用数学和力学， 2014， 35（S1）： 95-98.

[2]FAGHIHMALEKIH， AHMADIAN F， ROOSTA H. Effect of far field and near field earthquakes on hysteresis energy and relative displacement of steel moment resisting frame structures[J]. Journal of Building Pathology and Rehabilitation， 2017， 2（5）： 1-9. DOI： 10.1007/s41024-017-0024-y.

[3]国巍， 余志武. 一种计算地震作用下相邻结构相对位移的改进差异谱方法[J]. 土木工程学报， 2012， 45（2）： 68-76. DOI： 10.15951/j.tmgcxb.2012.02.019.

[4]白凤龙， 李宏男. 桥梁相邻结构相对位移反应谱研究[J]. 防灾减灾工程学报， 2013， 33（1）： 62-66. DOI： 10.13409/j.cnki.jdpme.2013.01.011.

[5]LIJ， HAO H. Health monitoring of joint conditions in steel truss bridges with relative displacement sensors[J]. Measurement， 2016（88）： 360-371. DOI： 10.1016/j.measurement.2015.12.009.

[6]LIJ， HAO H. Damage detection of shear connectors under moving loads with relative displacement measurements[J]. Mechanical Systems and Signal Processing， 2015（60/61）： 124-150. DOI： 10.1016/j.ymssp.2014.09.014.

[7]LUM Q， YANG Q S， YANG N. Maximum relative displacement of adjacent buildings during ground motions[J]. Transactions of Tianjin University， 2012， 18（5）： 366-371. DOI： 10.1007/s12209-012-1865-8.

[8]何黎明， 盧亦成， 吴建国， 等. 颅骨-脑相对位移的有限元模拟[J]. 中国微侵袭神经外科杂志， 2005， 10（6）： 263-265. DOI： 10.3969/j.issn.1009-122X.2005.06.009.

[9]李海岩， 李霞， 阮世捷. 颅-脑在头部受直接撞击时相对位移的模拟研究[J]. 中国生物医学工程学报， 2008， 27（3）： 383-388. DOI： 10.3969/j.issn.0258-8021.2008.03.012.

[10]李海岩， 赵玮， 阮世捷， 等. 第95百分位中国人头部颅脑相对位移的有限元评估[J]. 医用生物力学， 2012， 27（2）： 198-206. DOI： 10.16156/j.1004-7220.2012.02.011.