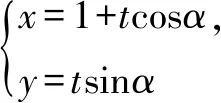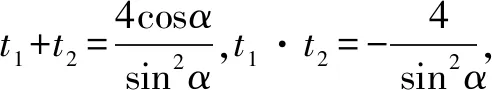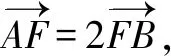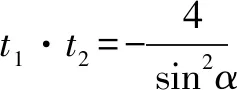2018年浙江卷第17题解法探究

罗文军 刘娟娟

(1.甘肃省秦安县第二中学 741600；2.甘肃省秦安县郭嘉镇槐川初级中学 741600)

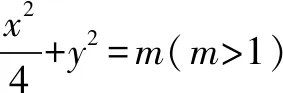
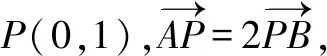
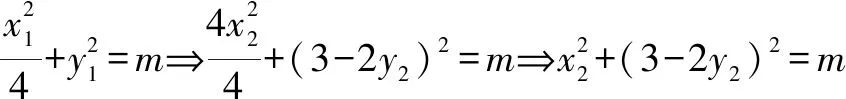
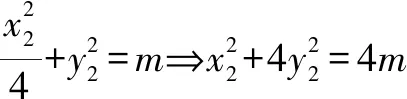
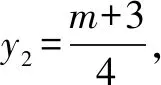
当且仅当m=5时，等号成立.

评注本解法利用向量共线，实现点的坐标之间的转化，结合点在椭圆上，建立方程，应用二次函数的最值解答可得.

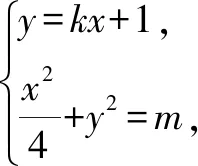
评注本解法利用了斜率参法，将直线方程和椭圆方程联立消元后利用韦达定理，再利用基本不等式求解可得.

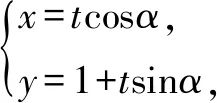
评注本解法利用直线参数方程法，结合参数的几何意义，利用韦达定理，利用基本不等式可求出结果.

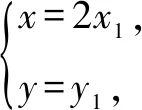
根据伸缩变换的性质，要是点B的横坐标的绝对值越大，等价于点B1的横坐标的绝对值最大，则：

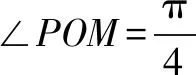
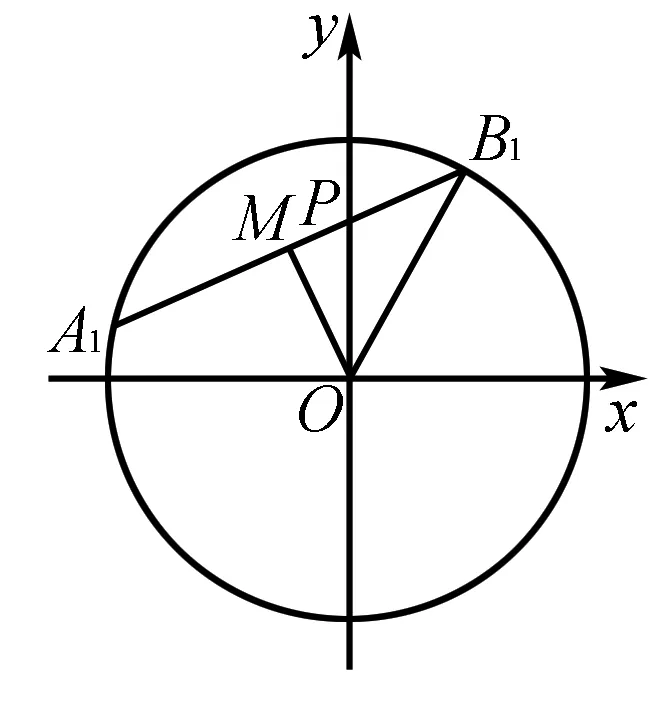
评注本解法利用坐标伸缩变换，将椭圆问题化归为圆的问题，求解可得.

变式1 设抛物线C：y2=4x的焦点F，直线l过F且与C交于A,B两点，若|AF|=2|BF|，求l的方程.

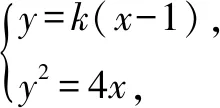
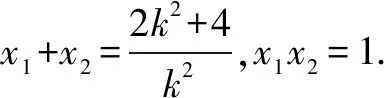
评注本题涉及直线与抛物线的两个交点坐标，没有求出这两个点的坐标，而是设出这两个点的坐标，根据直线方程和抛物线方程联立消元后的方程根的情况，使用根与系数的关系进行整体代入，再结合向量坐标运算求出斜率k的值.这种设而不求的思想是解析几何中处理直线和二次曲线相交问题的最基本方法.

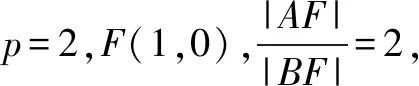
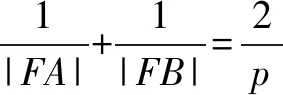
解法3 (定义法)抛物线C:y2=4x的焦点为F(1,0)，准线l′:x=-1，

①设A点在x轴上方、B点在x轴下方时， 过A,B两点分别作抛物线C:y2=4x的准线l′的垂线AA′、BB′,垂足为A′、B′,过B点作BC⊥AA′，且垂足为C,由已知可设|BF|=x，则|AF|=2x.

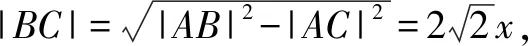
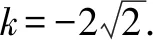
评注本题中，涉及的|AF|和|BF|是抛物线上的点到焦点的距离问题，由抛物线的定义转化为到准线的距离，再结合解直角三角形的知识进行求解.