例谈一题多解的培养与应用

荆 亮

(江苏省徐州市第一中学 221000)

高中数学，融合进众多的数学知识与数学能力，渗透进众多的思维方法与数学素养.本文结合2019年高考真题，就一题多解的培养与应用加以剖析.

一、一题多解有利于培养学生的多种思维能力

一题多解有利于克服传统的定向性、专一性的思维定势，培养学生从多角度、多途径、多层次寻找破解问题的切入点，集中注意力，运用学过的知识等来寻找解题的突破口，有效培养学生的发散性思维能力以及思维的灵活多样性.在解题过程中，通过一题多解，有时还涉及到教材中没有提及的方法，有效开拓解题视野，扩充数学知识，并通过多种解法的对比与分析，进行有效合理比较，总结解题规律，提升解题能力，增强思维品质，进而提升数学核心素养.

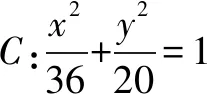
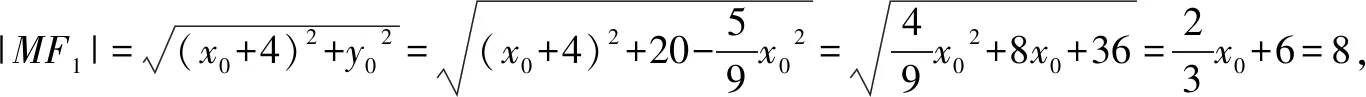
通过圆锥曲线问题的一题多解，结合椭圆的定义、方程与几何性质，直线与椭圆、圆与椭圆的位置关系，两点间的距离公式，等腰三角形的性质等知识点，综合考查运算求解能力，数形结合思想，化归与转化思想，逻辑推理等核心素养，从两点间的距离公式角度、直线的关系关系角度以及圆与椭圆的位置关系角度等切入，有效培养学生对问题的深入理解，形成多种破解方法，提升思维能力.

二、一题多解有利于组合学生的不同知识体系

一题多解有利于克服传统的“一法到底”的单一教学方法，不适合于不同知识层次水平、不同知识体系掌握情况的学生的理解与应用.对于不同学生，由于学生的知识水平层次不同，对相关方法的理解与掌握的程度不同；对于同一学生，由于自身对不同知识体系掌握情况也不尽均衡.因而需要教师在教学过程中关注不同层次的学生，采取不同的方法进行“一题多解”，总有一种方法能比较契合基础不同的学生或更接近学生的知识体系，从而可以听懂、理解与掌握方法，进而有效发现自身不足，合理弥补.

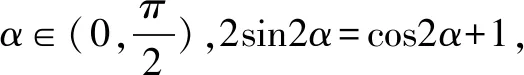
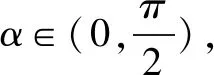
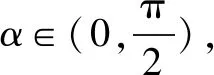
根据不同层次的学生以及同一学生对知识体系的掌握情况，可以从常规角度(平方关系转化法)，能力角度(万能公式法)，原始角度(代入验证法)等不同方法进行“一题多解”.不同的破解方法，总有一种适合，合理与学生的能力进行匹配，选择适合自身能力的方法进行合理思考与破解，为各层面的学生提供破解问题的角度、切入点与方法，从而提升讲解问题的针对性、全面性.

一题多解有利于学生在解决具体问题过程中，根据自己的能力水平与自身情况，寻找较为合适的解题思路，灵活选择有效的问题切入点，寻找破解问题的突破口，从而快速解题，提高效率，提升能力，培养素养.