完全非弹性碰撞损失动能最大的5种证明

谢汝成

(吉林省辽源市第五中学 136200)

碰撞问题是高考的热门考点，其中完全非弹性碰撞更是重中之重，在物体间发生完全非弹性碰过程损失能量最大这一结论上，学生往往知其然而不知其所以然.对学生形成完整的知识脉络造成了障碍.下面笔者将用五种方法来证明这一结论，可以满足不同层次学生对知识的需求，拓宽视野.

一、能量守恒法

例1质量为m1和m2的A和B两个小球用弹簧连接，两者速度分别为v1和v2(其中v1>v2)

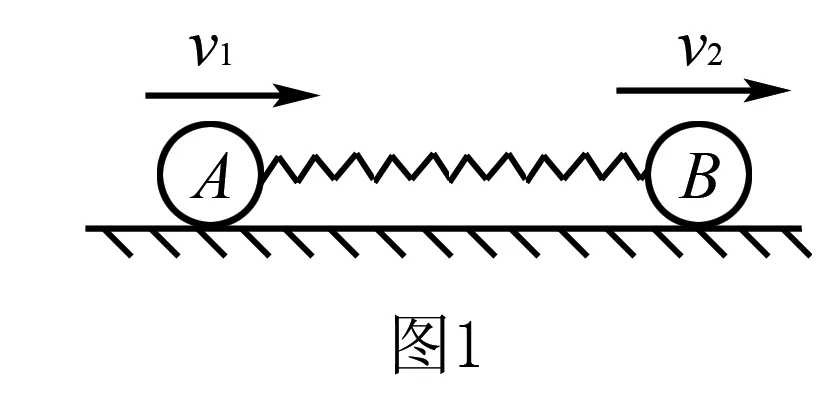
解析系统处于光滑水平面，机械能守恒.系统损失的动能等于弹簧弹性势能增加量.

m1追击m2过程中，当两者共速时，距离最近，弹簧压缩量最大，对应的弹性势能最大，系统损失动能最多，结论得证.

注：(1)在m1和m2距离最近之后，当两者再次共速时，两者距离最远，弹簧伸长量最大，系统损失动能再次达到最多.

(2)若题干中撤去弹簧，A与B直接接触，AB接触部分发生形变，可近似看成弹簧，分析过程与上面解析过程一致.

二、二次函数求极值

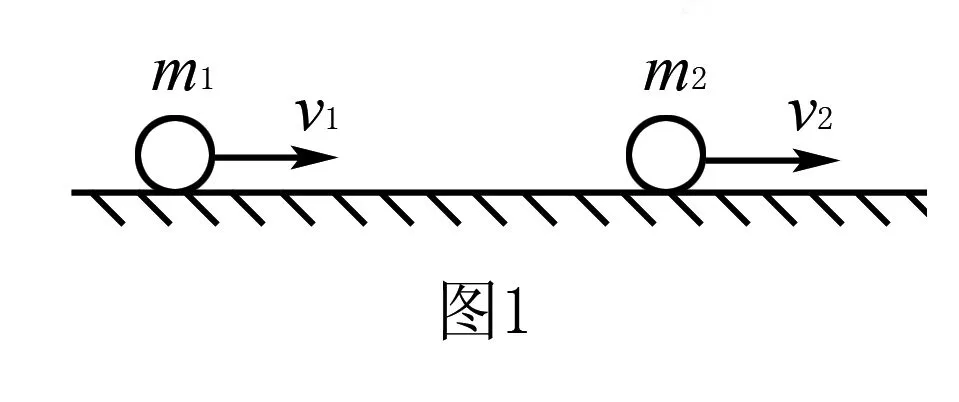
例2如图2所示，光滑水平轨道上一质量为m1，速度为v1的小球A与另一质量为m2，速度为v2的小球B发生正碰,碰后两小球的速度分别为v1′和v2′

解析系统受外力为零，动量守恒

m1v1+m2v2=m1v1′+m2v2′

①

系统损失动能

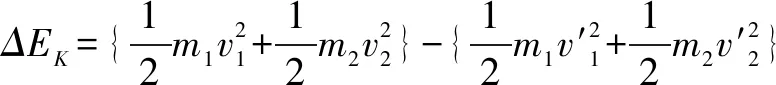
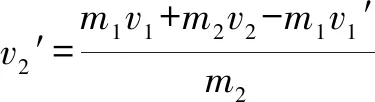
③

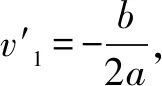
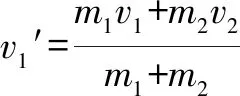
三、求导法

第二种办法在例题2中求解出能量损失ΔEK表达式后利用抛物线的数学特点求解，也可在求出ΔEK的表达式后对ΔEK求导，利用函数特点，导数得零，相应的函数取得极值点，该极值点即为本题求解的最值点.

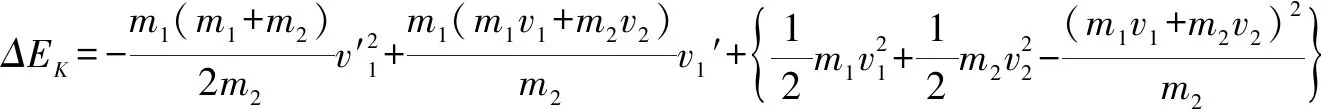
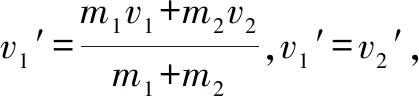
四、质心法

两球体系在固定参考系中的总动能表达式为

以例2为例进行分析：

碰前m1和m2相对质心的靠近速度分别为：(v1-vC)和(vC-v2)，碰后m1和m2相对质心的远离速度分别为(vC-v1′)和(v2′-vC)

两球在光滑水平面运动，系统受外力为零.

即当v1′=v2′=vc时，即碰后两球相对质心动能为零，系统动能损失最多，结论得证.

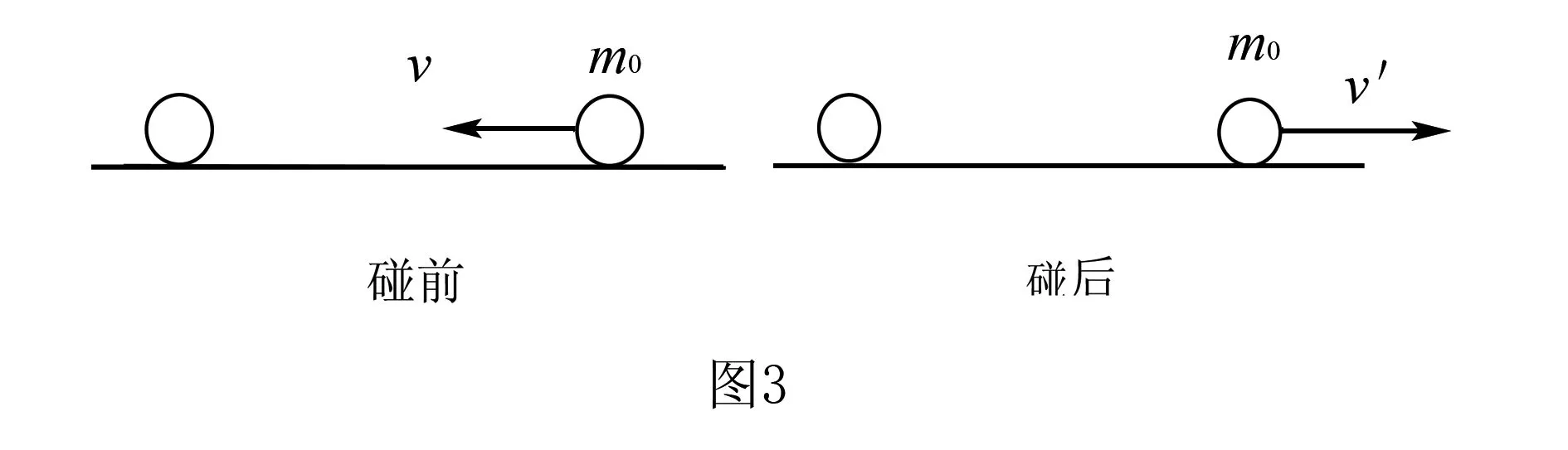
五、折合质量法

以例2为例进行分析