以小见大——例析矢量的应用

黄兴仲

(广东省梅州市丰顺县黄金中学 514357)

在高中物理中，物理量分为标量和矢量.矢量，是指该物理量既有大小，又有方向，其加减运算采用平行四边形法则或多边形法则.高中物理许多物理量均是矢量，深入理解和总结其矢量性，是学习高中物理的重要方法.其看似平凡无奇的知识点，笔者经过梳理，发现内容颇丰，不容小觑.

一、图解法求最值问题

使用图解法求最值问题，主要是利用力的矢量性，当某个物理受到三个力或多个力而平衡时，根据力的矢量性，可将各力头尾相连构成一个封闭的三角形或多边形.若不平衡，可将各力头尾相连，则合力为头指向尾的箭头.

例1一物体质量为m，置于倾角为a的斜面上，如图1所示，物体与斜面间的动摩擦因数为μ，若要使物体沿斜面匀速向上滑动，求拉力的最小值.

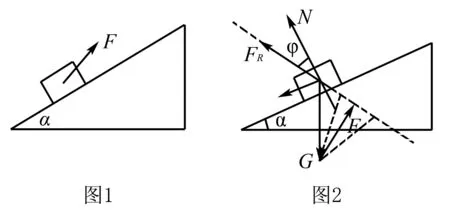
分析此题若采用沿斜面和垂直斜面方向正交分解，设拉力F与斜面所成的夹角为θ，则可得

mgsinα+μ(mgcosα-Fsinθ)=Fcosθ

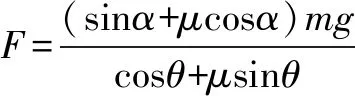
要得出最小值，计算量较大，但此题若采用图解法，则可收到异曲同工的效果.

对该物体分析可知，该物体受到拉力F、重力、动摩擦力和支持力四个力作用，由于动摩擦力与支持力所成的摩擦角φ固定，且其中支持力与动摩擦力的合力为全反力FR，因而可把四力平衡问题转化为三力平衡问题，采用矢量三角形即可，如图2所示.

当F垂直于FR时，此时F最小，为

Fmin=mgsin(φ+α)，

由于tanφ=μ，代入上式，可得

二、转换参考系

在高中研究运动学问题时，有时通过选择恰当的参考系，可为题目带来简便.而转换参考系的基本原理：在位移、速度、加速度等运动学矢量，有着XAB=XAC+XCB，其中X代表物理量，A代表研究对象，角标B、C为对应的参考系，当X代表速度v时，有vAB=vAC+vCB，此即是伽利略速度变换.

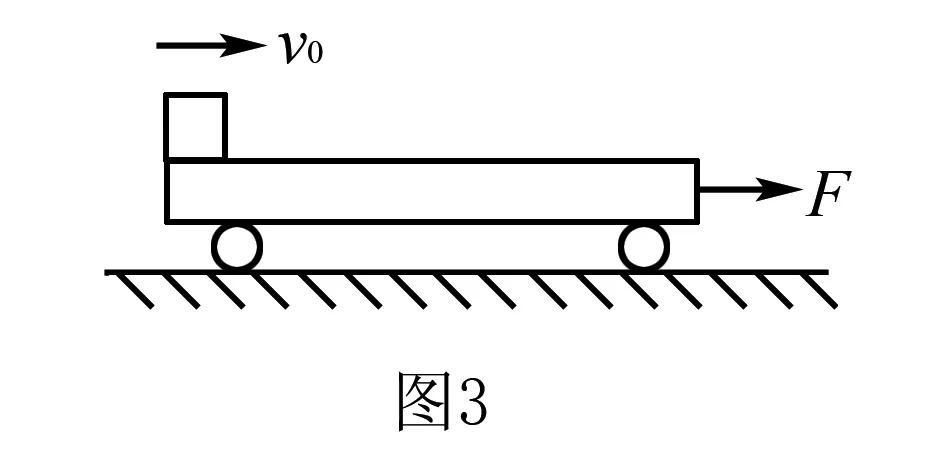
例2如图3所示，平板车静止在光滑水平面上，当小滑块以v0=10m/s的水平初速度从车的左端滑上平板车时，给车施加一个水平向右的恒力F=16N，经过一段时间，小滑块不再相对车滑动.已知平板车质量为M=2kg，滑块质量m=4kg，滑块与平板车之间的动摩擦因数μ=0.4，取g=10m/s2.求滑块相对平板车静止时距车的左端多远？

分析由“小滑块不再相对车滑动”可知，最后小滑块与车保持相对静止，此题要求相对位移，可直接按照在单向运动中，同向时相对位移为两对地位移差的绝对值.也可采用转换参考系，实现快速解题.

解以车为参考系，以v0的方向为正方向，则滑块的初速度为v0′=v0

加速度为a滑车=-a滑地-a车地=-(a滑地+a车地)

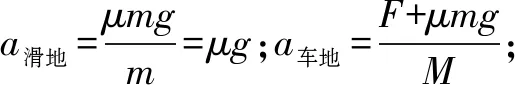
联立以上各式，代入数据得L=2.5 m

点评在高中阶段，转换参考系，可使某些复杂运动转化为简单运动，但该法在使用时也存在一定问题，涉及多过程运动时，往往不采用该种方式，转换过程过于复杂.

三、质点系牛顿第二定律

一个系统含有n个物体，质量分别为m1、m2、m3、……、mn，加速度分别为a1、a2、a3、……、an，系统所受合外力为∑F，则有∑F=ma1+ma2+ma3+…+man，此即为质点系牛顿第二定律.

由质点系牛顿第二定律的矢量性可知，可在某一方向上使用牛顿第二定律，从而为解决加速度不同的连接体问题提供理论基础.

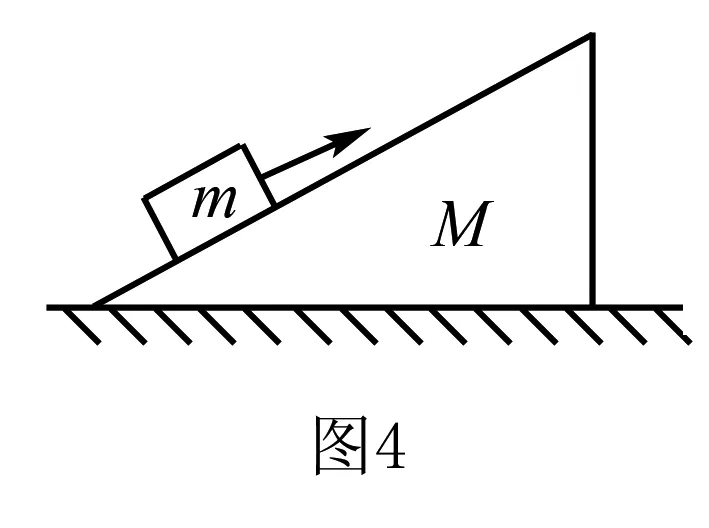
例3如图4所示，质量为M的斜劈形物体放在水平地面上，质量为m的粗糙物块，以某一初速度沿劈的斜面向上滑，至速度为零后又加速返回，而物体M始终保持静止，则在物块m上、下滑块的整个过程中( )

A.地面对物体M的摩擦力方向没有改变

B.地面对物体M的摩擦力方向先向左后向右

C.物块m上、下滑时的加速度大小相同

D.地面对物体M的支持力总小于(M+m)g

分析因物块m与物体M的加速度不同，在高中阶段无法使用整体法进行求解，只可对物块与物体分别进行受力分析，从而推出结论，但该方法过于繁杂.本题可依据质点系牛顿第二定律的矢量性完美解决该类问题.

解假设斜劈形物体与水平面成a夹角，

(1)当物块向上滑动过程中，加速度

将该加速度沿水平方向和竖直方向进行正交分解，对以物块与物体为整体的系统进行受力分析，在水平方向上：f地1=ma1cosα

在竖直方向上：(m+M)g-N1=ma1sinα

结合以上各式，可推出f地1=mgsinαcosα+μmgcos2α，方向水平向左；

N1=(M+m)g-mgsin2α-μmgsinαcosα

(2)当物块向下滑动过程中，加速度

将该加速度沿水平方向和竖直方向进行正交分解，对以物块与物体为整体的系统进行受力分析，在水平方向上：f地2=ma2cosα

在竖直方向上：(m+M)g-N2=ma2sinα

结合以上各式，可推出f地2=mgsinαcosα-μmgcos2α，方向水平向左；

N2=(M+m)g-mgsin2α+μmgsinαcosα

综上所述，可知，AD正确.

四、运动的合成与分解

运动的合成与转换参考系的计算并不一样，运动的合成是指在同一参考系，而转换参考系中的计算是基于参考系的转换.在运动学中位移、速度、加速度均为矢量，因而可将该三个量进行分解，结合运动的合成与分解的等时性、独立性、等效性，从而化普通运动为特殊运动，如常见的平抛运动、斜抛运动、小船渡河等问题.以下以小船渡河为例，说明矢量性在其中的运用.

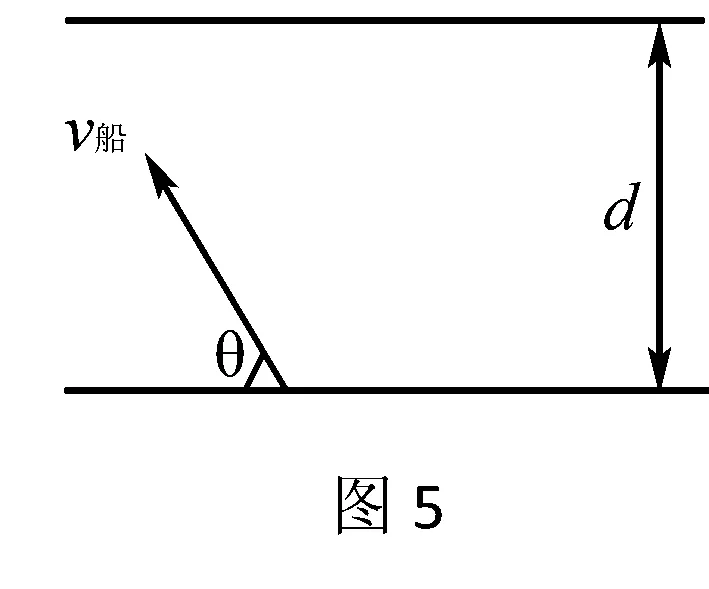
例4设河宽为d，静水中船速为v船，水流速度为v水，船速与河岸的夹角为θ，如图5所示，讨论当θ=?时，船的位移最短？

分析船在水中渡河的位移大小和方向，取决于船速与水速的合速度方向.

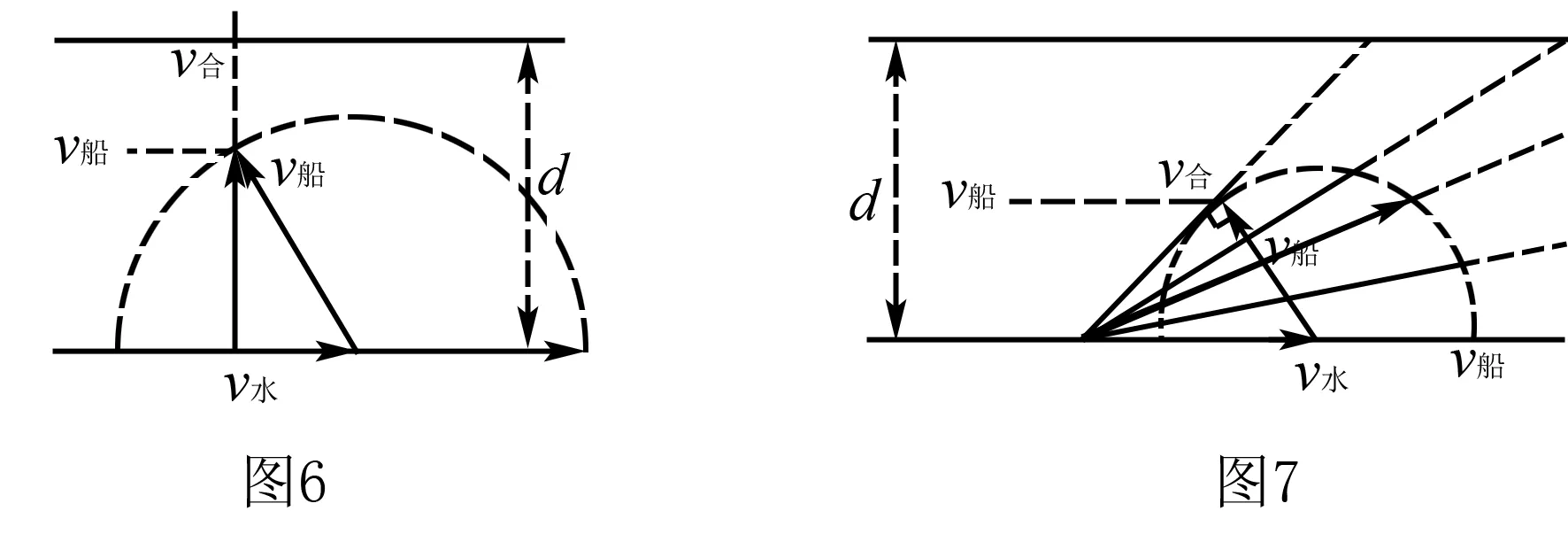
(1)当v船>v水时，如图6，当v合恰好垂直河岸时，合位移最小为d.

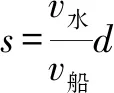
五、公式运用

公式中的运用分别两类，一是依据矢量性，如单方向的动量守恒等，二是矢量的基本运算，主要包括：

(1)矢量与标量的乘除.如E=F/q，由于q是标量，因此当q为正时，E与F同向；当q为负时，E与F反向；

(2)矢量的点乘.如W=F·s，利用矢量的点乘运算，可知W=Fscosa(其中a为F与s的夹角)，功为标量，此即高中阶段做功的定义式W=Fscosα，通过判断力与位移所成的角判断该力做的是正功还是负功.

(3)矢量的叉乘.如f=qv×B，根据叉乘运算，可知洛伦兹力的方向是依据右手螺旋定则进行判断：使右手四指从v跨越小于π的角度转向B，则此时拇指的指向即是f的方向.但由于高中知识受限，因而采用左手定则进行判断.