基本不等式的应用问题例谈
2019-12-19叶珊
叶 珊
(福建省福安市第一中学 355000)
一、求解最值问题
作为函数最值求解的一大重要工具,基本不等式在利用时要注意相应的条件“一正、二定、三相等”.特别在配凑应用时,要注意条件成立的条件,否则容易出现错误.
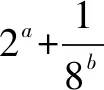

点评利用基本不等式求解代数式的最值问题中,运用时往往需对代数式进行适当地变形(常用的变形技巧是:配方、拆添项、配凑因子和平方等),创造应用基本不等式的条件,要注意应用条件“一正、二定、三相等”.
二、求解参数值问题
在解决一些参数值的求解问题时,经常借助基本不等式来处理,破解的关键是先通过猜测确定参数值,结合基本不等式的应用,利用基本不等式的等号成立时的条件来求解相应的参数值问题.



点评应用基本不等式解决一些问题时,往往要考虑等号成立时所满足的条件,此时也为求解相应的参数值提供条件.特别碰到一些已知相关的方程问题来破解对应参数值问题时,要注意结合关系式的展开,利用基本不等式的应用,再结合相关的不等式、方程等来确定相应的参数值问题.
三、处理恒等式问题
在处理相关的恒等式问题时,关键是进行合理分离参数,把相关原参数的取值范围问题化归为相应函数的最值问题,再利用基本不等式来处理与解决.特别注意:a>f(x)恒成立⟺a>[f(x)]max,a 例3若函数f(x)=32x-(k+1)3x+2,当x∈R时,f(x)>0恒成立,则k的取值范围是( ). 点评将不等式恒成立问题进行合理转化与化归,得以转化为参数恒成立问题,再利用关系式的变形与配凑,借助函数的基本性质与基本不等式来解决相关的函数问题,从而得以确定参数的取值范围.注意在此过程中,经常采用参数分离法来转化. 利用基本不等式确定相应代数式的取值范围问题,关键是巧妙借助基本不等式的变式加以应用,从不同的角度确定相应代数式的最大值与最小值即可. 例4(2018届江苏省扬州中学高三第四次模拟·14)已知x,y均为非负实数,且x+y≤1,则4x2+4y2+(1-x-y)2的取值范围为____. 点评根据基本不等式的有效转化,通过不等式的确定2(x+y)2≤4(x2+y2)≤4(x+y)2,结合参数的引入,分别利用代数式的变换以及二次函数的配方,并结合二次函数的图象与性质来确定相应的最大值与最小值,利用两边夹定理加以综合,从而得以简单快捷破解. 作为基本不等式的一大应用,也经常用来证明一些相关的不等式问题.与综合法相结合,借助所证明不等式的结构特征,利用基本不等式来转化与处理. 点评利用基本不等式来证明对应的不等式时,要注意基本不等式的结构特征,与所要证明的不等式加以合理比较,进行合理的化归与转化.证明时的关键就是对相应的不等式进行必要的变形与转化,再结合基本不等式加以应用. 在解决实际问题中,基本不等式也是用来解决最优化问题的一大工具.实际应用时,要注意基本不等式的条件与实际问题之间的联系与区别. 例6(2017·江苏·10)某公司一年购买某种货物600吨,每次购买x吨,运费为6万元/次,一年的总存储费用为4x万元.要使一年的总运费与总存储费用之和最小,则x的值是____. 点评本题考查实际应用问题,基本不等式,考查应用意识,运算求解能力.此类问题与求解最值问题差不多,只是要根据实际生活问题,往往对参数的取值有一定的限制,如取整点值、取正数值等,要与实际问题相吻合.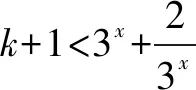
四、确定取值范围问题

五、证明不等式问题


六、解决实际应用问题