低温液体运载火箭变形补偿量设计及试验方法

李 东，冯韶伟，王 月，吴 洁，郑明珠

（1. 北京航空航天大学宇航学院，北京，100191；2. 中国运载火箭技术研究院，北京，100076； 3. 北京宇航系统工程研究所，北京，100076；4. 北京航天计量测试技术研究所，北京，100076）

0 引 言

随着国际空间组织对发射场、落区环境的要求，以液氢-液氧作为推进剂的无毒、无污染的液体运载火箭成为世界各国关注和研发的重点。液氢-液氧是目前液体运载火箭中比冲最高的实用型推进剂组合[1]。然而这种推进剂的温度极低，会在加注、增压过程中造成箭体结构的变形，从而对箭体结构和管路系统设计的补偿量提出更高的要求。

为了计算贮箱在工作过程中的变形量，在工程中通常采用有限元计算方法，该方法能够有效模拟贮箱在增压、加注以及飞行过程中不同载荷条件下箭体结构的变形量，计算结果直观。但有限元方法的计算规模较大造成分析效率较低，难以模拟线膨胀系数随温度的变化规律，且该方法对建模与实物的相符程度要求较高，否则会造成结果失真。

在传统的运载火箭研究过程中，缺少有效的低温加注后变形量系统的试验检测方法，造成试验难以覆盖设计，以及试验结果的外推性不强的难题。

针对运载火箭贮箱的结构特点，本文提出一种低温火箭变形量解析设计方法，获得贮箱在低温、增压作用下的变形量，并基于平面视觉测量原理对试验中的贮箱变形量进行检测，通过与有限元方法及试验结果的对比，验证解析方法的合理性，从而为低温液体运载火箭变形补偿量的设计提供参考和依据。

1 贮箱变形量解析方法

1.1 温度载荷

静定结构在各处均匀的温度载荷作用下，模型各个部件间连接处的位移连续且不会产生应力。由模型的边界条件可认为模型形状将不发生变化，各几何尺寸发生相同比例的伸缩[2]。因此可以认为，在低温液体加注之后，所有区域都由初始温度T0变化到T1，对于长度为l 的贮箱，由温度变化产生的位移δ 为

式中α 为贮箱的材料线膨胀系数，表示温度每变化 1 ℃，材料长度变化的百分比[3]。对于固体物质来说，表示温度每改变1 ℃时，其长度的变化与其在0 ℃时长度的比值。

假设所研究贮箱的材料为5A06 铝合金，其线膨胀系数随温度的变化曲线如图1 所示。因此，对于工作温度的线膨胀系数，应进行差值选取，本文采用3 次拉格朗日差值法。

贮箱在各处均匀的温度载荷作用下，各个部件间的连接处的位移连续且不会产生应力，各几何尺寸发生相同比例的伸缩。由初始温度T0变化到T1后，贮箱体积V 变为

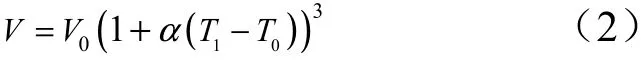
1.2 内压载荷

在内压载荷下，将贮箱（高度为H，半径为r）筒段及前、后底分开考虑，假设贮箱的壁厚为d。在箱筒段处，由平衡方程贮箱箱筒段在内压P 的作用下的轴向应力 σ1和径向应力 σ2分别为

由物理方程可以得到贮箱箱筒段的轴向应变1ε 和径向应变2ε 为

式中E，µ分别为材料的弹性模量和泊松比。

由此可以得到柱段高度变化量和柱段半径变化量分别为

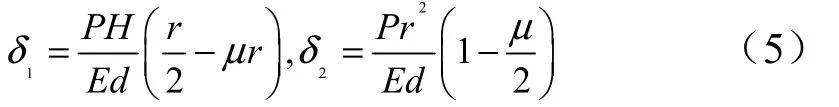
对于前后底，在相同内压的作用下，结构的应力表达式为

同理，可以推导贮箱前后底的变形为

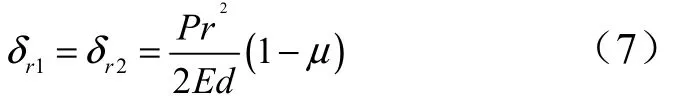
从式（5）和式（7）可以看出，圆筒和半球形封头将在连续处产生不连续位移，不连续量为

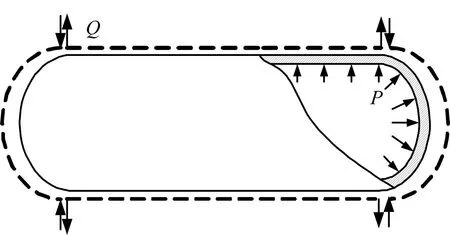
图2 贮箱内压载荷下变形示意 Fig.2 Deformation of the Tank under the Internal Pressure

在实际结构中，这种位移不连续现象是不允许的，因此在半球形封头和圆柱段连接处必然存在圆周均匀分布的剪力 Q，而且其大小恰好消除这种不连续位 移[4]。封头区因为上述原因产生的弯曲应力只对该区域附近有较大影响，所以可以将这一区域当成无限长柱筒的一部分来处理。在算例中，圆筒和封头的厚度相同，在这种情况下可以认为弯矩很小，仅横向剪力Q就使该部分产生相等的变形。根据圆柱壳体的轴对称理论可得：

1.3 轴压载荷

贮箱在前底与筒段连接位置受到轴压F的作用时，对于贮箱筒段来说，其轴向应力1σ 和径向应力2σ 分别为

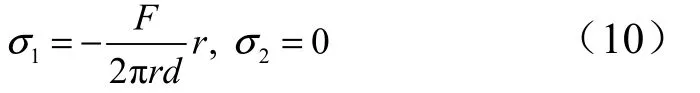
轴向应变 ε1和径向应变ε2为

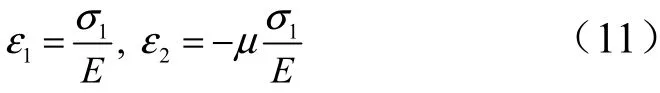
箱筒段的半径变化量 δr为

而由于贮箱前后底与筒段连接位置的变形量为0，同样会产生由于均匀分布剪力引起的不连续量。因此，

同理，圆筒段在连接区域因为剪力Q 引起向内扰度，然而，对应的有相同的剪力Q 将引起球形底向外的挠度，因此由剪力引起的挠度不会导致总体容积的变化。

2 解析方法验证

为验证解析方法的正确性，首先建立如图3 所示的半球形底贮箱的有限元模型。模型半径 r 为2500.0 mm，箱高H 为5000.0 mm，模型各处的厚度d均为5.0 mm，初始温度为15 ℃。有限元模型采用四节点减缩积分壳单元。有限元模型的单元基本尺寸为40 mm。整体模型总计单元约为31 000，节点约为30 000。固支模型筒段与后底连接位置。

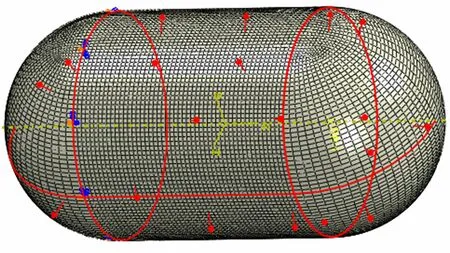
图3 半球形底贮箱的有限元模型 Fig.3 The FEM of the Hemispheric Tank

有限元数值解与解析解法的对比情况如表1所示。

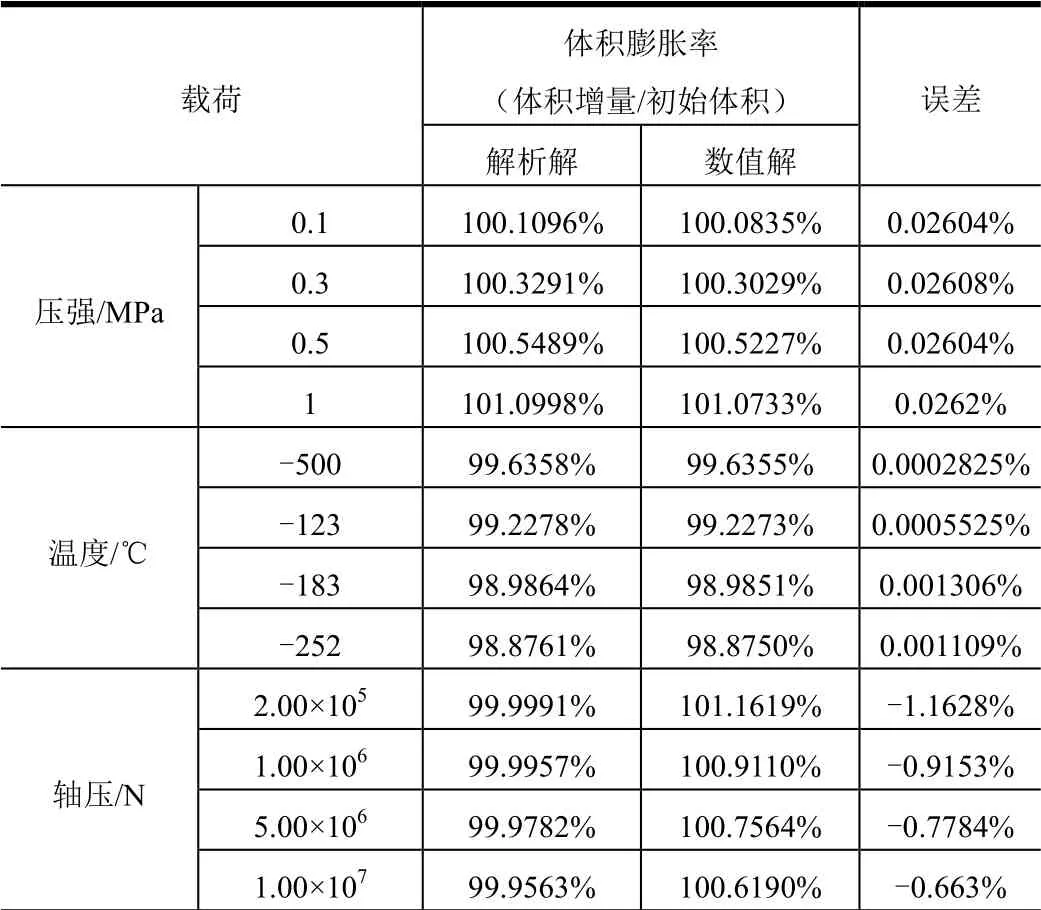
表1 数值解与解析解结果对比 Tab.1 The Comparision between the Numerical Method and the Analytical Method

由表1 结果可见，在温度载荷作用下，解析解和数值解之间的误差小于6×10-4%；在压强作用下，数值解和解析解的所得结果误差在0.03%以下；轴压作用下，数值解和解析解的所得结果误差在1.5%左右。而从量级上看，压强与温度是贮箱变形的主要因素，因此解析解有效、可靠。

3 测量方法

3.1 平面视觉测量原理

空间一点经过成像系统后，与图像坐标系存在一组映射关系，当不考虑景深方向只考虑平面成像关系时，物空间平面物点与像空间成像点存在唯一的映射关系，这种映射关系由相机图像传感器参数和镜头参数唯一确定[5]。平面视觉测量原理如图4 所示。

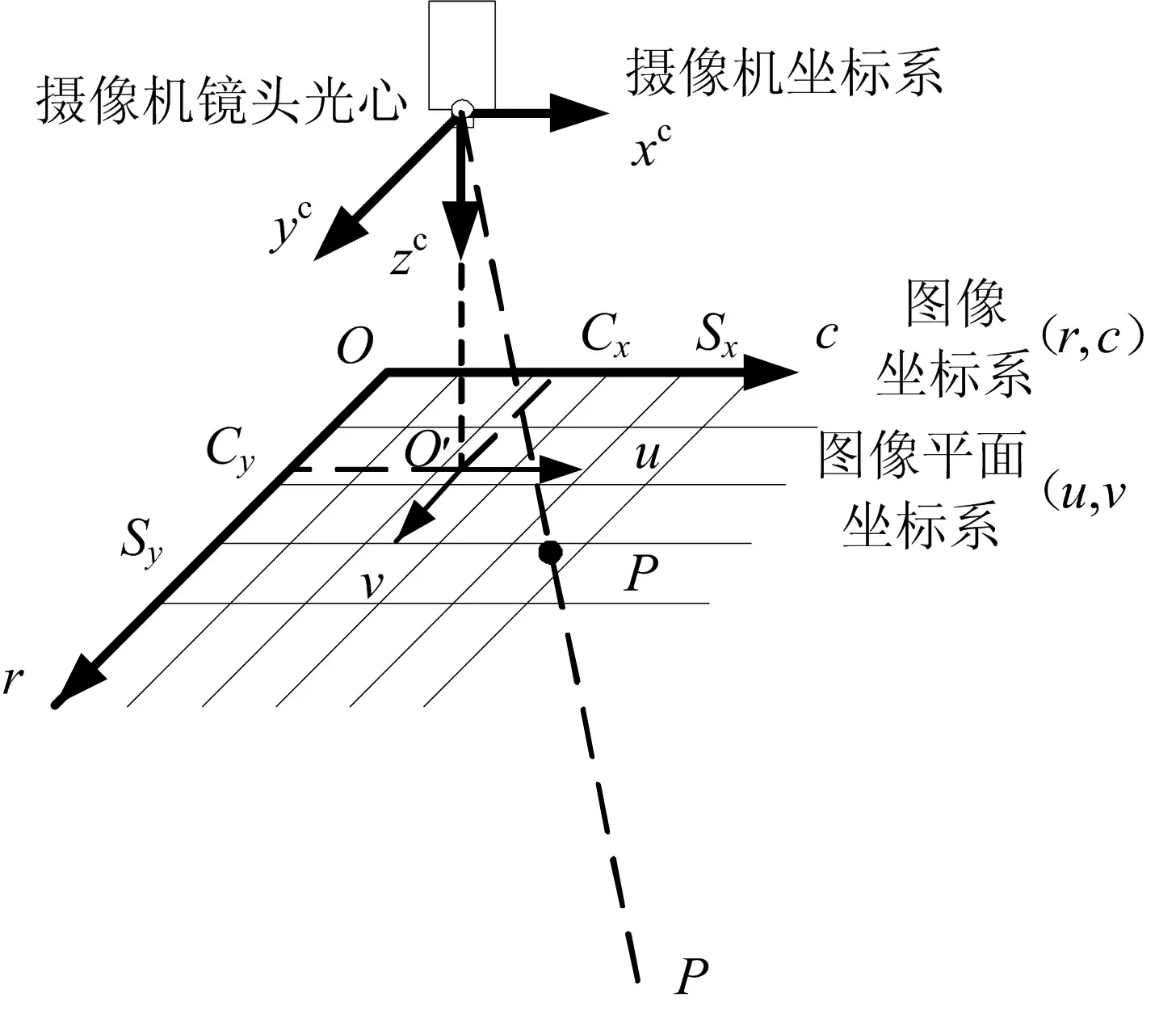
图4 平面视觉测量原理 Fig.4 Schematic Diagram of the Graphic Vision Measurement Principle

在图4 所示的测量原理图中，相机的坐标系为xcyczc，其中 xc、 yc分别与相机图像传感器的行和列平行， zc与相机光轴平行。假设相机成像为小孔成像，经过三角变换后得到虚拟图像坐标为uO 'v。

平面单目视觉测量就是对相机图像传感器参数和镜头参数进行标定。包括相机图像传感器当量因子标定，相机主点位置标定和相机物距标定等方面，上述参数标定涉及到式（14）的旋转矩阵变换和式（15）的缩放矩阵变换：

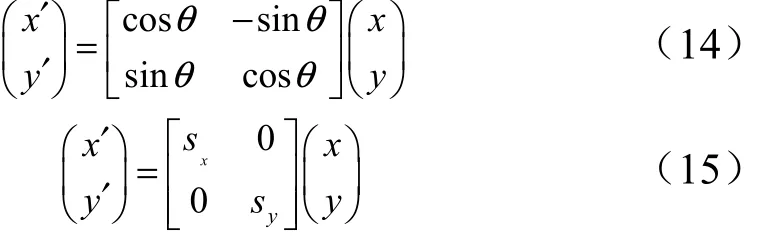
3.2 视觉畸变的非线性校正

在计算机视觉领域中，摄像机的线性模型是针孔模型，但实际的镜头并不是理想的透视成像，且带有不同程度的畸变，使空间点所称的像并不在线性模型所描述的位置。在上述的矩阵变换中均不含有镜头畸变因素，需要增加非线性畸变项xδ 和yδ ，即：

相机的视觉畸变分为3 种情况，分别为径向畸变、离心畸变和薄棱镜畸变[6]。研究表明，引入过多的非线性参数往往无法提高测量的精度，因此一般情况下，径向畸变就足够描述非线性畸变。

径向畸变能够使图像点相对理想位置发生向内或向外的偏移，又称为对称的径向失真[7]，如图5 所示。

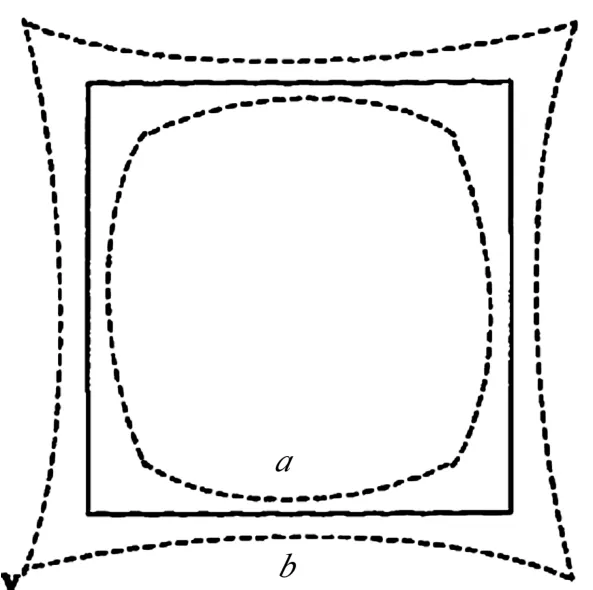
图5 径向畸变模型 Fig.5 Distortion Model in the Radial Direction

这种畸变主要是由于光学系统的镜头径向曲率变化引起的，有正负两种偏移效应，分别称为桶形畸变和枕形畸变。由于径向畸变相对于光轴是对称的，在忽略高阶项的情况下，靶标形心像面偏移量可表达为

式中kl为镜头的径向畸变率。

4 贮箱变形量测量试验

在某运载火箭试车过程中，基于平面视觉原理开展了变形量测量试验。运载火箭推进剂贮箱自上而下分别为氧箱和氢箱，分别布置多个变形量测点。某截面上，变形量测量曲线如图6 所示。测量结果与解析计算结果进行对比，结果如表2 所示。

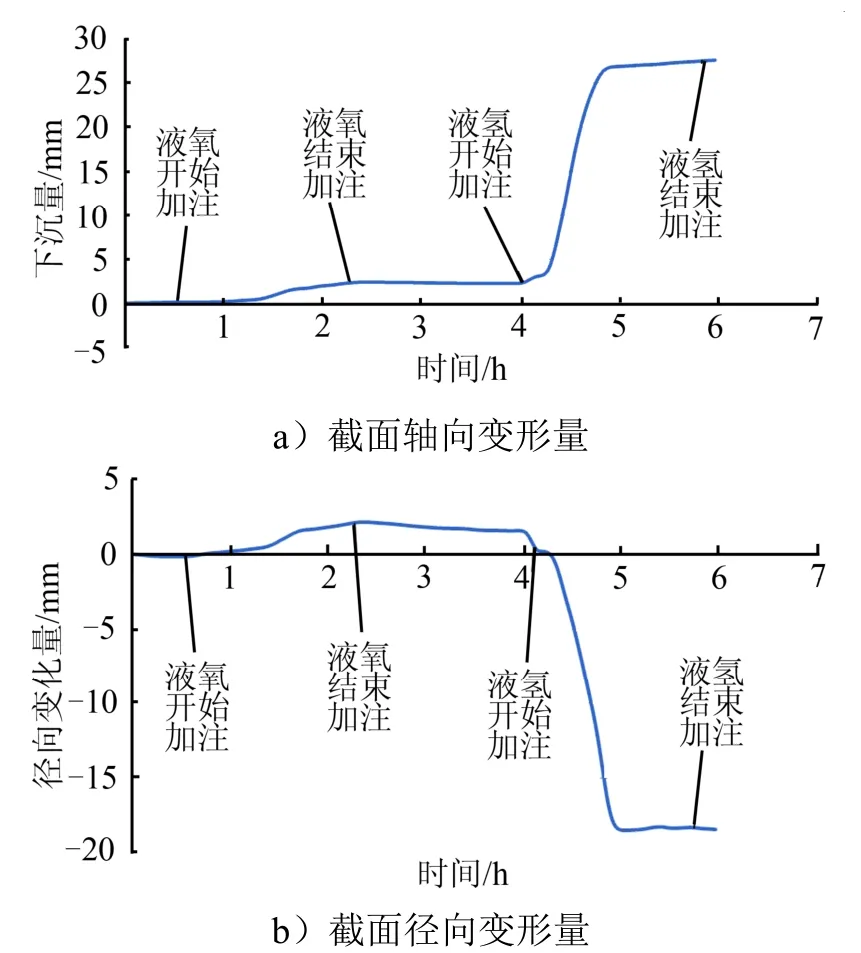
图6 截面变形量测量结果 Fig.6 Measurement Result of One Section

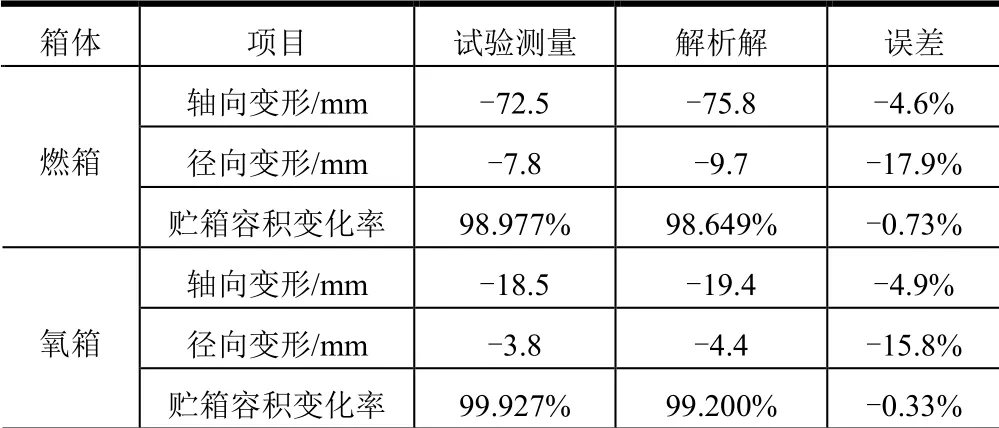
表2 贮箱变形量结果对比 Tab.2 Comparision Result of the Tank Deformation

由表2 可知，理论计算与试验测量结果的一致性较好，在轴向方向上两者误差在5%以内，径向方向误差控制在2 mm 以内，且计算变形量均偏大，对于工程研制来说更加可靠。

另外，两者轴向变形量更加接近，由于管路的补偿量设计更加关注箭体轴向[8]，因此本文的理论计算方法能够作为补偿量设计的依据。

5 结 论

低温运载火箭加注后的变形补偿量设计是箭体结构和管路系统设计的关键输入条件，其合理性直接关系到飞行任务的成败。本文通过理论方法对半球形底贮箱的变形量进行了研究，并基于平面视觉原理研究大尺寸运载火箭的变形量测量方法，通过结果对比分析，验证了理论方法和测量手段的合理、有效性，主要结论如下：

a）线膨胀系数与结构温度有关，应选择合理的插值方式进行选取；

b）压强与温度是低温贮箱变形的主要因素，本文提出的解析方法与数值结果一致性较好，其中温度载荷的误差小于6×10-4%，压强载荷的在0.03%以下，因此能够在满足工程研制需要的前提下，提高计算效率；

c）平面视觉原理测量需要考虑非线性畸变因素，而其中的径向畸变是最为关键的设计因素；

d）通过对某型号运载火箭测量结果与理论计算结果的对比表明，在轴向方向上两者误差在5%以内，径向方向误差控制在2 mm 以内，且均以计算变形量偏大。鉴于管路的补偿量设计更关注箭体轴向变形，因此本文的理论方法能够作为运载火箭补偿量的设计依据。