基于模拟退火算法的元器件布局优化设计

沈 博，潘忠文，林 宏，李文钊

（北京宇航系统工程研究所，北京，100076）

0 引 言

电子设备一般含有众多精密的电子部件，为满足特种需求，需要安装在特殊平台上使用。当电子设备在经受平台输入的振动等力学环境作用时，其印制电路板（Printed Circuit Board，PCB）基板发生较大的动态弯曲变形，这是导致电子设备失效的重要原因。如果在设计中能预估PCB 基板在振动作用下的应力，并对元器件的布局进行优化，降低元器件管脚部位的应力值，便能改善PCB 板的力学环境，提高产品的可靠性。

传统的通过振动试验进行动力学分析的手段不仅耗费成本及时间，同时也难以把握电子系统内部元器件结构特性变化，而有限元仿真可以有效弥补上述缺陷。因此在优化时，往往通过有限元仿真进行验证。朱继元[1]等通过对固有频率计算式的分析，得到应当尽量把大而重的元器件在靠近约束的地方的结论。马静[2]通过计算元器件5 种典型布局下的结果，分析得到了合适的布局方案。黄展达[3]提出了3 种基于刚度扩散法的新方法用于解决不同类别的结构布局优化问题，但只研究了矩形组件的情况。

由于板上元器件数量较大、可调位置较多，一般情况下无法对所有情况进行遍历寻优。往往先通过计算多个典型位置下的模型结果，进行比较分析，从而提出对其布局优化的意见。但由于受到典型位置选取不全的限制，优化结果往往不是最优的。近年来，智能优化算法得到重视，它能克服传统优化算法的局限性并实现全局寻优[4～6]。李晔[7]等用微元体热平衡法建立了电子系统热分析求解温度场的数学模型，采用蚁群算法根据数学模型进行优化，最后通过仿真进行验证。刘孝保[8]等对ANSYS 进行二次开发，采用遗传算法改变板上元器件的布局，对整体的模态频率进行了优化。

在对电路板上元器件的位置进行优化时，智能优化算法中的遗传算法、蚁群算法等都可以使用。但本文优化过程的控制变量，即优化的元器件只有一个，无法凸显遗传算法及蚁群算法多维的特点。相比之下，针对此类问题，模拟退火算法（Simulated Annealing，SA）更易编程实现，且不影响计算效率。因此本文采用模拟退火算法，在有限元仿真计算的基础上对元器件的布局进行优化。在优化模型的求解中，提出改进的模拟退火算法，并采用参数化建模的思想，实现了MATLAB 与NASTRAN 的交互寻优，达到优化元器件布局、改善力学环境的目的。

1 电路板有限元仿真

本文以某电子设备中的电路板为研究对象，采用有限元软件PATRAN 建模。构建模型时，PCB 板以面单元的方式构建，采用四节点板壳单元（Quad4）进行建模，板上元器件采用对面单元拉伸成体单元（Hex8）的方式进行建模。有限元模型见图1。

图1 电路板有限元模型 Fig.1 Finite Element Model

6 号元器件周围布局空旷，可调位置最多，通过优化其布局改善该元器件所处的力学环境的效果最为明显，因此本文重点关注6 号元器件。对于电路板上的其他元器件，同样可以采用本文的方法进行优化，在此不做赘述。

电路板通过螺栓安装在平台上，螺栓连接方式限制了X，Y，Z3 个方向的移动，因此约束为限制模型边界上的全部自由度。根据实际工作情况，电路板受到的载荷来自平台的振动，在模型中螺栓所在位置的节点处施加Z 方向加速度正弦激励，加速度幅值为1g，频率区间为20～2000 Hz，初步设置模态阻尼比为0.01。计算过程中板与元器件均采用线弹性本构方程模型，各部分所使用的材料参数如表1 所示。

表1 材料参数 Tab.1 Material Parameters

2 模拟退火算法及改进

2.1 模拟退火算法

模拟退火算法最早由Metropolis 在1953 年提出，并在1983 年得到发展，Kirkpareick 成功地将其应用于复杂组合最优化问题的求解。至今，模拟退火算法已在工程中得到了广泛的应用，其收敛性理论研究也较为完善。模拟退火算法是通过模仿热力学中的退火过程，以一定的概率选择邻域中的解，以达到全局寻优的目的。整个过程分为加温过程、等温过程以及降温过程。加温过程设定初始温度，作为迭代寻优的起始点；等温过程计算在当前温度下搜索的结果、并判断是否进行更新，判断时采用Metropolis 准则，即满足下列两式之一便更新当前状态的目标函数值：

式中if 为前状态下的目标函数值；jf 为新状态下的目标函数值；kT 为当前状态温度；ξ 为0～1 之间的随机数。

式（2）的目的是在迭代过程中可以跳出局部最优解的情况。降温过程将当前温度kT 从初始温度0T 以一定比例下降到终止温度fT 。降温函数为

式中r 为降温比例，一般为0.9～1，r 越大，温度下降得越慢。通过加温过程、等温过程和降温过程，模拟退火算法最终可以得到目标函数低的优解。

考虑到模拟退火算法的上述特点及优越性，本文基于模拟退火算法对PCB 板上的元器件布局进行了优化，所用模拟退火算法优化参数如表2 所示。

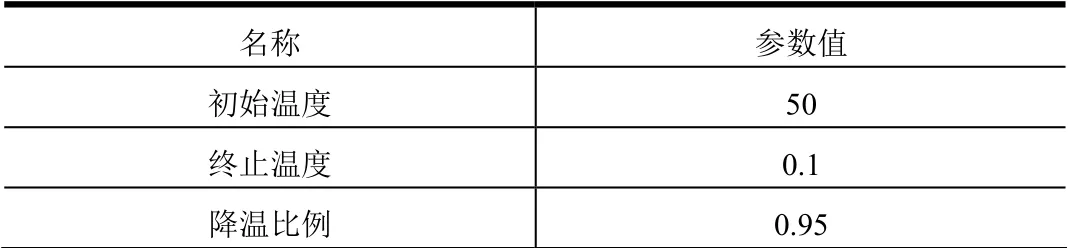
表2 模拟退火算法的优化参数 Tab.2 Optimization Parameters of Simulated Annealing Algorithm

2.2 适应性改进

为使模拟退火算法更适用于元器件的布局优化，在编程时对其进行了适应性的改进，主要有以下几个方面：

a）考虑到程序调用NASTRAN 进行计算时间较长，将每次的计算结果进行存储，避免对同一状态重复计算，可缩短迭代时间；

b）由于每个当前状态的邻域有限，优化过程中记录已搜索的邻域，避免向同一邻域进行重复搜索，可提高收敛速度。

3 元器件布局优化设计

元器件管脚处的加速度及应力值是衡量PCB 板力学环境的一个重要指标。在材料性能符合要求的情况下，加速度及应力值的降低意味着元器件寿命的增长，这对电路板甚至整个电子设备的可靠性都尤为重要。

降低元器件管脚处加速度及应力值的最有效方法为调整元器件的布局。布局优化是对电路板模型的设计与重做。为实现建模的自动化，采用参数化建模的思想，通过对其模型文件内的节点、单元等相关数据进行更改，实现模型的更新。并在此基础上，与有限元计算软件NASTRAN 进行交互，得到新模型的计算结果，从而判断在新布局下目标函数值是否有所降低。

3.1 目标函数

本文选择管脚处的加速度平均值作为优化的目标函数。有限元计算输出文件中包含X、Y、Z 3 个方向加速度的实部和虚部值。先求出3 个方向加速度各自的模长，再计算总的加速度大小。公式如下：

式中a11，a12，a21，a22，a31，a32分别为X、Y、Z 3 个方向加速度的实部和虚部值。

3.2 约束条件

具体约束条件为：

a）与其他元器件距离不小于8 mm，便于元器件的安装；

b）与电路板边界距离不小于3 mm，不妨碍电路板与平台的连接。

3.3 MATLAB 与NASTRAN 交互方法

本文利用NASTRAN 与MATLAB 进行联合编程，既能利用程序实现算法强大的搜索能力，又能实现当前状态的有限元计算，软件交互过程如图2 所示。

图2 交互过程 Fig.2 Interaction Process

优化模型的建立和计算结果的读取都利用MATLAB 编程实现，同时利用NASTRAN 进行有限元计算，输出计算结果。由MATLAB 编程控制NASTRAN计算的输入参数，并读取计算结果，然后产生并输出下一次迭代的元器件位置参数。通过上述循环迭代过程，最终实现优化问题的求解。

现阶段PATRAN 和NASTRAN 的计算过程为：首先使用PATRAN 进行建模，选择分析类型并设置参数，输出为记录了模型节点和单元信息的bdf 文件；然后使用NASTRAN 对bdf 文件进行计算，得到记录计算结果（位移、加速度或应力）的f06 文件；再通过PATRAN 导入结果文件，可将结果可视化并画出曲线。

为使优化过程自动化，避免对建模信息的手动更改，本章使用MATLAB 对原有bdf 文件中模型的节点和单元信息进行更改，通过改变模型的参数实现了模型的重建，改变了元器件的位置，而保证其他元素不发生改变；再在MATLAB 平台上调用NASTRAN 对更改后的bdf 文件进行计算，得到元器件处于新位置时的结果文件f06；最后通过MATLAB 读取f06 文件中的结果信息，画出曲线。这样就在MATLAB 上实现了模型重建、有限元计算、结果读取整个过程，为智能优化算法的使用提供了基础。

3.4 优化结果

在当前网格密度情况下，6 号元器件满足约束条件的可调位置有840 种。若遍历搜索，对所有位置的结果都进行分析计算，按每个位置计算时间约为7 min计算，则所需时间约为98 h，即需要连续计算4 天以上。通过遍历搜索，得到最优解为13.08 m/s2。

采用模拟退火算法对6 号元器件位置进行优化，目标函数的某一次优化过程如图3 所示。由图3 可以看出，开始迭代时加速度值得到大幅下降，随着迭代次数的增加，元器件逐渐向着加速度最小化的方向移动，最终收敛于13.08 m/s2。

图3 应力值优化的收敛结果 Fig.3 Convergence Result of Stress Value Optimization

为验证程序的稳定性，重复运行5 次，记录下每次的运行时间及结果，如表3 所示。

表3 优化结果 Tab.3 Optimization Results

程序平均运行时间为394.4 min，约6.5 h。运行时间的长短与初始解有关，即与随机选择的元器件初始位置有关，而且在优化过程中搜索的方向具有随机性。

可见，采用改进后的模拟退火算法进行搜索寻优，所需时间平均为394.4 min，与遍历搜索相比，时间缩短为原来的1/15，5次搜索的结果中有2次全局最优解，且其余3 次结果的效果并不差。

优化前后的元器件有限元模型如图4 所示。优化后的位置与其他元器件距离均大于8 mm，与电路板边界大于3 mm，符合约束要求。优化后位置与优化前Y轴坐标相同，仅X 轴坐标发生变化，即向X 轴正方向平移11 mm。

图4 优化前后的电路板模型 Fig.4 Board Model Before and After Optimized

优化后元器件管脚处加速度平均值的频响曲线如图5 所示。与优化前相比，优化后加速度平均值的频响曲线峰值得到降低。元器件位于优化前的位置时，管脚处加速度平均值最大为24.0 m/s2；位于优化后的位置时，加速度平均值最大仅为13.1 m/s2，降低比例为45.4%。且频响曲线达到各个峰值时的频率基本不变，说明优化后元器件位置的改变对其模态频率影响较小。

图5 优化前后加速度平均值频响曲线（Z 向） Fig.5 The Mean Acceleration Response Curve Before and After Optimization (Z direction)

计算了优化前后元器件两个位置下管脚处的应力平均值，如图6 所示。与优化前相比，优化后应力平均值的频响曲线峰值得到降低。元器件位于优化前的位置时，管脚处应力平均值最大为0.442 MPa；位于优化后的位置时，应力平均值最大仅为0.155 MPa，降低比例为64.9%。频响曲线达到各个峰值时的频率同样基本不变。可见，根据管脚加速度值进行优化得到的元器件位置，其管脚应力值也得到了大幅降低。

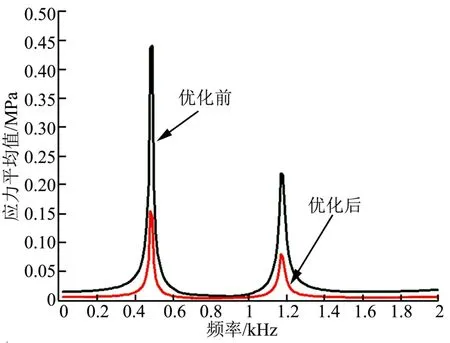
图6 优化前后应力平均值频响曲线（Z 向） Fig.6 The Mean Stress Response Curve Before and After Optimization (Z direction)

4 结 论

本文在有限元建模分析的基础上，利用参数化建模的思想实现了MATLAB 与NASTRAN 的交互，并通过编程实现了改进后的模拟退火算法在元器件布局上的应用，降低了元器件管脚处的加速度及应力值，改善了电路板的力学环境，延长了电子设备的使用寿命，提高了整体的可靠性。优化结果表明，采用的元器件布局优化方法是合理可行的，具有实用价值和推广意义。