展现思考之美

董艳

“深度教学”指引导学习者深层次理解、构建和迁移知识的学习状态和过程。它旨在克服教学过程中表面、表层、表演的局限，引导学生深度学习。深度教学强调站在知识的教育学立场揭示知识的符号表征、逻辑形式和意义系统，提倡通过课程的过程性规约来实现知识的教育价值。

“U型学习”是郭元祥教授对美国著名教育家杜威的经验教学过程理论的概括。郭教授认为，书本具有不可教性，不能直接进行传授，而需要让学习者经历一个复杂的过程，即知识的学习需要经过“还原和下沉”“体验与探究”“反思与上浮”的过程。这个学习过程恰似“U”型，所以将其称之为“U型学习”。

“U型学习”的第一个环节是“下沉与还原”。在数学学习中，学生首先要将课本知识还原为已有的知识背景和活动经验，还原的过程即知识的“下沉”过程。“下沉”环节是对知识进行表征化、表象化和具象化的过程。它一方面有助于学生理解知识的背景和现象，另一方面有助于建立书本知识与学生个人经验的关联性，增强学生对知识的理解。

第二个环节是学生“体验与探究”的过程，即对知识进行自我加工，以及对知识理解、对话、运用的过程。从学习过程的连续性和整体性来看，“体验与探究”环节是学生把知识符号转化为逻辑形式的重要步骤，最复杂、最深刻。

第三个环节是“反思与上浮”，即学生反思和批判性思维的过程。通过反思性思维，将经过自我加工的书本知识进行个人意义的升华和表达，书本知识才能真正变成学生自己理解的东西，即“个人知识”。

如何利用“U型学习”模式提升学生的数学素养和关键能力呢？

一、掠去表象，突出本源，实现理解性学习

与把知识作为孤立的事实来接受和记忆的浅层学习不同，“U型学习”强调理解与批判地接受知识。

在小学数学中，一些性质、规律、法则背后常常蕴含着一般的原理，是一般原理在特定情境中的特殊表现，而这些知识的本质又可以追溯到学生已有的或熟知的经验与观念。在“下沉与还原”中，教师应当运用多种方法探明学生对将要学习的概念或原理的前理解，并运用相应的方法解构学生的“前概念”。

当学生能熟练地背诵结论与方法时，教师应当思索：学生知道了事实是否能真正理解、会背概念了是否能真正理解、会做题了是否能真正理解。《角的度量》是小学数学测量教学中的重难点。教学时，教师通常先教给学生量角的方法，即“点对点、边对边，再定内外圈”，然后反复练习。从实际情况看，这样教学，效果并不理想——部分学生要么总是不会，要么测量的方法单一。

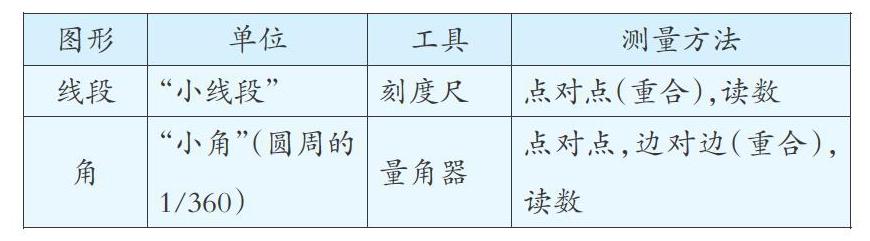
其实，与测量长度、面积和重量一样，度量的本质是相同的：度量时要统一度量单位，再看看度量对象含有几个这样的基本单位（如下表）。

在“探究和加工”的学习过程中，学生体验到角的度量单位是“1o”，所要度量的角含有几个“1o”就是几度的角，这就是度量角的本源。当学生建立了“1o”和“10o”角的空间表象后，教师可以有意识地让学生估角。估角其实是让学生主动利用度量的本源去思考如何量角。经过体验和探究，学生会蓦然发现，计量一个量的多少，其本质是关联的，都是“终点-起点=距离”。

二、抓住关联，注重综合，实现建构性学习

学生探究数学时，不但需要一些基础性、常规性的知识来驱动，更需要从数学整体结构乃至本源上把握数学知识的前后联系。“U型学习”强调从知识的内在结构出发，通过多种方式寻找知识的连接与构建，在不同模型间建立迁移，使学生形成开放的知识结构。

学习《三位数乘两位数的笔算》时，学生从两位数（三位数）乘一位数笔算过渡到两位数乘两位数笔算，再到三位数乘两位数笔算，从知识层面来说是纵向的、统一体系上的知识点，从经验层面来说学生有可以解决问题的口算、估算、笔算的经验。教学中，在学生经历了探究笔算的整个过程之后，教师可以引导他们回顾从“表内乘法”到“三位数乘两位数的笔算”整个知识体系生长的过程，将知识进行系统整理，把零碎的知识点串联成一条线，让学生感知到数学学习是螺旋上升的一个整体。

实际教学中，全课即将结束时，教师让学生猜猜关于“笔算乘法”，小学阶段还会研究什么。学生漫无边际地想到四位数乘三位数、七位数乘六位数。教师微微一笑：“其实在整数的笔算乘法中，小学阶段我们只研究到此。”“遇到位数更多的乘法时怎么办呢？”学生一片愕然，继而顿悟，笔算乘法的核心就是根据“乘法的意义”、利用数的组成及位值原则，只要掌握了这个核心，一切乘法问题均可迎刃而解。

可见，实现“U型学习”既需要教师对知识进行合理加工、有效组织和多样化呈现，又需要学生善于运用学习策略对知识进行积极建构，并内化到个体的认知结构之中。

三、渗透方法，提升思考，实现反思性学习

著名数学家弗赖登塔尔指出：数学思维的发展主要指由较低层次上升到更高层次，如果儿童不能对自己的活动进行反思，他就达不到高级的层次。当前的数学课堂上，教师注重引导学生通过活动来学习，注重理解、对话等学习形式，但由于忽视了深度体验及反思感悟、缺少了“反思与建构”的过程，学习活动常常变得虎头蛇尾。这样自然不能让数学知识、数学经验、数学思想和数学品格等多维目标完整深刻。

在教学中，教师应不断变化知识的表象，引导学生层层深入、不断反思，促使其由表及里地理解知识，增强数学思考能力。

深圳市特级教师黄爱华执教《比较万以内数的大小》练习课时，设计了一组抽签游戏：第一次抽签，从个位抽起（第一次抽到的数字放在个位上，第二次抽到的数字放在十位上，第三次……），哪一队抽到的数字组成的四位数大，哪一队就赢;第二次抽签，从千位抽起（第一次抽到的数字放在4位上，第二次抽到的数字放在百位上，……）;第三次抽签，由抽签者自己决定放在哪一位上。纵观三轮游戏，第一轮游戏的基础是10以内数的大小比较和位置值的认识，这是基点;第二轮游戏的巧妙之处在于“一战定乾坤”，即最高位的数字大小直接决定了两个数的大小，这是发展;第三轮游戏的关键在于对位置值的深刻理解及对数字的直觉把握。

这样的游戏，学生玩得不亦乐乎，可是游戏仅仅是调动兴趣这样简单吗？不。每一轮游戏结束时，黄老师总会追问一句“为什么”。每一个“为什么”都让学生在操作中加深对数位、计数单位、十进制的认识，都促使学生自我完善对数的相对大小的认识。学生在不断地比较中优化、强化对数的理解，进而自主悟出了比较数的大小法则背后的道理。

学生只有在不断地实践、反思中才能深刻理解，才能促进知识从表层符号学习进入知识内在的逻辑形式和意义领域。因此，“U型学习”中的“反思与上浮”不是简单的自我纠错，也不应仅仅理解为课后总结，而应贯穿于学习经历的全过程，成为主体思维活动十分重要的组成部分或基本特征。教学的高境界，不是教会，而是让学生自己悟得。悟，就是在绽放思维之花，展现思考之美。

（作者單位：武汉市洪山区第三小学）

责任编辑  姜楚华