多维度理解地球运动中的难点问题

邢春雷

[摘要]地球运动是高中地理教学的难点内容。在地理教学中，教师可以引导学生从多维度去探究地球运动不易理解的问题，很多内容如果能与数学学科的有关知识相结合，更容易被学生掌握。从多维度分析和理解问题，不仅有利于解决地理学科中地球运动这一难点问题，也有利于解决其它问题。这种思维方式对于学生的终身发展是有益的。

[关键词]多维度;地球运动;数学方法

高中地理中哪部分内容学生学起来最困难？答案毋庸置疑，就是地球运动。地球运动不仅是高中地理教学的重点内容，还是近年来全国卷和各地试卷中的高频考点。为什么学生学起来很吃力呢？通过教学实践我归纳为以下几个原因：

首先，是学生缺乏空间想象能力。高中地理“地球运动”这一部分内容理科性质较强，对学生地理空间思维能力要求极高。对于学生而言，由于缺乏空间想象能力，无法成功地构建脑图，因此对图的判读就不明朗。其次，部分学生对地图的理解能力不强，通过画图、读图，最终掌握地理的思维方式和解决地理问题的能力欠缺。再次，也是最重要的一个原因，就是不善于联系生活实际。地理学习一定要与生产实践相联系，特别是对于地球运动这部分内容而言，很多与生活息息相关的问题都可以通过我们掌握的地理知识去解决，而很多学生却忽略了地理与生活的联系。将地球运动的意义与生活实际相结合，这样不仅可以将抽象的知识具体化和形象化，还可以加深学生对所学知识的印象，最重要的是可以让学生在学习课本知识的同时，找到自然现象发生的根本原因，树立人地协调观。

怎样使地球运动部分的内容简单化？我觉得可以引导学生从多维度去探究地球运动中不易理解的问题。例如，第一个问题：“什么情况下正午太阳高度相等？”要先考虑好该用什么思维去解决这个问题。地理学科最重要的两个要素就是时间与空间，地理现象的产生无非就是时间与空间的结合，所以，看待地理问题我们绝不能忽略时间与空间的重要性。解决上述问题，最好的办法就是把它回归到时间和空间层面上来，再借助正午太阳高度角的计算公式H=90°-|a±b|（a为所求地纬度，b为太阳直射点的纬度），探究同一时间、不同纬度地区有没有可能出现正午太阳高度角相同的情况，同一纬度地区、不同时间有没有可能出现正午太阳高度角相同的情况，这样答案就很清晰了。同一时间，当两个地区的纬度关于太阳直射点对称时，所求地的纬度与太阳直射点的纬度差值是相等的，即正午太阳高度角相同。同一纬度地区，当两个时间关于夏至日或冬至日对称时，太阳直射点的纬度相同，所以，正午太阳高度角也是相同的。

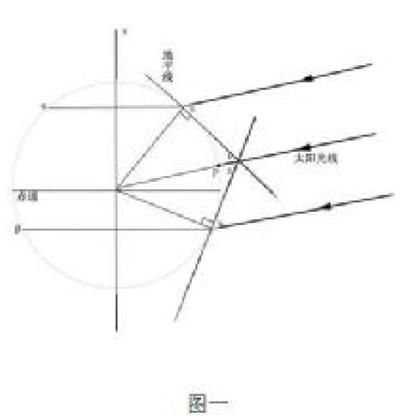
此外，借助数学方法也可以更好地理解这个问题。图一示意两个关于太阳直射点P对称的纬度地区，纬度分别为α和β，它们此时的正午太阳高度分别为H1和H2。那么，数学方法怎样确定两个纬度地区正午太阳高度角相等呢？通过读图我们可以观察，图中有两个直角三角形，它们的斜边是公共边，直角边长度相等，因此它们是全等三角形，所以∠1=∠2，而太阳光线是平行光线，所以，∠H1=∠1，∠H2=∠2，即得到∠H1=∠H2的结论。借助数学知识，我们可以很好地理解关于太阳直射点对称的两个纬度地区正午太阳高度角度的关系。

下面再举一个例子：“为什么北极地区出现极昼时日出日落方向均是正北，日出日落时间是0时？”观察图二，此时北极地区出现极昼现象，点P为晨昏圈与出现极昼现象的最低纬度地区的切点，这个切点同时也是晨昏线与该地的交点，所以点P也代表着出现日出现象和日落现象。我们可以看出经过点P的太阳光线是沿着点P所在经线自北向南照射的，所以对于点P而言，当日出和日落时太阳光线就是正北方向。出现日出和日落现象时的时间为什么是0时呢？我们可以观察点P所在经线的地方时，因为太阳直射点所在经线地方时为12时，点P所在经线与太阳直射点所在经线是两条相对的经线，经度相差180°，所以点P所在经线地方时为0时，即对于出现极昼地区而言，日出日落时间为0时。再者，我们同样可以借助数学方法计算出极昼地区出现日出和日落的时间，根据日出时间=12-1/2昼长，日落时间=12+1/2昼长，因为出现极昼现象，所以昼长取24，我们同样可以得到日出时间为0时，日落时间为24时（0时）的结论。需要注意的是，极昼地区的日出和日落并不是真正意义上的日出和日落。

类似的，我们可以想象一下极夜地区的情况。极夜地区没有日出日落之分，但我们可以考虑它首次迎接日出和日落的时间和方位。如图二所示，我们以点Q为例，当太阳直射点向南移动，Q极夜现象消失，它就会迎来首次日出和日落。日出和日落的时间我们可以通过观察点Q所在经线得到结论，Q所在经线恰好是太阳直射点所在经线，所以地方时为12时，即当极夜地区首次迎接日出和日落时，地方时为12时。同理，运用数学方法：日出时间=12-1/2昼长，日落时间=12+1/2昼长，因为是首次迎接日出，所以昼长很短很短，近似的昼长取0，代入上面式子也可以得到同样的结论。此外，对于像晨昏线上太阳高度角为0°这样很难理解的问题，也是可以通过数学方法解决的。在高中地理教学中，教师不要简单地传授单一的地理知识，而要结合其他学科知识不断丰富地理教学的内容，让学生明白知识的共通性。

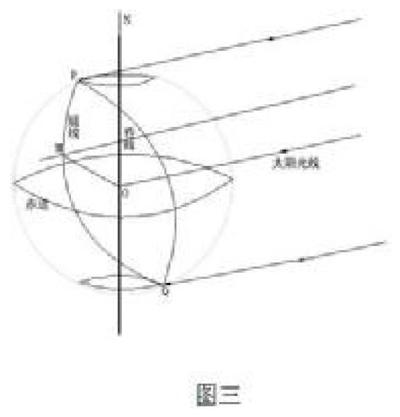
下面我们再看一个问题：为什么晨昏线上太阳高度角为0°？要想理解这个问题，我觉得把数学中的立体几何知识应用到这里再合适不过了。晨昏线上太阳高度角为0°，换句话说，太阳光线与地平线是重合的，怎样证明呢？如图三所示，我们在地表定义一点M，连接地心0与M，过点M作它的地平线，接下来我们运用数学方法来看，太阳光线垂直于晨线，垂直于昏线，所以垂直于晨线与昏线组成的平面，即垂直于晨昏圈，垂直于晨昏圈内所有线段，垂直于OM，所以太阳光線与地平线是平行且重合的。可见，数学方法在地球运动一节中的应用是非常广泛的，要想学好地球运动的相关知识，一定不能把学生的思维固化，必须让他们自己研究，有所创新。

从多维度分析问题，不仅有利于解决地理学科中地球运动这一难点问题，也有利于解决其他问题。这种思维方式对于学生的终身发展是有益的。在教学过程中，教师要注重培养学生从多维度分析和理解问题的能力，从而更好地提高学生的学习效率和综合素质。

参考文献：

[1]鱼建英.用数学对称原理解决地球运动的相关问题[J].地理教学，2015，（04）.

[2]梁莹仪.高中地理“地球运动”教学策略[J].中学教学参考，2017，（13）.

[3]李俊婷.地球运动的地理意义——昼夜长短及其变化规律[J].多媒体教学，2016，（06）.

[4]刘谷.高中地理教育中“地球运动的意义”和生活实际的联系[J].中国校外教育，2014，（01）.

[5]黄彩雯.高中地理核心素养运用之地球运动[J].文理导航，2017，（07）.

[6]许婉英.“地球运动的地理意义”内容详析[J].教材新析，2012，（Z2）.

（责任编辑 赵永玲）