例说解方程在地理解题中的应用

王晓圣

数学中把有未知数的等式叫方程。使等式成立的未知数的值，称为方程的解，或方程的根。求出方程中所有未知数的值的过程就是解方程。

地理中有许多问题需要借助数学解方程的方法求得所需的结论，笔者结合两道试题例说该方法的应用。

例1：图1为“北半球某地的太阳高度日变化图”，读图，求该地的地理坐标是：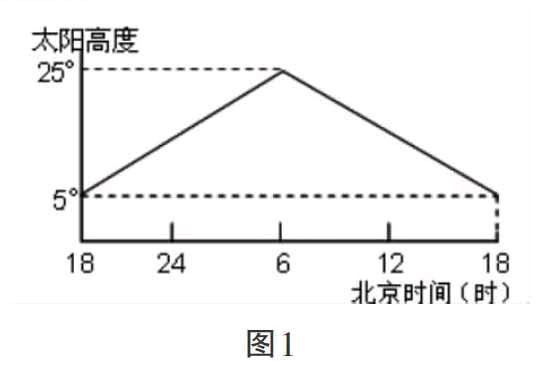

A.70°N

B.80°N

C.150°W

D.30°E

解析：该题要求该地点的地理坐标，即要求出该地的

经度和纬度。

⑴经度求解。图1为坐标示意图：横坐标表示的是北京时间，纵坐标表示的是太阳高度。从图中可以获得：①北京时间为18点时该地太阳高度最小，且最小太阳高度为5°>0，说明该地处于极昼状态；②该地太阳高度最大时（地方时为12点）北京时间为6点；得出：已知该地地方时为12点时，北京时间（120°E）为6点，得出该地位于120°E东侧90°处，（注意经度分布的规律：180°经线东侧为西经度）得出该地经度为150°W。

⑵纬度求解。题干中交代该地为北半球，因该地出现极昼现象，则此日太阳一定直射北半球某纬度，该地一定位于北极圈内某纬度。设太阳直射点的纬度为α，该地的纬度为β，则有式①：β—（90°—α）=5°；从图中还得知：该地的正午太阳高度为25°，则有式②：90°—β+α=25°。解此二元一次方程，得出α=15°N，β=80°N。

例2：表1表示四地一年中昼长最大差值，据此④地的最短昼长为：

A.8小时31分 B.9小时09分

C.10小时42分 D.11小时22分

解析：表1中的数据表示的是①②③④四个地点的昼长的最大差值即最长昼长与最短昼长之间的差。该题原题为两小题，第1小题要求把四地按纬度由高到低进行排列，可根据地球表面各地的昼夜长短变化幅度从赤道向两极随着纬度增大而增大，从而得出纬度由高到低应为：②④①③；而要求出④地的最短昼长可进行文图转换，假设④地为北半球某地，画出简易示意图如图2所示。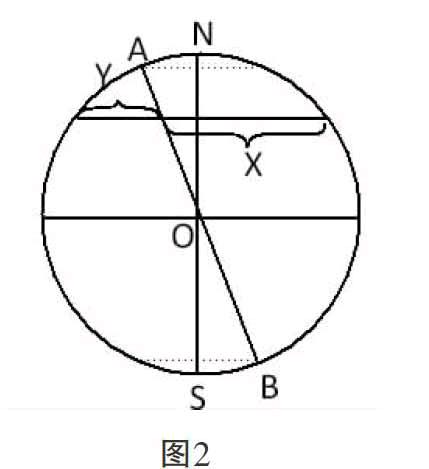

当太阳直射南回归线时，AOB表示昏线，则该地昼长最短为Y；当太阳直射北回归线时，AOB表示晨线，则该地昼长最长为X；由此得出式①：X—Y=5：42；其实还隐含式②：X+Y=24；解此简单方程即可得出该地最长昼长为14：51；最短昼长为9：09

还有很多类似问题，只要巧设未知数，列出简单方程即可顺利解答相关问题，教学中要重视思维训练，注意学科融合，培养运用所学知识解决问题、提出新问题的能力才是教学的本真。