随机利率下参数变化对连续型线性增额寿险的影响
2019-12-13孙嘉聪
沈 丹,孙嘉聪,王 飞
(1. 渤海大学 数理学院, 辽宁 锦州 121013; 2. 辽宁理工学院 信息工程系, 辽宁 锦州121013)
1 给付现值的定义
给付现值,也称折现值,是指把未来现金流量折算为基准时点的价值,用以反映投资的内在价值.使用折现率将未来现金流量折算为现值的过程,称为“折现”.折现率,是指把未来现金流量折算为现值时所使用的一种比率.
2 随机利率下增额寿险模型
2.1 利息累计函数
R(t)=δt+β|B(t)|
(1)
其中B(t)为Brownian运动,|B(t)|是标准反射Brownian〔4〕运动(σ2=1),β也是与t无关的随机变量或常数.
2.2 随机利率下n年定期即时给付增额寿险模型
(2)
其中R(t)为利息累计函数;α>0称为增长系数,特别的当α=1,称为n年标准定期增额寿险〔5〕模型.
3 随机利率下给付现值一阶矩
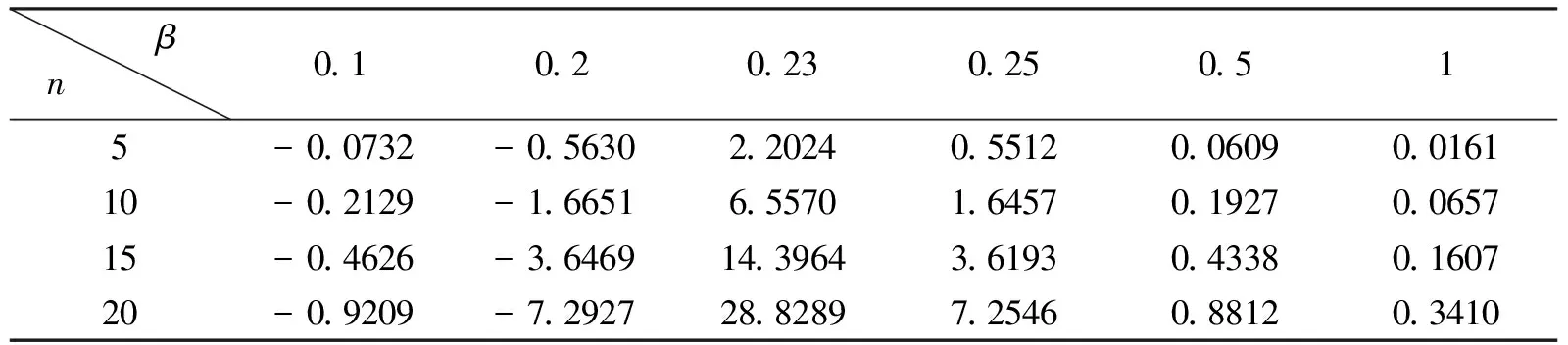
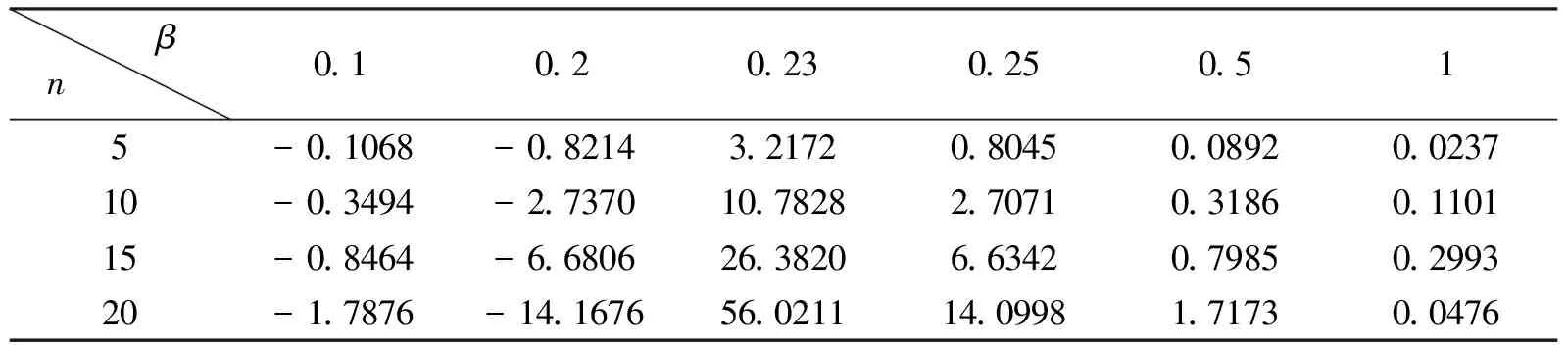
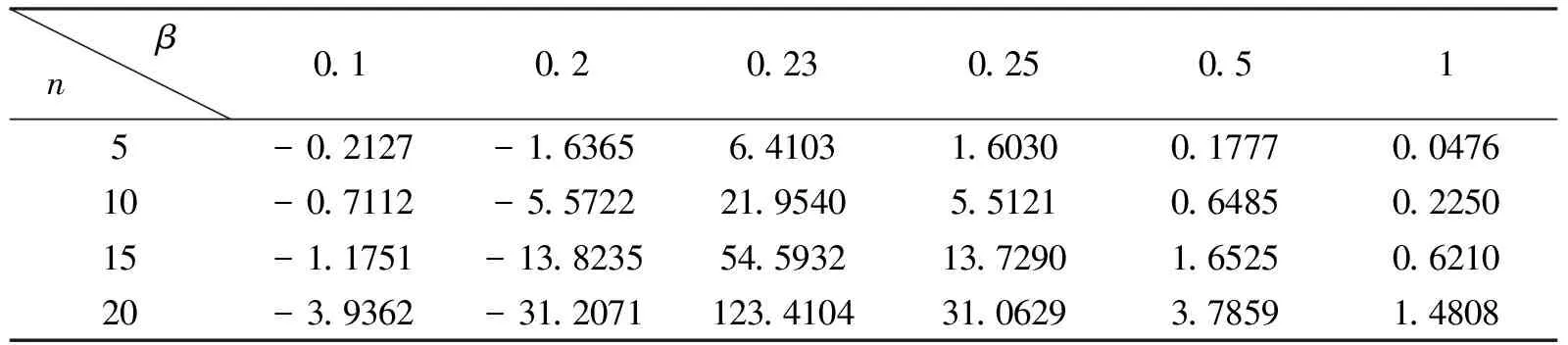
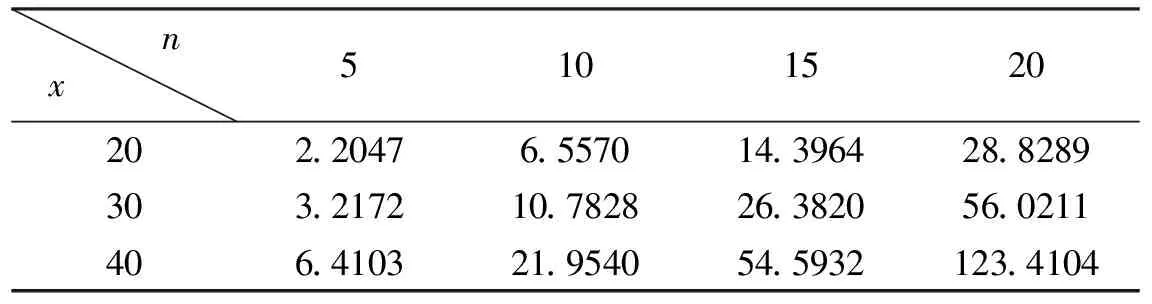
在DeMoivre死亡力下,0≤t 有 ZT=b(1+α[t])e-R(t)=b(1+α[t])e-(δt+β|B(t)|) (3) 即: (4) 考虑5,10,15,20年定期连续型线性增额寿险,假设保费以每年10%递增(α=0.1),令b=1,取银行常见利率δ=0.025代入4中有 若投保人年龄x=20时,β=0.1,n=5 若投保人年龄x=30时,β=0.23,n=10 若投保人年龄x=30时,β=0.23,n=15 若投保人年龄x=40时,β=0.5,n=20 现取参数β=0.1,0.2,0.23,0.25,0.5,1经过MATLAB模拟运算,得到下表 表1 投保人x=20不同参数下给付现值变化表 βn0.10.20.230.250.515-0.0732-0.56302.20240.55120.06090.016110-0.2129-1.66516.55701.64570.19270.065715-0.4626-3.646914.39643.61930.43380.160720-0.9209-7.292728.82897.25460.88120.3410 表2 投保人x=30不同参数下给付现值变化表 βn0.10.20.230.250.515-0.1068-0.82143.21720.80450.08920.023710-0.3494-2.737010.78282.70710.31860.110115-0.8464-6.680626.38206.63420.79850.299320-1.7876-14.167656.021114.09981.71730.0476 表3 投保人x=40不同参数下给付现值变化表 表4 参数β=0.23不同年龄、不同定期下给付现值变化表 根据上述表格有如下结论:当息力累计函数含有Brownian干扰项时, (1)此增额寿险给付现值模型显然为关于增长系数α>0的单调增函数; (2)由表1,表2,表3可知,在参数β=0.23附近给付现值取得最大值.当β>0.23时,给付现值呈现正增长,当β<0.23,给付现值呈现负增长; (3)由表4 在β=0.23处, ①当投保人年龄为20岁时,对应n=5,10,15,20年定期增额寿险,较前一期限下增幅分别为197.41%,119.56%;100.25%. ②当投保人年龄为30岁时,对应n=5,10,15,20年定期增额寿险,较前一期限下增幅分别为235.16%,144.67%,112.35%. ③当投保人年龄为40岁时,对应n=5,10,15,20年定期增额寿险,较前一期限下增幅分别为242.48%,148.67%,126.05%. 可见对于同一投保人,随着时间的增加,给付现值的增加变化趋势先急剧后缓慢. 综上可知,此随机利率下连续型线性增额寿险模型在同一参数下,随着投保期越长,投保年龄越大,回报率越高,有着较强的现实意义与指导意义.4 随机利率下参数变化对连续型线性增额寿险的影响