埃博拉流行病的离散logistic动力学模型及其参数辨识
2019-12-13曹亚丹魏顺行徐恭贤
曹亚丹,魏顺行,徐恭贤*,,2
(1. 渤海大学 数理学院, 辽宁 锦州 121013;2. 渤海大学 数字出版大数据挖掘与治理及呈现技术标准实验室, 辽宁 锦州 121013)
0 引言
埃博拉流行病是一种急性严重传染病,其主要症状初期表现为乏力、发热、肌肉疼痛、头痛和咽喉痛,后期会出现呕吐、腹泻、皮疹、肝肾功能损害,甚至有可能出现内外出血并且严重威胁生命安全〔1-2〕.2014年爆发了史上最严重的一次埃博拉疫情,疫情最先在几内亚发生,由于爆发地对于死者实行埋葬习俗、爆发地人口稠密、疫情国家之间的边贸活动频繁等原因,疫情快速蔓延到其他国家.目前人们对埃博拉流行病的数学建模、传染动力学等方面进行了广泛研究,取得了一系列成果〔1-12〕.
本文研究埃博拉流行病的传染动力学模型建立及其参数辨识问题.首先构建了埃博拉流行病的离散logistic动力学模型,然后给出了参数辨识优化问题,该优化问题可以计算所提离散logistic数学模型的最优参数值.基于世界卫生组织统计的几内亚、塞拉利昂和利比里亚等西非国家的病例数据,拟合出所构建埃博拉离散logistic动力学模型的最优参数值,并对其进行了参数分析.
1 埃博拉流行病的离散logistic非线性系统
目前有多种数学模型可以用来描述流行病的传染动力学〔13-14〕.基于埃博拉传染病的流行特点,本文建立了如下离散logistic动力学模型:
N(t+1)=N(t)+μN(t)-λN2(t),t=t0,t0+1,…,tf-2,tf-1
(1)
N(t0)=N0
(2)
其中,N(t)表示第t天某国家埃博拉传染病患者的累计人数,μ表示染病人数的增长率,λ则表示埃博拉疾病的抑制常数〔1〕,N0表示在爆发初期感染埃博拉病毒的患者数量,t0表示初始染病时间,tf为埃博拉流行病结束的时间.
当埃博拉流行病的染病人数不再上升时,我们有N(t+1)=N(t),称此时的N(t)为最大染病人数,记为Nmax,代入式(1)可得
(3)
染病人数的增长率μ主要取决于埃博拉病毒本身的传染性强弱,而埃博拉疾病的抑制常数λ则主要受疾病爆发后控制措施的合理性和有效性的影响.在埃博拉流行病爆发的初期,由于没有采取有效的控制措施,抑制常数λ趋近于0,此时离散logistic动力学模型(1)~(2)变为
N(t+1)=N(t)+μN(t),t=t0,t0+1,…,tf-2,tf-1
(4)
N(t0)=N0
(5)
其解析解为
N(t)=N0(1+μ)t-t0,t=t0,t0+1,…,tf-1,tf
(6)
2 埃博拉流行病离散logistic模型的参数辨识
为方便起见,记
p=(p1,p2)T
=(μ,λ)T
根据各参数的实际意义可知:参数μ>0,λ>0,初始值N0>0,且μ,λ和N0均为有界变量,即存在
0 0 0 另设 f(N(t),p)=N(t)+p1N(t)-p2N2(t) =N(t)+μN(t)-λN2(t) 则式(1)~式(2)可重新表示为如下形式: N(t+1)=f(N(t),p),t=t0,t0+1,…,tf-2,tf-1 (7) N(t0)=N0 (8) 记某国家第ti(i=0,1,…,n)天的实际累计染病人数为Ne(ti).为了使离散logistic模型(7)~(8)能够较好地描述埃博拉流行病的传染过程,本文以第ti(i=0,1,…,n)天的理论计算值N(ti;N0,p)与实际累计染病人数Ne(ti)之差的平方和为优化目标函数,建立了如下埃博拉流行病的参数辨识问题: (9) s.t.N(ti;N0,p)=f(N(ti-1;N0,p),p),i=2,3,…,n (10) N(ti;N0,p)=f(N(t0),p) (11) N(t0)=N0 (12) p∈P (13) 如果N0给定,则参数辨识问题(9)~(13)是关于参数向量p的连续非线性规划问题.容易证明参数辨识问题(9)~(13)存在最优解p*,即存在p*∈P,使得 F(p*)≤F(p),∀p∈P 以世界卫生组织公布的几内亚、塞拉利昂以及利比里亚三个国家的埃博拉流行病累计感染人数为实际数据(几内亚,塞拉利昂和利比里亚三个国家的数据起始时间分别为2014年3月22日、6月1日和6月16日,截止时间均为2015年12月30日).利用MATLAB软件计算求得三个国家各自染病人数的增长率μ和埃博拉疾病的抑制常数λ的值,(图1、图2).图1和图2也给出了连续logistic模型〔1〕的参数计算结果. 图1 染病人数增长率μ的比较 图2 抑制常数λ的比较 从图1可以看出,三个国家的染病人数增长率μ从小到大排列为几内亚、塞拉利昂、利比里亚.染病人数增长率主要由埃博拉病毒本身的性质决定,但同时也受其他因素的影响,例如国家的地理位置、气候条件、人口数量以及密度、经济发达程度、医疗卫生发展情况、国民身体素质等.通常情况下,国家经济发达程度越高,公共卫生条件越好,则染病人数增长率μ的值就越小.反之,对于经济相对落后的国家,公共卫生条件较差,则染病人数增长率μ的值就比较大.显然,利比里亚的染病人数增长率μ的值甚至大于几内亚的2倍. 从图2可以看出,三个国家抑制常数λ从小到大排列为塞拉利昂、利比里亚、几内亚.抑制常数λ的值显然与人为控制因素有关,抑制常数λ的值越大,说明公共医疗卫生设施更完善,对于传染病的控制和预防更为及时和有效,例如疫苗的及时研发和广泛接种、对感染病人的及时确诊和有效隔离、政府对于疫情的高度重视. 几内亚、塞拉利昂、利比里亚三个国家是西非埃博拉疫情最为严重的国家,三个国家的地理位置彼此邻近,经济发展水平都相对落后,卫生条件都比较差,因此三个国家的染病人数增长率μ以及抑制常数λ的值都在同一数量级之内.三个国家中,几内亚对于埃博拉疫情的重视程度最高,因此与其他两个国家相比,其染病人数增长率μ的值不仅最小,同时抑制常数λ的值也最大,这说明埃博拉流行病的传染在几内亚得到了更好的控制.利比里亚的抑制常数虽然约为塞拉利昂抑制常数的2倍,但由于其染病人数增长率也较大,所以染病人数仍比较大. 图3~5分别表示几内亚、塞拉利昂、利比里亚的埃博拉流行病染病人数仿真结果,可以看出模型计算结果与实际数据之间的拟合度较高. 图3 几内亚埃博拉流行病染病人数仿真结果 图4 塞拉利昂埃博拉流行病染病人数仿真结果 表1给出了几内亚、塞拉利昂、利比里亚三个国家埃博拉流行病的实际累计染病人数以及本文计算出的最大染病人数Nmax和连续logistic模型〔1〕给出的最大染病数Nmax值的比较.从表1中可以看出本文计算出的几内亚、塞拉利昂、利比里亚三个国家最大染病人数和实际累计染病人数的差值分别是31、820和443,而连续logistic模型计算出的三个国家最大染病人数和实际累计染病人数的差值分别是26、857和586.总体来说,本文离散logistic模型的计算值与实际结果更为接近,说明本文的计算结果要优于连续logistic模型的计算结果. 图5 利比里亚埃博拉流行病染病人数仿真结果 表1 两种模型计算的各国埃博拉流行病最大染病人数对比 表2给出了两种模型误差值的对比,从中可以明显看出离散logistic模型计算的三个国家的误差值均明显小于连续logistic模型〔1〕的误差值,进一步说明离散logistic模型比连续logistic模型更接近实际情况,能更准确的描述埃博拉流行病的传染规律. 表2 两种模型的误差值对比 本文研究了埃博拉流行病的传染动力学问题.在前人建立的连续logistic模型基础上,针对实际数据不具有连续性、连续logistic模型不能很好描述实际情况这个问题,建立了离散logistic非线性系统来描述埃博拉流行病的传染规律.以世界卫生组织公布的几内亚、塞拉利昂和利比里亚三个西非疫情国家的埃博拉流行病实际染病人数为数据,运用Matlab软件对构建的离散logistic模型进行了参数辨识研究,计算出各个国家的染病人数增长率和抑制常数的值.结果表明,虽然埃博拉流行病在各国家的传染情况不同,但三个国家的离散logistic模型均比连续logistic模型更符合实际情况,也就是说,与连续logistic模型相比,离散logistic模型能更准确地描述埃博拉流行病在各个国家的传播情况.

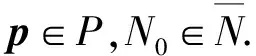
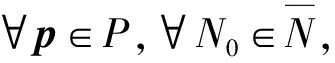
3 结果与分析






4 结论
