航空发动机整体叶盘结构刚度的多目标优化

2019-12-13陈鼎欣简卫斌邓敬亮

航空发动机 2019年5期

陈鼎欣，简卫斌，邓敬亮

（中国航发湖南动力机械研究所中小型航空发动机叶轮机械湖南省重点实验室，湖南株洲412002）

0 引言

随着航空工业的不断发展与工艺水平的不断提升，航空发动机中越来越多地使用整体叶盘结构。该结构不但可以有效减少发动机零件数、减轻转子质量、提高结构紧凑性和发动机可靠性，也能更好避免转接零件连接处气体泄漏，提高气动效率[1-2]。由于整体叶盘集成作功、封严等多项功能于一体，其构造往往相对复杂，涉及的设计参数较多，因此，单纯通过经验和试凑进行结构设计和优化，工作量过大，可靠性也不易保证。陆山、章胜、鲁冯杰等[3-5]采用数值方法或优化算法对2维、3维叶片盘进行分步优化；殷艺云、郭海丁等[6]利用粒子群神经网络对轮盘进行转接位置的局部优化；蔡显新等[7]运用改进的数值方法对叶轮进行形状优化；Riche R L E等[8]采用模拟生物生长的有限元法对简化盘进行外形优化。这些研究均为利用直接数值模型或算法针对叶片盘强度进行优化，且为了保证收敛速度，优化参数通常为5个左右，难以实现优化效率与准确度的均衡，在工程上难以广泛应用。

本文提出1种基于ANSYS平台，通过样本数据集构造响应面，以刚度控制为目标，对多级整体叶盘多个参数进行全局优化的方法。

1 整体叶盘的多目标优化方法

多级整体叶盘优化问题本质上是解决多个相互关联和制约的结构参数分配问题。当结构方案确定，即可将结构参数作为自变量，将强度、刚度和质量等相关函数当作目标函数或约束来处理[9]，由此可将此类问题转化成多目标优化问题。

对于多目标优化方法，目前引入诸如神经网络、遗传算法等进行有效寻优。相对于试凑法，算法优化与响应面优化流程对比如图1所示。直接算法优化由于主要通过仿真计算与算法联动获取结果，优化精度较高，但仿真计算量较大；响应面优化方法以构造响应面为核心，可对响应面筛选寻优结果，工程运用上具有更高的灵活性[10-15]。

图1 优化流程对比

为了获取整体叶盘结构的刚度优化结果，本文在响应面的基础上采用遗传算法进行多目标优化。响应面主要通过运算建立足够数量的设计变量与目标函数之间的试验样本获取。拉丁超立方取样（Latin Hypercube Sampling）相对直接蒙特卡罗法具有更好的均匀分散性，能够充分覆盖设计空间，以较少的试验取点量获得相对较高的数值拟合精度，如图2所示。

图2 试验取样特点对比

本文主要采用拉丁超立方设计获取试验样本。具体优化流程如下：

（1）根据叶片盘具体结构特征确定待优化结构参数、优化目标和控制函数；

（2）试验设计方法采样通过仿真计算获取参数变量与其函数的数据集合；利用数据集合构造响应面，对响应面进行遗传算法寻优，形成基于响应面的预测最优解F1。

（3）将预测最优解点的设计参数代入进行仿真计算，获得目标实际解F2。本文通过式（1）中相对误差E判断寻优结果是否有效。只有预测解接近实际解，即相对误差足够小，才可认为响应面寻优结果有效，否则需要将最优解点代入数据集合提高响应面精度重复响应面优化流程。

2 整体叶盘结构刚度优化算例

2.1 问题描述

研究对象为某型发动机整体叶盘，其材料为TC11钛合金（强度性能见表1）锻件，以轮盘最高工作温度430℃为屈服强度评价温度，插值获得其屈服强度为596 MPa。由于2级叶片数量一致，且经计算，固定叶盘安装边处的位移可以忽略，故剖切出如图3所示的计算模型，并施加位移和循环对称约束，循环对称数为49个。由于气动力对轮盘强度的影响相对较小，故优化中不考虑气动力的影响。轮盘强度评价采用EGD-3标准[16]，即最大等效应力σmax不大于屈服极限，最大径向应力σrmax不大于80%的屈服极限，最大周向应力σvmax不大于95%的屈服极限。

表1 不同温度下TC11合金性能

图3 计算模型及约束

计算获得的叶片盘总变形量与轴向变形量如图4、5所示。由于该整体叶盘采用一端固定，另一端自由的形式，结构刚度偏小，导致其总变形和轴向变形分别为0.626与-0.5466。结构总变形过大，造成工作过程中性能的不稳定与不确定。尤其是轴向变形过大，易造成转子盘与静子件刚性碰摩，其后果更为严重；若在转、静子相邻面留较大间隙来保证安全，则可能破坏流道连贯性，降低气动效率。因此，有必要对叶片盘进行刚度优化，在限制条件下减小结构工作状态下形变量。

图4 总变形分布

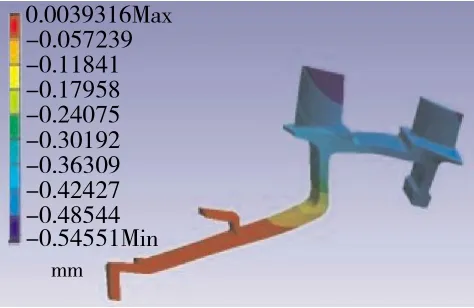
图5 轴向变形分布

2.2 结构刚度参数优化

根据多级整体叶片盘的具体特征（如图6所示），确定模型及其待优化结构参数：对安装位置A与流道相关位置B采取绝对尺寸固定的方式，以确保其在参数变化过程中的位置；对功能结构C采用径向相对尺寸固定，使其在优化过程中结构不变。根据结构的具体特点确定其参数的初值与寻优上下限，见表2。

图6 某型发动机压气机2级整体叶盘结构

表2 设计变量取值

由于克里金（Kriging）代理模型相对在更少样本点下，能够考虑偶然因素的影响，具有较高的局部和全局拟合精度[14]，因而在拉丁超立方试验设计方法取样80组后，采用克里金代理模型获取响应面。控制约束函数见表3。即以EGD-3标准作为应力限制，总质量M增加不大于原方案的15%，最大总变形量Dmax与最大径向变形量Drmax均不大于原方案的。由于轴向变形对工作安全影响最大，且为负值，为使其变形量最小，本文取目标函数为Dzmax最大。

表3 约束条件及目标函数

通过取样并完成响应面的数值拟合后，运用遗传算法对响应面内各点进行适应度评估、选择、交叉、变异，获得预测最优解，并将最优解参数代入计算模块获得真实解。如果预测的约束函数值与实际差别过大（本文取相对误差为1%），则将计算点带入样本点细化响应面继续预测，直到预测值与实际值基本一致。经过13轮响应面细化迭代，遗传算法对轴向点变形最大值与对应质量的遗传算法寻优点如图7所示。获得最后结果见表4。

图7 遗传算法寻优点

从图7中可见，由于结构本身限制与其他函数限制的原因，寻优点并不能达到质量限制值（增加质量15%），使最终获得的变形量最小值不到0.3889。由表4可知，通过刚度优化，整体叶盘轴向最大变形相对减小28.8%，最大综合变形减小15.8%，总质量增加10.5%，其他控制条件均有一定裕度。

定义局部敏感度为

式中：Vi(Xm)max、Vi(Xm)min、Vi(Xm)ave分别为函数在 xm寻优范围内的最大、最小以及平均值，若Vi(Xm)在取值范围内有增大的趋势，则取值为正，反之为负。

局部敏感度反映了引起响应变化的输入变量的权重，正、负值分别表示正、负相关。

各限制函数在克里金代理模型响应面下参数的局部敏感度如图8所示。从图中可见，对轴向变形量的减小影响最大的3个变量分别为HH、R1、A，其中HH、R1受其他限制条件正相关的约束较明显，A仅与σrmax有较明显的正相关限制，而实际σrmax裕度充分（由表4可知），故可针对参数A改进设计以充分发挥结构刚度潜力。

图8 响应面下参数敏感度对比

2.3 改进设计优化

初始优化状态与改进设计状态对比如图9所示。从图中可见，由于左侧所示位置倒角结构限制，使角度A不能进一步增大，因此将该位置结构线条拉直，并倒角光顺，进一步提出改进设计结构方案，使角度A能够在30°～35°寻优，优化参数如图9右侧图所示。

图9 结构优化方案

表5 优化结果对比

通过利用第2.2节方法对改进结构方案参数进行多目标优化，获得其最优结构参数。改进结构与初始结构的控制函数值对比见表5。从表中可知，优化前、后最大应力变化不大，均控制在应力约束范围内；改进优化在初步优化的基础上，综合变形和轴向变形均有进一步改善，相对初步优化，轴向变形与综合变形再减小5.8%与3.8%，径向变形在优化前、后基本保持不变，总质量仅比初始结构的增加14.2%。

初步优化与改进优化的叶片盘综合变形与轴向变形如图10、11所示。从图中可见，改进设计并没有改变叶片盘整体刚度特性分布趋势。在同一工作状态下，改进设计较好地增强了叶片盘刚性，叶片盘位置相关变形量都有一定程度减小。第1、2级叶片盘前端轴向变形分别减小到0.270与0.315以下，基本达到预期优化目标。