某镍基单晶高温合金塑性变形与失效分析

李林骏 ，胡绪腾 ，宋迎东 ，2，孟卫华

（南京航空航天大学能源与动力学院1，机械结构力学及控制国家重点实验室2，南京210016；中国航发湖南动力机械研究所3，湖南株洲412002）

0 引言

镍基单晶高温合金具有良好的高温性能，广泛应用于高性能航空发动机上[1-2]。然而，镍基单晶合金具有宏观各向异性的特点，其塑性变形与失效分析一直是难点。目前，用于分析预测镍基单晶高温合金受载变形行为的方法大致分为宏观唯像法与细观晶体塑性理论2类[3-6]。晶体塑性理论必须考虑单晶材料的滑移规律，而滑移规律十分复杂，且该类理论用于分析3维问题时，在数值积分上具有较大难度，因此在工程应用中受到较大限制[7-8]；宏观唯像法以Hill模型[9-10]为代表，在von mises模型的基础上，通过引入各向异性参数，可以对正交各向异性材料进行力学行为分析。此类模型较为简便，广泛应用于工程实际中，许多学者对此模型进行了修正与改进。丁智平等[3]通过增加1项由应力偏张量分量的2次乘积项构成的应力不变量，对Hill屈服模型进行修正，能够较好地预测出拉剪耦合效应的影响；赵萍等[11]通过在Hill屈服准则中加入含有剪切应力的项对初始Hill屈服准则进行修正，修正后的模型能够对DD3单晶的[001]、[110]、[111]3个取向的屈服应力进行较为准确地预测；C.F.SHIH等[12]细化了表征屈服应力取向依赖性的参数，并引入描述拉压屈服应力不对称的参数，提出了广义Hill模型。

以上研究大多集中在对镍基单晶高温合金屈服强度的预测上，并没有考虑屈服后材料的塑性变形行为与材料在复杂应力状态下所能承受的极限载荷预测。随着航空发动机推重比要求的提高，对材料性能的要求也日益提升，仅仅对材料的屈服强度进行有效预测已不能满足工程设计分析的需要。本文基于广义Hill模型，根据某镍基单晶高温合金的室温和缺口拉伸试验数据，采用反衍优化方法建立镍基单晶高温合金的各向异性本构模型，在此基础上对单晶材料缺口试件在复杂应力状态下的塑性变形行为进行分析预测，并结合Freudenthal失效准则[13]对缺口试件的抗拉强度进行预测分析。

1 镍基单晶高温合金光滑与缺口试件拉伸试验

本文对某镍基单晶高温合金光滑平板试件和3种缺口平板试件（np-r2.5、np-r6、np-sn）进行室温拉伸试验，试验件如图1～4所示，图中数据单位均为mm。所有试件的最长对称轴轴线方向与单晶材料的 [001]取向重合。

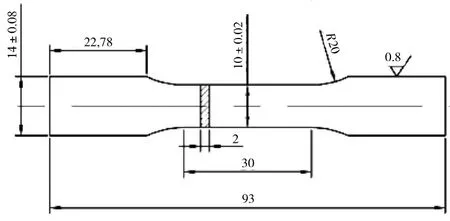
图1 光滑平板件

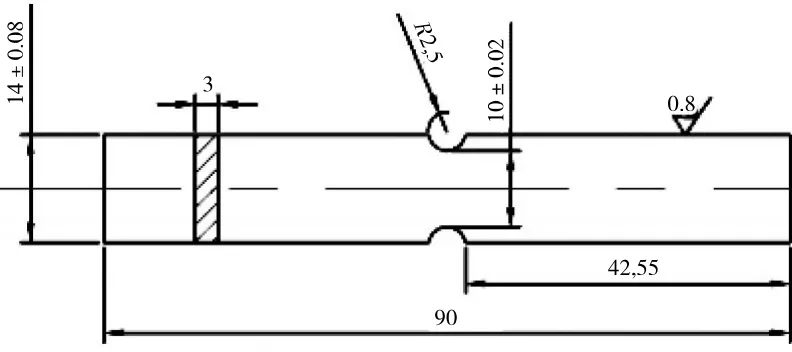
图2 缺口平板np-r2.5

图3 缺口平板np-r6

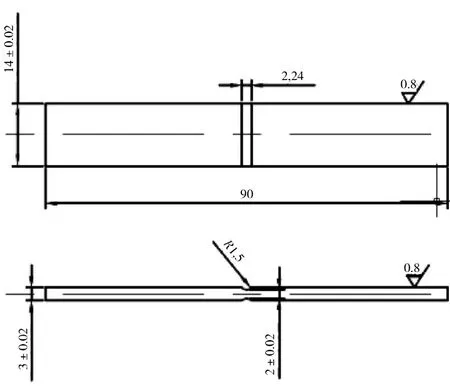
图4 缺口平板np-sn

光滑试件拉伸试验加载速率为0.75 mm/min，缺口试件拉伸试验加载速率为0.25 mm/min，所用引伸计标距均为25 mm，各试件拉伸曲线如图5、6所示。

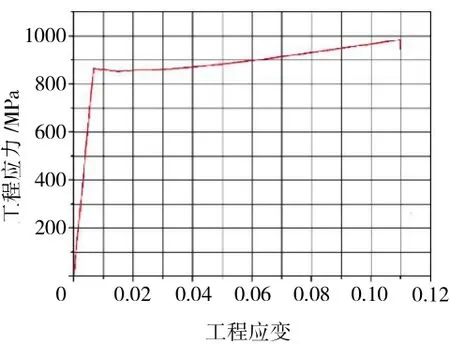
图5 光滑平板拉伸曲线

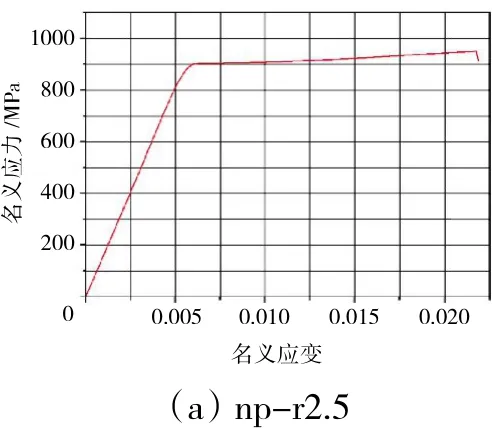
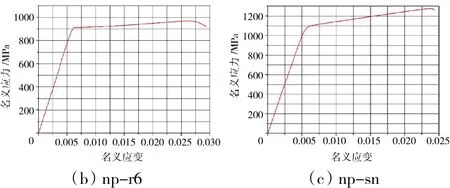
图6 3种缺口平板拉伸曲线

其中，名义应力为试件轴向载荷与最小截面的比值。

从图5中可见，单晶材料[001]向的硬化规律近似为线性硬化，因此，采用双线性模型能够较好地描述[001]向的拉伸性能。

2 广义Hill模型与材料坐标轴的选用

为对单晶缺口试件拉伸响应曲线进行有效地预测分析，需要选用合适的各向异性本构模型，本文选用文献[12]提出的广义Hill模型进行单晶材料塑性变形行为分析。该模型能够对存在屈服应力取向依赖性、拉压屈服不对称性的正交各向异性材料进行有效地塑性变形预测，其屈服准则表达式为

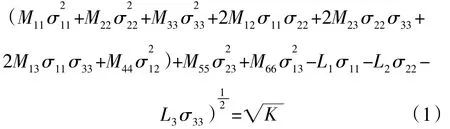
式中：Mij为材料屈服应力取向依赖性参数；Li为屈服应力拉压不对称性参数；K为屈服面大小参数。

各参数关系如下

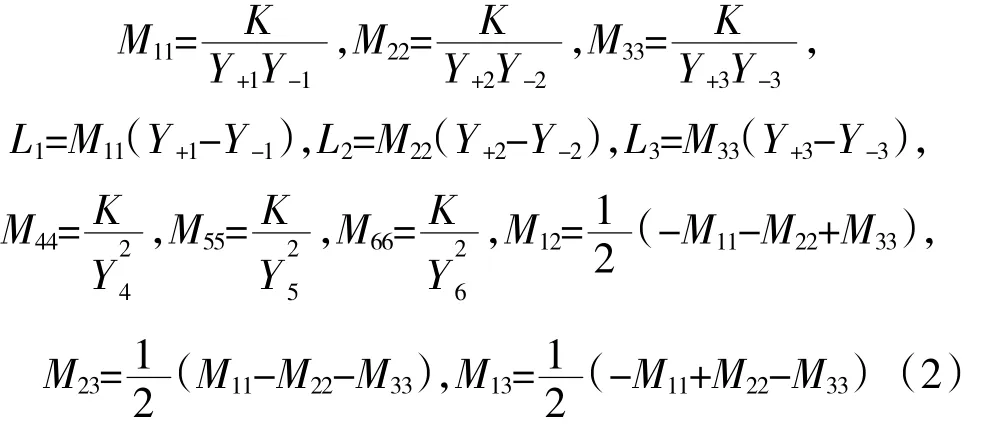
式中：Y表征屈服应力；下标中的数字表示方向，+、-表示拉伸或压缩。

通常令M33=1时，得到

镍基单晶高温合金是1种面心立方的正交各向异性材料，其[100]、[010]、[001]方向具有相同的力学性能，通常研究者都是分别以单晶材料[100]、[010]、[001]3个取向作为材料坐标系的x、y、z轴，这往往导致[110]、[111]方向的性能得不到体现，因此，本文采用材料 [110]、[-110]、[001] 取向作为 x、y、z轴，如图7所示。

由于 [110]、[-110]方向力学性能相同，且镍基单晶合金拉压性能相同[3]，于是可推出

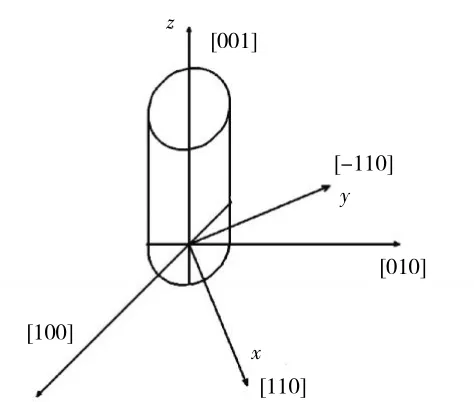
图7 材料坐标轴选取

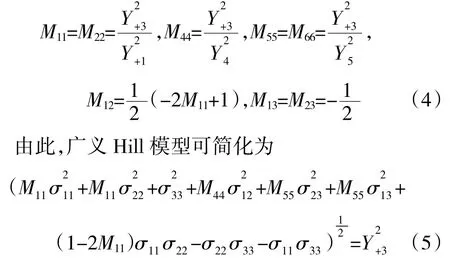
当沿着材料[111]取向方向单向拉伸到屈服时，可由文献[11]中公式推出

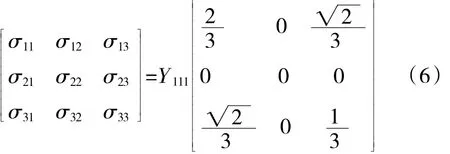
式中：Y111表征材料[111]取向屈服应力，将式（6）带入式（5）可得

由此，[001]、[110]、[111] 取向材料性能都能在本构模型中有所反映。

3 基于反衍法建立各向异性本构模型

3.1 [001]向双线性本构的建立

基于如图5所示的光滑平板件拉伸曲线，将最高点前的工程应力-工程应变曲线转化为真应力-真应变曲线，使用双线性弹塑性本构模型对真应力-真应变曲线进行拟合，以此建立[001]向双线性本构模型。光滑试件拉伸曲线-双线性模型对比如图8所示。

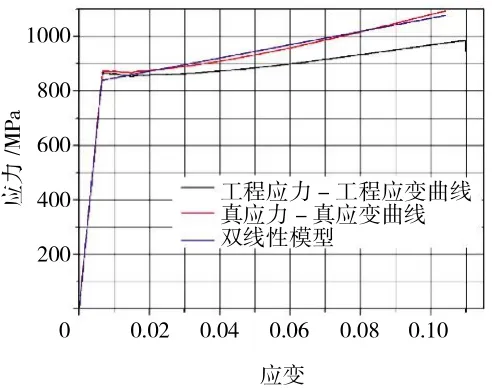
图8 光滑平板[001]向双线性本构模型与拉伸曲线的对比

3.2 非[001]向材料本构参数反衍优化过程

受材料尺寸限制，只能进行[001]向拉伸试验。本文设计了3种缺口平板试件进行拉伸试验，当缺口试件拉伸时，其部位处于多轴应力状态，包含多方向应力信息，利用这一特点，可根据缺口试件拉伸试验结果，反衍出剪切性能及[110]向拉伸性能。反衍法流程如图9、10所示。

最终通过反衍法得到各向异性材料参数，见表1～3。

3.3 金相观测法确定单晶材料[110]取向

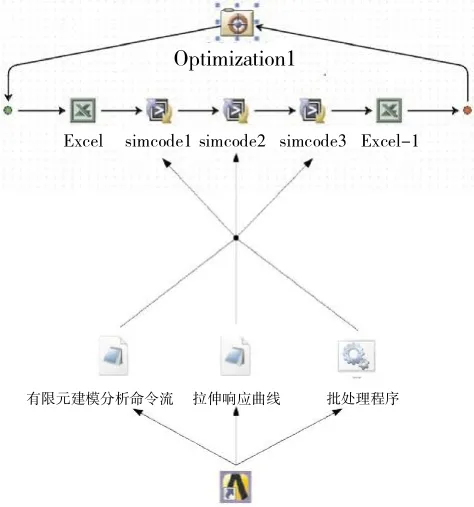
图9 isight反衍优化各向异性材料参数

由于选用[110]、[-110]、[001]方向作为材料坐标系的 x、y、z 轴，因此，需要测定材料的[110]、[001]取向，文中使用的单晶材料毛坯形状为板状，[001]方向为单晶体生长方向，出厂时已经过取向偏离度合格性检测，此处，认为[001]取向与材料长边方向一致，仅需测定[110]取向方向。镍基单晶高温合金在制造过程中必须产生一定的过冷度，而这将会导致材料内部产生许多树枝状的1次枝晶与2次枝晶[14-17]，从垂直于[001]方向的截面进行金相观测，可以观察到呈“十”字枝晶，构成“十”字的为单晶材料的2次枝晶，“十”字2画的方向即为[100]、[010]取向，而与这2个取向夹角为45°的方向即为[110]取向。

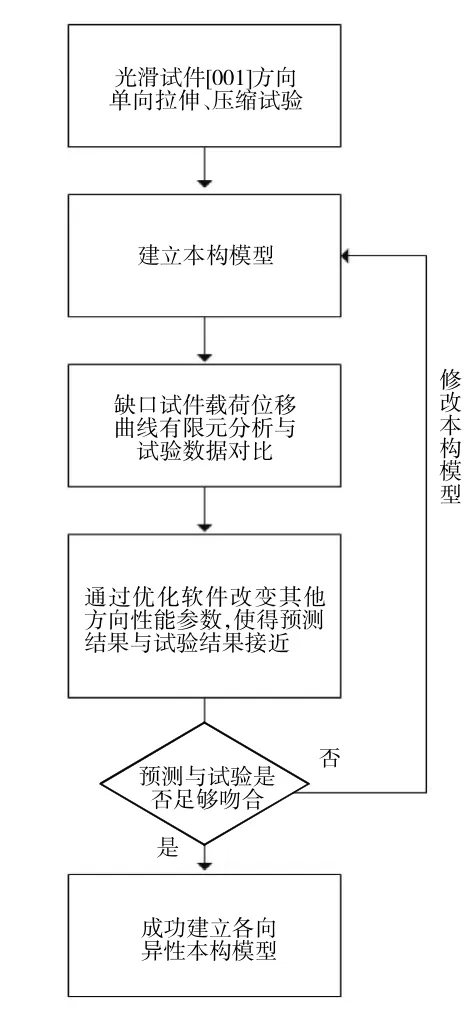
图10 反衍法流程

表1 弹性材料参数

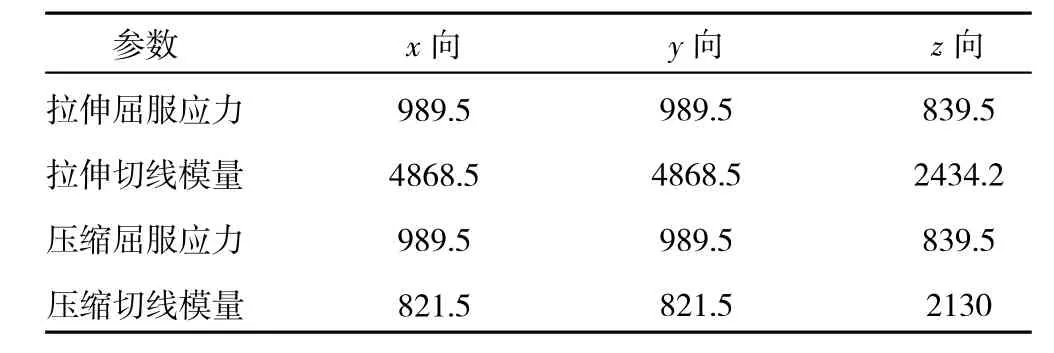
表2 拉压塑性材料参数 MPa

表3 剪切塑性材料参数 MPa

因此，本文通过金相观测的方式进行材料[110]方向的确定，经取样、研磨、抛光后，选用配方为：10 mL HNO3+50 mL HCl+40 mL H2O+20 g CuCl2的金相腐蚀剂对金相样品进行腐蚀，腐蚀方法为：用棉球蘸取少量腐蚀剂，在金相试样表面擦拭2次立即冲洗，即可通过OM观测出试样表面的“十”字枝晶，如图11所示。平板试件垂直于[001]方向的截面上的[100]、[110]取向如图12所示。[001]取向确定后，便可在有限元软件ansys建模时将材料坐标系的x、y轴向转换到[110]、[-110]方向，ansys中单元坐标系与材料坐标系一致，即调整单元坐标系便可完成材料坐标轴的转换，如图13所示。

图11 单晶取向角度测量

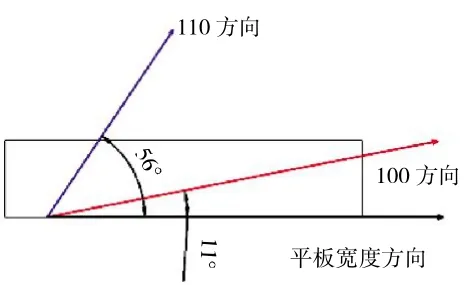
图12 平板试样晶体取向

图13 材料坐标轴转换

4 缺口试件塑性变形分析

基于上述方法建立的各向异性本构模型，针对材料坐标系转换的3种缺口试件有限元模型进行拉伸响应的预测分析，3种试件有限元模型如图14所示。3种缺口平板拉伸响应预测曲线与优化本构试验结果对比如图15所示。

图14 3种缺口试件有限元模型

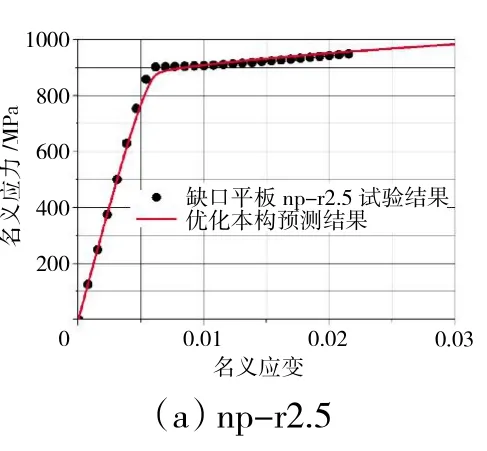
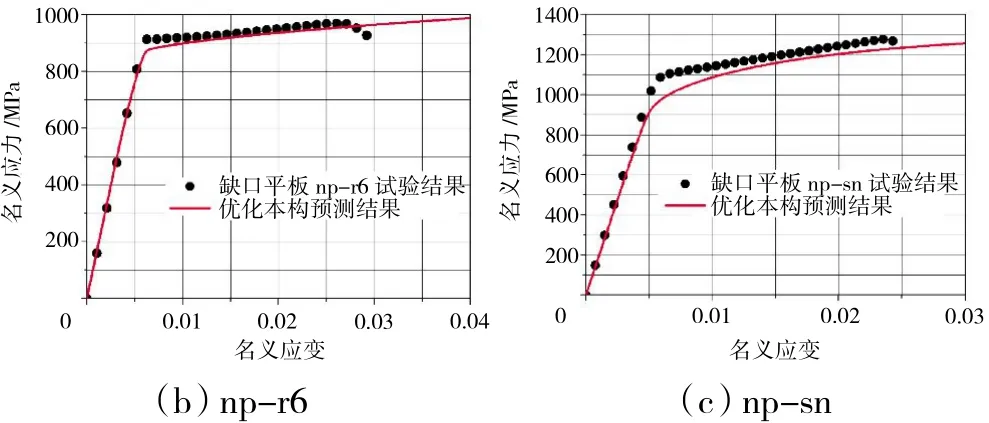
图15 3种缺口平板拉伸响应预测曲线与试验数据对比

从图15中可见，名义应力为端部载荷与试验件最小截面之比，在材料达到名义抗拉强度（极限载荷/最小横截面积）之前，采用反衍法优化获得的各向异性材料本构模型可以较为准确地描述镍基单晶合金材料的塑性变形行为，但预测曲线达到试验失效名义应变时，明显没有下降趋势，这将导致预测的名义抗拉强度远远大于试验值，因此，需要引入失效准则对拉伸响应曲线进行修正。

5 缺口试件失效分析

考虑到广义Hill模型对单晶材料缺口试件的失效行为预测的局限性，通过引入Freudenthal失效准则[13]对上述预测结果进行修正，以提高名义抗拉强度及缺口试件拉伸响应曲线的预测精度。选择缺口平板np-r2.5有限元模型端部位移，达到试验引伸计测量段失效位移时模型的最大塑性功密度作为失效判定阀值，根据Freudenthal失效准则，认为当材料受载后某点的塑性功密度达到判定阀值时，即可认为材料发生失效，各缺口平板最大塑性功密度达到判定阀值时的塑性功密度如图16所示。

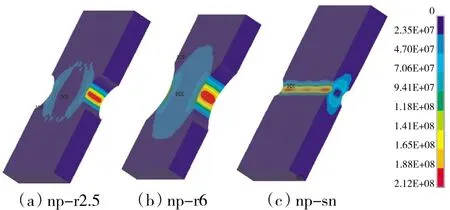
图16 3种缺口平板失效时塑性功密度分布

从图中可见，最大塑性功密度达到失效阀值时，3种缺口的塑性功密度最大值都出现在缺口中心，此处很可能为试件开裂时的裂纹萌生区。通过查找上述云图的试件的端面位移换算成名义应变，即可确定3种试件拉伸响应预测曲线失效点，在此基础上去除拉伸响应预测结果在失效点后的曲线，完成对拉伸响应曲线的修正，修正后的3种缺口试件的拉伸响应预测结果如图17所示。同时也由此确定了3种试件名义抗拉强度的预测值，其与试验值对比见表4。

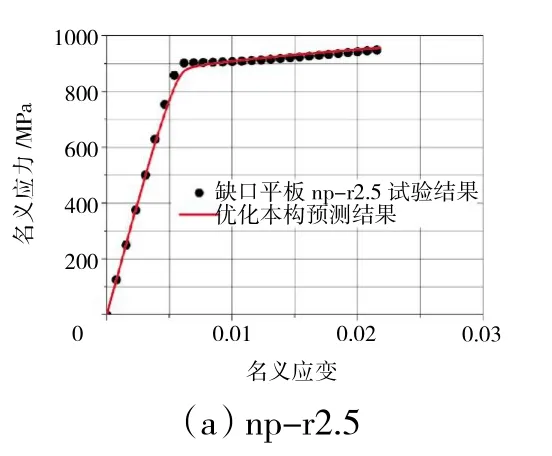
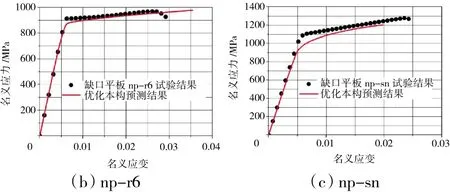
图17 3种缺口平板修正后拉伸响应预测曲线与试验数据对比

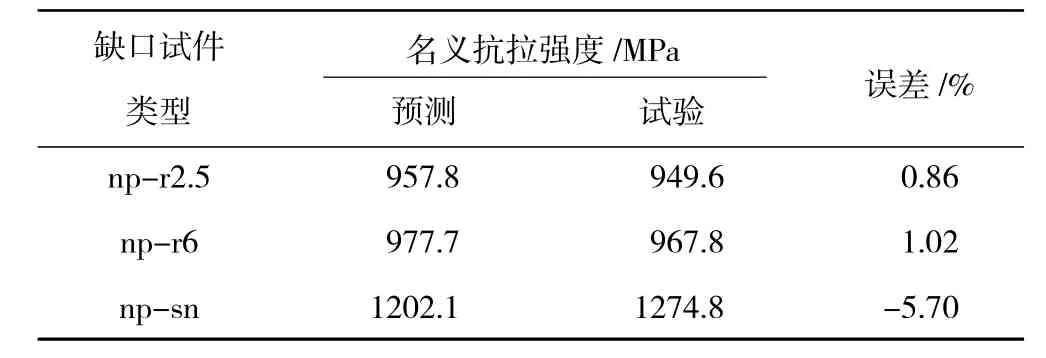
表4 3种试件名义抗拉强度预测值与试验值对比

从图中可见，相较于修正前的预测曲线，修正后的预测曲线明显缩短，失效点更加接近试验值。从表4中可见，采用Freudenthal失效准则，对缺口平板np-r2.5及np-r6的名义抗拉强度预测都高于试验值，误差在1%左右；而对双边侧槽缺口平板np-sn的预测低于试验值，误差小于6%。鉴于以往研究者对镍基单晶高温合金复杂应力状态下承载极限颇有研究，上述预测精度已较为精确。

6 结论

根据光滑平板拉伸试验获取镍基单晶高温合金[001]方向力学性能，经由金相观测法确定材料[110]取向，对材料坐标轴进行转换。基于广义Hill模型及缺口拉伸试验数据，反衍优化获得[110]方向及剪切方向力学性能参数，对3种缺口试件拉伸响应曲线进行预测；基于Freudenthal失效准则确定了3种试件名义抗拉强度，并对拉伸响应曲线进行修正，得到如下结论：

（1）建立的各向异性本构模型能够较为准确地预测镍基单晶高温合金在复杂应力状态下的塑性变形行为，3种缺口试件拉伸响应曲线的预测结果与试验结果较为接近，预测精度较高。

（2）基于Freudenthal失效准则能够较好地预测出3种缺口试件的名义抗拉强度，对缺口平板np-r2.5与缺口平板np-r6预测误差不超过2%，对缺口平板np-sn的预测误差不超过6%，且基于此结果修正的预测拉伸响应曲线，与试验结果具有较好的吻合度。

（3）由于存在一定理论难度，目前无法构建1种与本构耦合的韧性失效准则，无法提升失效点的预测精度，有待进一步研究与发展。