基于EMD模糊熵与会诊决策融合模型的中介轴承故障诊断技术

2019-12-13李有儒刘丽丽李吉凯

航空发动机 2019年5期

王志，李有儒，田晶，刘丽丽，李吉凯

（1.沈阳航空航天大学辽宁省航空推进系统先进测试技术重点实验室，沈阳110136；2.北京交通大学信息科学研究所，北京100044）

0 引言

中介轴承广泛应用于双转子航空发动机支承系统中，由于其工作于高、低压转子之间，润滑较为困难，且随着高、低压转子同时旋转所受动载荷较大，极易发热和过载，从而发生故障[1]，进而可能对飞机的安全运行造成灾难性的危害。因此，对中介轴承状态进行及时而准确的监测，对发生的故障进行准确诊断对于保证发动机安全运行意义重大。

近年来，国内外专家学者针对滚动轴承故障诊断开展了大量研究[2-3]，但在中介轴承故障诊断方面的研究报道相对较少。廖明夫等[4-5]提出基于局部故障边带差值诊断法、转差域频谱和转差域包络谱方法对航空发动机中介轴承进行诊断；艾延廷等[6-7]提出了基于多种信息熵的融合算法，并通过所提出的信息熵距法和过程信息熵融合方法对中介轴承进行故障诊断。以上研究主要侧重于故障特征提取方法的研究，针对中介轴承故障样本小的故障识别算法研究较少。故障识别主要包括信号处理、特征提取和分类器设计3部分。振动信号是航空发动机轴承故障诊断中应用最为广泛的故障监测信号，针对该信号的处理方法研究较为广泛[8]。实现对信号更准确的自适应性分解，从而提取出能够准确反映轴承故障状态的特征参数是特征提取的主要目的，也是故障诊断准确与否的关键步骤。秦娜等[9]使用EMD算法对振动信号进行分解从而提取了有效的故障特征，并对特征进行分类识别取得良好的诊断效果。故障识别实质上是数据挖掘问题，主要通过中介轴承故障特征提取和模型训练算法选择实现。因每种训练算法特点不同，且不同的算法对不同类型数据的拟合能力也不尽相同。传统分类器的设计基于单一的某种分类算法，弊端是分类效果过度的依赖于特征选取和训练集数据的清洁程度，从而使得训练算法具有鲁棒性差、泛化能力低下等弱点[10-12]。

针对中介轴承故障信号传递路径长、信噪比低，具有明显的非线性、非平稳性，诊断困难等特点，本文提出采用经验模态分解（Empirical Mode Decomposition，EMD）模糊熵作为中介轴承故障特征向量，并建立1种基于k-最近邻（k-NearestNeighbor，kNN）、支持向量机（Support Vector Machine，SVM）、决策分类树（Classification And Regression Tree，CART）、随机森林（Random Forest，RF）以及梯度提升决策树（Gradient Boosting Decision Tree，GBDT）5 种机器学习算法组合构成的集成机器学习会诊决策模型对中介轴承故障进行诊断。首先，开展某型航空发动机中介轴承故障模拟试验，采集多转速、多测点振动故障信号，并提取信号的EMD模糊熵构造故障特征向量。然后，形成故障样本并训练所提出的机器学习会诊决策模型，并采用自适应遗传算法优化个分类器权重，对决策结果进行融合。最后，采用会诊模型对中介轴承故障进行诊断，检验模型的泛化能力。

1 振动信号的EMD模糊熵

1.1 基于EMD的信号分解

经验模式分解（EMD）是Huang等[13]提出的1种根据信号自身的时间特征尺度，将其自适应性分解为若干个不同有限个本征模函数（Intrinsic Mode Function，IMF）分量的信号处理方法。因为EMD分解不受基函数的局限，能够准确有效地反映原始数据的微小特征，避免信号能量扩散和泄漏，故相比于小波算法的多分辨率，EMD方法在稳定性和准确性上具有更好的适应能力。某中介轴承在故障状态下采集到的振动信号经EMD分解得到的各IMF分量波形如图1所示。从图中可见，原始信号经过EMD分解后，各IMF分量包含了原信号的不同特征尺度，包含的频段从高到低。由于某些微弱信号可以在IMF分量中突显，因此利用IMF分量进行分析更加准确。

图1 中介轴承振动信号的EMD分解结果

1.2 振动信号的模糊熵

模糊熵[14]是1种对时间序列复杂度进行度量的方法，可以衡量时间序列在发生维数变化时产生新模式的概率大小。中介轴承在正常和不同故障情况下信息复杂程度不同，产生新模式的概率也不相同，因此不同状态的模糊熵不尽相同。模糊熵克服了样本熵和近似熵突变性大和熵值连续性差的缺点。本文采用模糊熵作为中介轴承的故障特征参数，其计算方法如下。

（1）将长度为N的原始序列x组成1组模式长度为m的向量序列

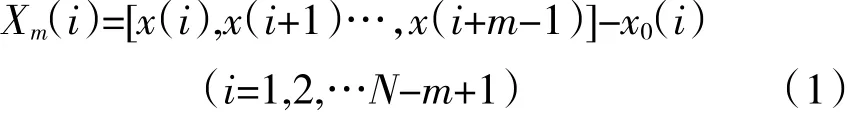
式中：Xm（i）为1个新的时间序列；x0（i）表示m个连续x（i）的均值。

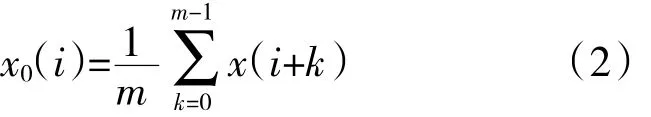
（2）定义向量Xm（i）和Xm（j）的距离为dm（i,j）

（3）采用模糊函数 μ（dm（i,j）,n,r）定义向量 Xm（i）和Xm（j）的相似度Dm（i，j）

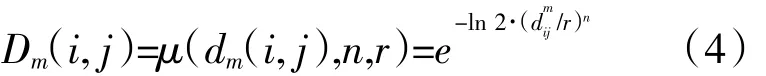
式中：r和n为相似容限和梯度；模糊函数为指数函数。

（4）定义函数

（5）增加维数至 m+1，重复上述步骤（1）～（4）得到φm+1（n,r）

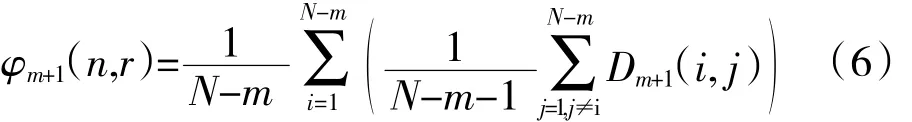
（6）时间序列{x（i）,i=1,2,…,N}的模糊熵可以定义为

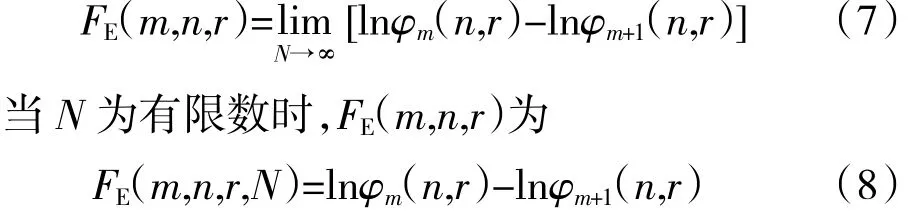
式中：m、r和n的设定是模糊熵计算的主要参数，本文取 m=2，r=0.2s，s为样本的标准差，n=3。

2 会诊决策融合模型

2.1 基于机器学习方法设计分类器

轴承故障诊断多采用基于数据驱动判别式为核心的分类器设计，而机器学习算法是1种高效的分类器设计方法。在机器学习理论中，根据训练集数据有无标签，又可以将其分为监督式学习和无监督式学习。通常意义上通过构建有监督信息的航空发动机中介轴承故障数据集，并使用该集合训练所设计的分类器是基于数据的故障诊断问题的常用解决方案。本文基于此类通用的解决框架，通过优化分类器设计来提高航空发动机中介轴承故障诊断性能。

2.2 会诊模型中的基分类器

2.2.1 k-近邻（kNN）算法

kNN算法[15]是1种基于统计学思想的监督式学习分类算法，其工作机理为：给定测试样本，基于如广义海明距离等某种距离度量方法找出训练集中与之最靠近的k个训练样本，然后基于这k个“邻居”的信息进行相应的预测。本文在处理分类问题中可以使用“投票法”，即选择这k个样本中出现最多的类别标签作为预测结果。该算法可以针对中介轴承故障数据信噪比低的特点，实现野值和噪声的去除并将训练集数据进行归一化处理。

2.2.2 支持向量机（SVM）算法

支持向量机由Vapnik[16]提出并广泛应用于机械故障诊断等分类问题中。该算法最初为2值分类问题设计的，而中介轴承故障诊断为多分类问题。如直接修改目标函数参数，将不同分类平面的参数求解合并归一化存在计算量过大问题。为了解决该问题，采用多个2分类组合成1个多分类器的方法实现中介轴承故障诊断的多分类功能。考虑中介轴承故障诊断结果，并兼顾模型在训练集和测试集上综合的表现，将模型中的惩罚系数设置为10。模型中采用径向基函数（Radial Basis Function，RBF）作为核函数。核函数公式为

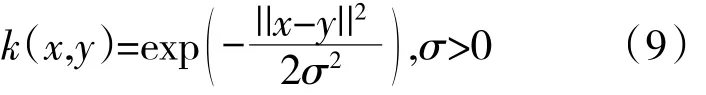
式中：x,y为特征向量；σ为控制函数径向作用范围的宽度参数。

2.2.3 分类回归树（CART）算法

分类回归树（CART）模型基于树结构建立，通常包含1个根节点和多个内部节点和叶子结点。根节点中是样本全集，叶子节点存放分类结果，中间节点对应1个属性测试。中介轴承的故障诊断过程即采集由模糊熵组成的故障数据样本被划分到对应的故障类型的子节点中。训练过程，子节点的样本纯度（包含相同种类样本的比例）不断迭代。本文采用Gini系数进行节点纯度度量，以降低Gini系数为目标进行中间节点的属性划分。Gini系数可以表示为

式中：K为分类数；pk为样本属于第k个类的概率。

2.2.4 集成学习算法

集成学习算法中的挂袋法和提升法是经典的故障诊断方法。挂袋法又称为引导聚集，只有在潜在的模型能产生不同的变化时才有效，即让潜在的数据引入变化，就产生有着轻微变化的多种模型。挂袋法自举产生个不同的数据集，然后对每个数据集构建1个模型。对于分类问题，最后输出的结果取决于投票。Leo Breiman[18]提出的随机森林（RF）算法就是利用挂袋法思想通过改进决策树而形成的1种集成学习技术。构建随机森林的步骤如下：

从1-T进行迭代，构建T棵决策树。

（1）对于每棵树，从输入数据集中自举大小为D的样本。

（2）对输入数据产生出1棵树t：

Step1：随机选择m个属性；

Step2：采用预先定义好的标准，选择1个最佳属性作为划分变量；

Step3：将数据集划分成2部分；

Step4：在已经划分的数据集Step1-Step3；

（3）返回树 T。

Friedman[19]提出的GBDT算法是采用M棵决策树为弱分类器的加法模型，其数学形式表示为

式中：ω0为初始值；Φ（x）为模型的损失函数。

传统提升法将所有样本初始化相同权重，通过迭代过程发现样本的分类差异进而对其权值进行调整，每次迭代都将产生1个弱分类器。最后通过投票或加权等方式产生最后的强分类器。该方法对中介轴承故障信号这种非线性、非平稳信号诊断效率较低。梯度提升表示在模型训练的过程中，为减小残差而在残差降低的梯度的方向上去建立新的模型。使上一个模型的残差在梯度方向上减少，提高中介轴承故障诊断效率。

2.3 会诊决策模型原理

基于机器学习理论中的集成学习方法思想建立机器学习会诊模型。但有别于集成学习算法融合多种弱分类器，针对中介轴承故障信号非线性、非平稳和信噪比低的特点，本文建立的会诊模型融合kNN、SVM、CART、RF和GBDT等5种强分类器。通过对会诊模型中的5种强分类器的决策结果进行融合，抑制信号中的噪声和野值，提高信噪比，提升中介轴承故障诊断效率。

本文建立的会诊模型是基于Bootstrap抽样方法构建与训练样本相同的数据集，基于抽样后的新的故障数据集，训练kNN、SVM、CART、RF和GBDT等5种强分类器。通过统计多个分类器得到的决策结果产生最终诊断结果，同时根据故障诊断结果，采用遗传算法优化5个分类器的决策权重，最终结果优于单个分类器诊断获得的结果，提高中介轴承故障诊断的容错能力，降低误判率。

遗传算法目标函数为

式中：f为会诊模型故障识别准确度；ξi为子模型的准确度；λi为子模型的权重。

遗传算法编码长度选择采用40位长度的二进制码实现。初始种群容量为50，初始交叉概率为0.9，初始变异概率为0.01。

机器学习会诊模型的实现过程如图2所示。

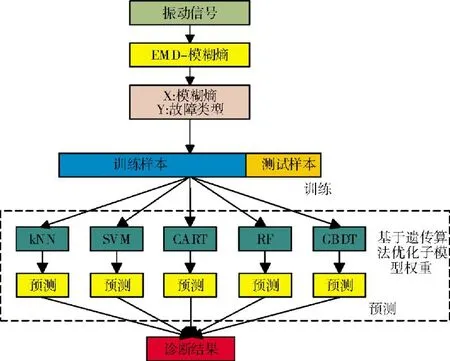
图2 会诊模型决策融合过程

集成学习会诊模型是基于信息融合中的决策融合理论构建的1种信息融合故障诊断模型。该模型区别于现有的同类模型决策融合，是基于Bootstrap抽样方法建立的异类模型的决策融合诊断模型，其融合了以SVM为代表的核模型和以GBDT为代表的树模型，集成了2种类模型的优点。因此，提高了故障诊断的精度和泛化能力。

3 诊断实例

3.1 中介轴承故障模拟试验

为验证机器学习会诊模型在航空发动机中介轴承故障诊断中的性能，开展某型航空发动机中介轴承故障模拟试验，其试验台如图3所示。该试验台能够模拟中介轴承与发动机匣之间的传递路径，其信号复杂程度更加接近发动机实际工作状态。同时在机匣的表面上布置了5个ICP加速度传感器，采用Test.lab数据采集分析系统进行振动数据采集。在试验中采集了不同转速下的中介轴承内环故障、内环-滚动体耦合故障、正常、滚棒剥落、滚棒划伤5种不同状态的振动信号。每次试验采样时间为2 s，采样频率为6400 Hz，每种故障类型试验40次。试验所采用的某型发动机中介轴承为圆柱滚棒轴承，轴承结构如图4所示，轴承参数见表1。

图3 航空发动机中介轴承故障模拟试验台

图4 某型航空发动机中介轴承

表1 中介轴承几何参数

3.2 会诊模型应用于故障诊断

采集信号经EMD分解得到10维IMF分量，按照式（1）～（8）计算出相应的模糊熵作为故障特征，选取前8维特征向量组成特征矩阵。每种状态试验40次，在5种状态下总计200组模糊熵值。最后得到特征矩阵和标签向量

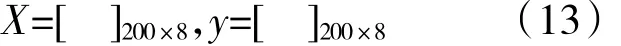
在保证训练集和测试集样本属性分布一致的情况下，划分训练集和测试集的比例大小为80%和20%。最终用160个带故障类别的样本训练会诊决策模型，40个带故障类别的样本测试会诊模型的泛化能力并根据中介轴承故障预测结果的准确率对模型进行评估。部分故障样本见表2。

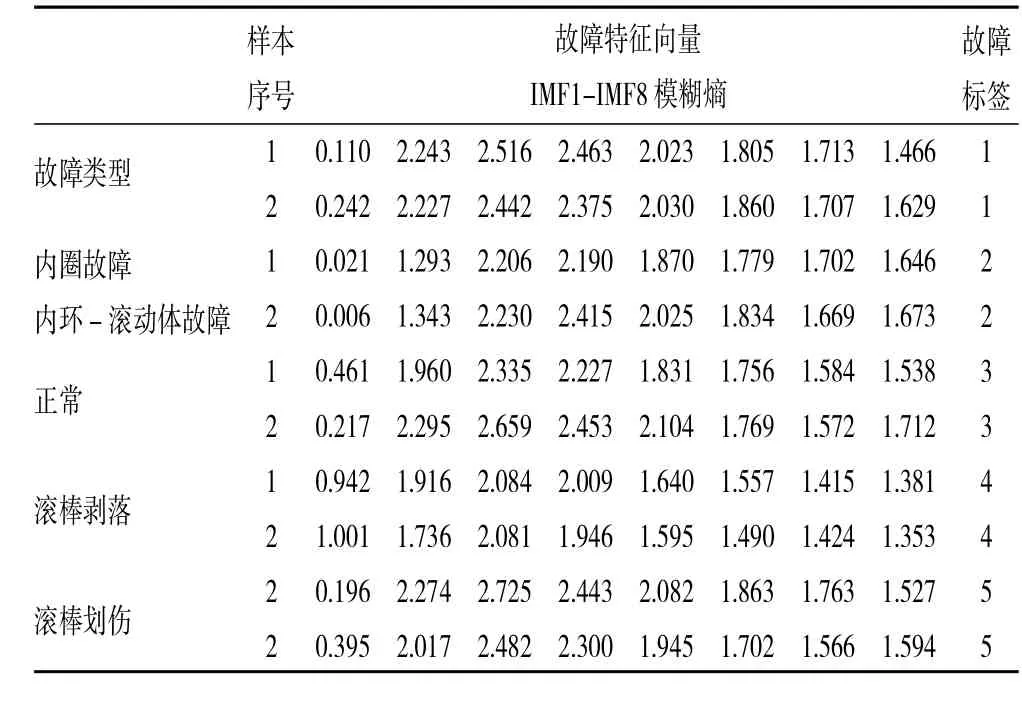
表2 部分EMD模糊熵故障样本

采用所建立的会诊决策模型对160组训练样本进行分类测试，分类结果如图5、6所示。

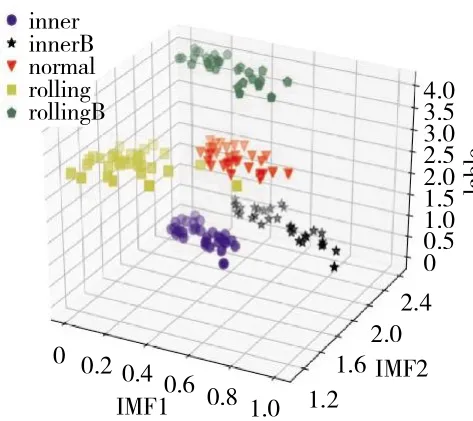
图5 IMF1和IMF2维度的分类结果

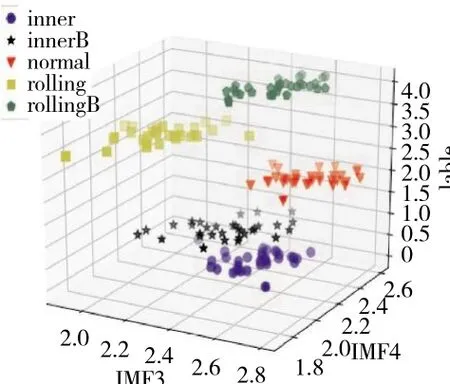
图6 IMF3和IMF4维度的分类结果

从图5、6中可见，样本数据在IMF1-2上的类聚性最优，IMF3-4次之。根据聚类结果可知，会诊模型在对于160组训练样本能够准确分类，分类准确率达到100%。

为了验证模型的泛化能力，采用40组测试样本对所建立的会诊模型进行测试。故障诊断结果如图7所示。

从图中可见，会诊模型的泛化能力较好，最终实现了92.5%的诊断率。其中在图中圆圈标记的3个点为错误分类情况。即错误的将内环故障状态混同于内环和滚动体联合故障状态。这是由于2种故障模式中内环都存在故障，故障样本的EMD模糊熵较为相似，因此出现误分类。而会诊模型在对正常状态、滚棒划伤状态以及滚棒剥落状态下表现良好，均实现了零失误诊断。由此可见，会诊模型在某型航空发动机中介轴承故障诊断中表现出良好的泛化性能。

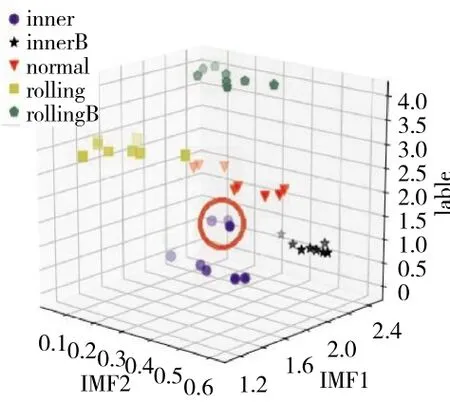
图7 泛化性能测试结果

3.3 模型间的泛化能力比较

为验证会诊模型的决策性能优于单一模型，采用相同的训练集和测试集分别对5种单一模型和会诊模型进行训练并进行泛化能力测试。模型间的故障诊断准确率比较如图8所示。

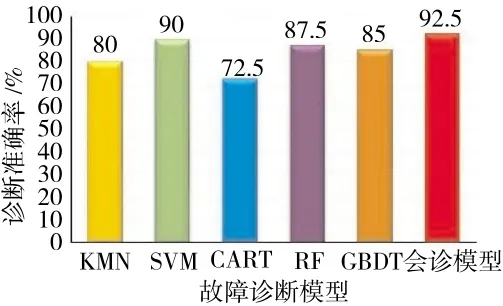
图8 模型泛化能力比较

从图中可见，会诊模型诊断准确率达到92.5%，优于其他基础识别算法，在试验中SVM、RF以及GBDT模型分别以90%、87.5%和85%取得较好的分类结果，而kNN、CART模型诊断准确率则小于80%相对落后。同时，试验验证了本文所选取的基础模型在保持较好泛化能力的同时且存在一定决策能力差别，因而成功地实现了差异化的基础模型选择过程。