某型涡桨发动机吹风流场计算与试验对比

2019-12-13许思琦

航空发动机 2019年5期

孙科，丁旭，王欢，许思琦

（中国飞行试验研究院，西安710089）

0 引言

动力装置及飞行器地面试验是设计定型中的必要环节，侧风试验即为其中1种，侧风试验对风速大小进行了规定。从安全方面考虑，对动力装置及飞行器进行侧风试验考核是十分必要的，如九寨黄龙机场存在热力环流形成的下坡风引起的130毅侧风，重庆江北机场[1]也受到北风为侧风的影响。在国军标及航标中均有相关规定要求地面试验需在一定风速条件下进行。中国民用航空规章第25部[2]中对演示的侧风风速有如下要求：对于陆上飞机和水陆两用飞机，必须制定在干跑道上对起飞和着陆经演示时安全的90毅侧风分量，该分量必须至少是10.29 m/s或0.2VSRO（取大者，但不超过12.86 m/s）。其中1节约为0.51444 m/s,VSRO为飞机在着陆构型下的参考失速速度。文献[3]中对民用飞机大侧风验证试飞方法进行了研究。进行侧风试验时，较大侧风速度气象条件可遇不可求，依赖于自然风一般会耽误试验进度及安排。因此可在专用机场进行侧风试验，如A380飞机曾在冰岛雷克雅未克机场成功完成了大风速情况下的侧风试验。另外国外已有采用涡桨发动机尾流为该类试验提供风场条件的先例。发动机尾流速度较大，如单发不能满足要求，还可以双发同时运行，保证风量风速充足。

由于螺旋桨高速旋转，涡桨发动机尾流十分复杂，航向速度及周向速度都较大。如果使用发动机尾流作为地面试验条件，必须先期了解流场分布规律，进而规划地面试验。因此对装机环境下发动机尾流流场进行数值计算很有必要。文献[4]中自主开发建立了针对螺旋桨、风力机等旋转机械的定常和非定常计算模块；文献[5]针对螺旋桨进行理论设计，并应用于滑流数值模拟研究中；文献[6-12]针对螺旋桨进行数值计算；文献[13]针对预旋系统中的旋转盘腔这种转、静交界面问题进行数值计算；文献[14]中应用S-A湍流模型对绕翼流场进行计算。

本文针对该问题建立实体模型和流体域模型，使用ICEM软件进行网格划分，使用Fluent软件计算。为验证计算模型和计算方法的准确性，对该型发动机尾流流场中关键点风速进行了测量。

1 某型发动机尾流流场计算

1.1 实体模型、流体域模型

采用UG软件进行3维建模，实体模型如图1所示，之后建立流体域计算模型。

计算流体域的静止部分（如图2所示）占据大部分，进口在桨叶旋转平面前20 m处，出口在桨叶平面后45 m处，上方及周向为计算域的出口通风边界，距离发动机轴心20 m。由于工作状态下发动机进口进气，而进气对尾流无影响，在尾流计算时，将发动机进口设置为固体壁面。但是发动机出口有高速气流流出，对尾流场有较大影响。短舱外壁面按照实际条件设置为固体壁面。静止域内边界为飞机机体壁面和转、静交接面。如图2所示计算域中小圆柱范围内为转动域，转动域是以发动机轴心为中心，半径为2.5 m的圆柱。圆周面及左右平面为转、静交接面，桨叶及轮毂面为转动面。转动域与静止域的交接面采用动参考系模型（MRF方法）进行流场信息传递。将这个非定常问题在时间上时均化，以这种定常方法来近似等效。

图1 实体模型

图2 转动域及边界条件

使用ICEM软件对流体域进行网格划分，算例中共划分3355951个网格单元。转静交接面两侧面网格数量基本相当。对螺旋桨表面网格进行了加密，共划分116793个面单元。

1.2 计算方法及边界条件

1.2.1 湍流模型

对纳维斯托克斯方程做时间平均处理，即雷诺平均法（RANS），可以得到湍流基本方程，因此而引入脉动量，如式1所示。

为了使方程组更具有封闭性，必须模化雷诺应力，引入模型使方程组封闭。按照基于Boussinesq的涡黏假设湍流黏性系数法有

式中：xi、xj为 i、j方向的位置坐标；ui、uj为 i、j方向速度的瞬时值；ui、uj为i、j方向速度的时均值；ui'、uj'为i、j方向速度的脉动值；p为压力的时均值；μt为涡黏系数；ui为时均速度；δij为 Kronecker符号（当 i=j时，δij=1；当 i屹j时，δij=0）；k 为湍流动能

涡黏系数可由湍流模型来确定，本文选择S-A模型[14]，其对计算有很强的鲁棒性，流场湍流涡黏度场连续，并且占用的CPU和内存更少。S-A模型中的涡黏系数为

式中：v'为湍流的脉动黏度；fv1为湍流的脉动黏度v'与分子黏度v比值的函数。

1.2.2 物性参数及边界条件

材料物性中空气密度选择ideal-gas，流体的动力黏度μ由流体本身固有物理性质所决定，压力变化对μ的影响较小，压力小于10个标准大气压，其影响可以忽略不计。但是温度对μ的影响较大，气体的动力黏度随温度的升高会增大，本文计算中会考虑尾喷管出口的高温气体，因而选择sutherland公式进行计算。同时在计算中对能量方程也进行求解

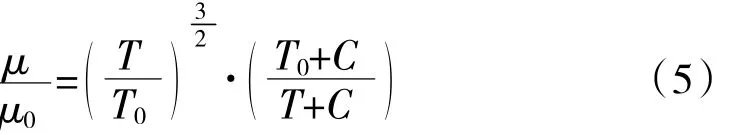
式中：对于空气，C=111；空气在T0=273.15 K时的动力黏度 μ0=1.17×10-5。

空气密度选择ideal-gas，即由理想气体状态方程[15]计算得到

式中：p为静压；ρ为空气密度；Rg为气体常数；T为气体静温。

进口边界条件为压力进口，计算开始时，此压力设置为稍大于大气压力，待计算形成稳定的流场后，将此压力改为大气压力。出口边界条件为压力出口，周向为出口通风。桨叶表面设置为旋转面，桨叶周围设置为转动域。

1.2.3 转、静交接面法

转、静交接面法（MRF方法）是针对旋转机械问题的1种定常处理方法，因转动壁面对气流作功，且一般该类问题为非定常问题，在Fluent中可采用动网格方法对其进行模拟。但是这种方法计算量大、耗时长，采用MRF方法节省计算资源，静止域与转动域间采用转、静交接面进行流场信息交换。

由（x，r，φ）组成的静止圆柱坐标系如图3所示，空间中1点的速度为（ux，ur，uφ），旋转坐标系如图4所示，其以ω的角速度绕x轴旋转，旋转坐标系下相同点处的速度为（ux'，ur'，uφ'）。该点处静止坐标系下的速度和转动坐标系下的速度关系见式（7）。x方向及r方向速度相等，只有φ方向速度相差φr。

图3 静止坐标系

图4 转动坐标系

由于桨叶面以ω进行旋转，在转动坐标系中相对静止，气流以（ux'，ur'，uφ'）的速度进行运动，该问题化简为气流冲击静止壁面，便于求解。

2 试验简介

某型飞机共安装4个涡轮螺旋桨发动机，发动机后较大范围内可以保持较大的流速，比较适合做地面试验的风源。在进行飞机发动机地面试验时，在发动机正后方布置测量耙，进行流场流速测量试验。单独运行单发或双发，发动机起动前将测量耙安装调试到位。由于螺旋桨旋转平面距离尾翼最后端有一定距离，考虑到移动试车台会占一定空间，并且为安全起见，应使试验台与飞机间保持一定距离，因而在距离双发螺旋桨旋转平面37.2 m处，布置测点竖直分布的测量耙。

飞机上方视角测量耙位置分布如图5所示，飞机前方视角测量耙测点位置分布如图6所示。在距离地面 1.00、1.83、2.66、3.50、4.32、6.00 m 高度上分别布置皮托管。皮托管的总静压测管接入至差压表中，差压表信号接入至数采系统，数采系统与计算机间通过网线连接。

发动机螺旋桨尾流空气流速在低马赫数范围内，可由总静压差计算得到

图5 测量耙位置分布

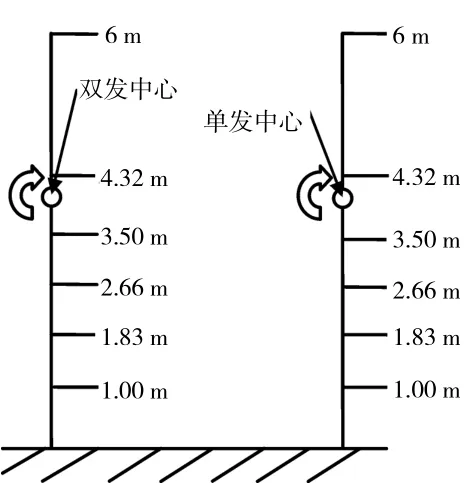
图6 测量耙位置分布

式中：p*为气流总压，v为速度。

3 试验结果与计算结果的对比

3.1 尾喷管气流对计算的影响

针对发动机地面起飞状态，对是否考虑尾喷管出口气流的2种情况进行了计算，2种不同条件下的速度计算结果如图7所示。图中横轴为发动机轴向方向上的坐标，纵轴为高度方向上的坐标。不考虑尾喷管气流的计算中将尾喷管出口设置为壁面。考虑尾喷管气流的计算中将尾喷管出口平面设置为该计算模型的1个入口，截面参数从参考资料中地面台架试验结果图读取。

图7 发动机中心截面速度

本文中使用无量纲速度ux表示气流速度大小，为x方向真实速度与流场中所选1点参考速度ux，0的比值，无量纲速度定义为

在图7中以空间中真实速度较大的1点作为参考速度ux，0，可见，是否考虑尾喷气流对尾流速度分布的影响较大。

是否考虑尾喷管气流的2种情况下，不同点速度分布情况对比，试验中对h=1等几点的x方向速度进行测量，因此计算结果也将这几个点的数据进行统计。其中以2种条件下，所统计6点速度最大的1点作为参考速度ux，0。是否考虑尾喷管气流结果对比见表1。由表中可见，是否考虑尾喷管气流，对较高点处的计算结果影响不大，如h=6 m处2种计算结果无量纲速度差0.04。但高度较低处的气流流速差别较大。这是由于尾喷管有向下倾斜的角度，喷出气流向下稍有偏转，且气流受到机翼的作用，会产生下洗流效应，因此随着高度的降低，2种计算条件下气流速度差别越来越大，如图8所示。速度差在h=1.83 m处最大，不考虑尾喷管气流时，该点x方向无量纲速度为0.5，当考虑尾喷管气流时，x方向无量纲速度为0.97。因此必须考虑尾喷管气流才能准确计算尾流场风速。

表1 是否考虑尾喷管气流结果对比

3.2 单发结果对比

对该架飞机单发位置的发动机，针对地面起飞状态进行计算。该工况下不同高度的气流速度计算与试验结果的对比如图9所示并见表2。其中以统计计算及试验结果中，速度最大的1点作为参考速度ux，0。由于螺旋桨旋转是非定常问题，试验测量得到的结果随着时间变化不断波动，数值模拟中采用定常方法求解。因而对试验结果的处理方法是在1个时间段内求取平均值，与计算结果进行对比。在1 m高处的无量纲速度偏差最小为0.06，在4.32 m高处的无量纲速度偏差最大为0.17。计算结果与试验结果间存在一定的偏差，这是因为计算模型不一定完全准确，试验测量存在一定的误差，并且在试验环境下受到自然风的影响，对螺旋桨尾流产生干扰。