弹性环式挤压油膜阻尼器流固耦合计算

2019-12-13江志敏高雄兵

航空发动机 2019年5期

江志敏，高雄兵，张鹏

（中国航发四川燃气涡轮研究院，成都610500）

0 引言

现代航空发动机除了追求高性能和高推重比外，还要求发动机有更轻的质量和更紧凑的结构布局，这些特点会使发动机在工作转速范围内存在临界转速。所以高性能和高可靠性的燃气涡轮发动机的研制要求转子系统具有优良的阻尼减振器，以减小转子系统接近临界转速和通过临界转速时的振动。这是整机动力学设计的关键技术之一。

近年来，国内许多学者对弹性环式挤压油膜阻尼器（ERSFD）做了一些探索性研究。周明等[1-3]对ERSFD的减振机理进行了初步探索，建立了油膜压力控制方程，分析了油膜力特性；周松江、赵行明等[4]对弹性环挤压油膜系统进行了试验研究；洪杰等[5]以燃气涡轮发动机用ERSFD为对象，基于有限元挤压油膜理论对ERSFD的弹性环支承刚度、油膜压力场分布和油膜阻尼等特性进行了研究；曹磊等[6-7]推导了ERSFD的雷诺方程，通过对ERSFD数学物理模型的求解，研究了ERSFD油膜力特性。这些研究都是基于流体力学或试验的方法对ERSFD特性进行研究。

本文引入流固耦合的计算方法，考虑弹性环变形和滑油流场的相互作用，建立3维有限元流体和结构模型来耦合求解ERSFD滑油的流动情况，获得油膜压力分布特性以及弹性环在复合载荷作用下的计算结果，为了解ERSFD的减振机理以及进行结构设计提供1种新的设计思路。

1 流固耦合ERSFD模型

1.1 ERSFD结构

弹性环式挤压油膜阻尼器在传统挤压油膜阻尼器的基础上增加了具有定心弹性支承作用的弹性环，弹性环内、外凸台分别与轴承外环和限幅器接触面配合，把整个油腔沿径向分隔成内、外2层油腔，弹性环凸台又分别把每层油腔沿周向分隔成多个小油腔，油腔之间通过弹性环上的阻尼孔相连通[8-15]，具体结构如图1所示。本文以某ERSFD算例对流固耦合特性进行计算分析。

图1 ERSFD结构

1.2 ERSFD流固耦合模型

ERSFD的流固耦合模型关系如图2所示。从图中可见，弹性环在油腔里被滑油包围，其表面均是流固耦合界面。在流固耦合模型中，虽然滑油被弹性环分割成若干小油腔，但是由于阻尼孔和凸台上间隙的存在，使得流体模型为1个联通的流域。

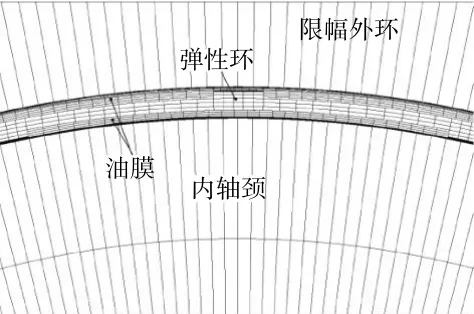
图2 ERSFD耦合关系

处理流固耦合模型时，对结构和流体分开建立模型，二者相互独立且允许一定的公差存在，通过流固耦合界面相互联系，并传递作用力。在处理模型时，一些细节的处理决定了计算边界条件是否成立。其一，结构建模及边界处理。在ERSFD的流固耦合计算模型中，需考虑弹性环与内轴径、限幅外环之间的装配关系，并且定义接触，给定1个合适的接触容差范围，模拟弹性环受到不平衡力挤压作用时与内、外刚性结构的真实接触关系。文中弹性环内、外实际装配间隙均设置为0.06 mm。其二，流体模型与流固耦合边界处理。弹性环与内轴径、限幅外环之间的所有空隙均为ERSFD中流体的部分，包括凸台上方的0.06 mm装配间隙。在建立流固耦合边界时，需要在所有流体和结构产生交互的界面上建立流固耦合方程。所以，在ERSFD实际工作过程中，流体的流动通道不止阻尼孔，还包括凸台上方的装配间隙，在不平衡力作用下，结构之间的接触导致流体的流动变得复杂。ERSFD的流体和结构有限元模型分别如图3、4所示。

图3 流体部分有限元模型

图4 结构部分有限元模型

1.3 流固耦合计算条件

假设激励为内轴颈随时间逐步增大到最大偏心距后做稳态公转运动。计算流体和结构模型中的时间积分必须是相容的，计算均收敛于同一时间载荷步，内轴颈偏心距随时刻的初始输入激励如图5所示。内轴颈公转2圈，转速为10000 r/min，第1圈其偏心距幅值由0逐步增大到最大值。

图5 ERSFD响应计算输入激励

2 流固耦合特性计算结果

2.1 弹性环计算结果

通过流固耦合方法计算得到在内轴颈公转及滑油压力共同作用下弹性环的变形结果及振动应力的分布情况。

在传统弹性环强度计算中，无法考虑到ERSFD中流场压力的作用，只能得到弹性环受内轴承偏心载荷下的静强度计算结果。在ERSFD实际工作过程中，油膜压力会导致刚性较弱的弹性环发生变形。如算例中，不平衡力作用于正上方位置时，弹性环的变形结果对比如图6、7所示。从图中可见，考虑流体压力作用后弹性环的变形要比单一机械载荷作用复杂很多，其变形量也要比单一机械载荷作用时的大。由弹性环的变形结果对比可知，在受到机械挤压力作用的位置，采用流固耦合方法和传统固体力学方法计算得到的变形分布及变形量值基本相当。采用流固耦合方法计算考虑了油膜对弹性元件的作用，图中在油膜压力较大的位置，弹性环受到挤压而变形。

图6 流固耦合计算得到的弹性环变形

图7 机械载荷作用下的弹性环变形

弹性环受到相同强迫位移作用下的等效应力如图8、9所示。从图中可见，流固耦合计算得到的等效应力大于仅考虑机械载荷得到的计算结果，且能考虑到流体对阻尼孔的冲压作用，其最大等效应力的位置出现在阻尼孔附近。通过流固耦合分析，ERSFD中弹性环的高周疲劳源很可能出现在阻尼孔周边。

图8 流固耦合计算弹性环等效应力分布

图9 仅受机械载荷弹性环等效应力分布

为了更好的理解弹性环的变形及应力分布特征，对ERSFD的流体部分的压力特性及流动特性进行分析。

2.2 压力分布

通过流固耦合计算得到了内轴颈以稳定的偏心率运动到相位差为90°的4个位置时油膜压力的分布。4个位置与进油口的位置关系如图10所示；假设转子的振动幅值达到0.5偏心率时，轴颈分别挤压与进油口位置成90°、180°、270°、360°时油膜沿圆周的分布如图 11 所示。

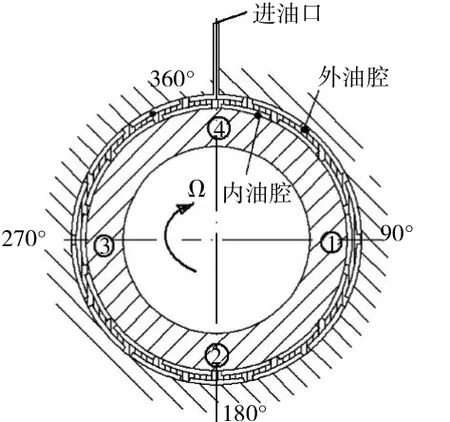
图10 读取油膜压力位置关系

在ERSFD内轴颈偏心力作用下，油腔内的滑油被挤压后，滑油通过阻尼孔和间隙向压力更小的油腔流动。由于弹性环本身刚度较弱，在内轴颈偏心挤压作用下也会变形，由此可知ERSFD的滑油流场受到内轴颈偏心挤压及弹性环变形的共同影响。

图11 轴颈挤压与进油口成不同角度时油膜压力沿圆周分布

通过流固耦合方法计算得到油膜压力的特点如下：

（1）油膜压力分布总趋势与SFD的相似，但呈阶梯式分布；

（2）相邻油腔之间的压力梯度差主要来自于阻尼孔处的节流作用；

（3）由于进油压力的设置，轴颈运动在不同偏心角时，油膜压力分布特点各不相同；

（4）单个油腔内由于周向黏性阻尼作用也会产生一定的压力梯度。

2.3 滑油速度计算结果

通过流固耦合计算得到ERSFD中滑油的速度矢量分布如图12所示；油膜阻尼孔截面局部的流体矢量如图13所示；ERSFD轴向剖面内、外油腔压力分布及压力差如图14所示，滑油流动情况如图15所示。

从图12中可见，ERSFD油膜阻尼的滑油流动速度较大的部位有2处：凸台与限幅外环、内轴颈之间间隙处的周向流动和阻尼孔处的径向流动。

图12 ERSFD阻尼孔截面滑油速度矢量

图13 ERSFD6点钟位置流体矢量

图14 ERSFD轴向截面滑油压力分布

图15 滑油流动

通过对ERSFD速度矢量以及阻尼孔处滑油流动特点的分析可知ERSFD阻尼孔在减振中的作用：内轴颈公转压迫滑油，滑油进入阻尼孔和凸台间隙后，由于惯性流束将继续收缩直至缩颈的最小截面流速增大，然后又逐渐扩大，直至碰撞到限幅外环或内轴颈的表面。在缩颈附近的流束与阻尼孔壁之间以及滑油流出阻尼孔后的拐角与流束之间都有1个充满小漩涡的低压区。漩涡靠主流束带动着旋转，主流束把能量传递给漩涡，漩涡又把得到的能量耗散在旋转运动中，变成热而散逸，形成明显的节流损失，把振动能量转化为热能。