分数阶Rosenau-Haynam方程的残差幂级数解法

张建科, 王 源，魏至柔

(1.西安邮电大学 理学院， 陕西 西安 710121； 2.南京理工大学 化工学院， 江苏 南京 210094)

分数阶微分方程在流体力学、黏弹性力学、生物数学、分数控制系统以及物理学等领域得到了广泛应用，但大多数问题很难得到解析解。目前的近似解析方法包括：同伦扰动法(HPM)[1]、李群方法[2]、变分迭代法(VIM)[3]、同伦变换[4]、同伦渐近法[5]、G′/G展开法[6]、多项式最小二乘法[7]、有限差分法[8]等。本文将采用残差幂级数法(RPSM)[9]求分数阶Rosenau-Haynam方程的近似解析解，这是一种基于分数阶幂级数展开的分析方法，已被成功应用于多种分数阶微分方程。

分数阶Rosenau-Haynam方程如下：

(1)

初始条件为

(2)

其中u=u(x,t)，α(0<α<1)是微分阶数参数，t是时间，x是空间坐标。

当α=1时，方程精确解：

(3)

1 残差幂级数法

定义1[10-11]给定连续函数f(t),设n是大于等于α(α≥0)的最小整数，则Caputo分数阶导数定义为

定理1[12]通过Caputo分数阶导数，可得：

定义2[13-14]当n-1<α≤n，t≥t0时，幂级数展开式为

称之为在t=t0时的分数阶幂级数，其中cm是一个常数，为幂级数的系数。

定理2[13]设f表示t=t0时分数阶幂级数的展开形式，则f(t)为

若Dmαf(t)∈(t0,t0+R),m=0,1,2,…，则分数阶幂级数展开式的系数cm为

其中R是收敛半径。

定义3[14]当n-1<α≤n，t≥t0时，幂级数展开式为

称之为t=t0时的广义分数阶幂级数。其中t是变量，fm是关于x的函数。

定理3[13-14]假设u(x,t)在t=t0时的广义分数阶幂级数展开式为

(4)

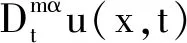
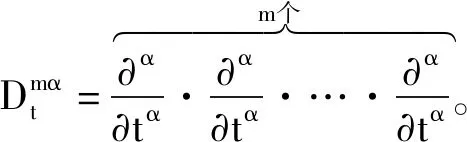
则分数阶幂级数展开式可被写为

定义u(x,t)的幂级数展开式的前i+1项和ui(x,t)为

(5)

该展开式为式(1)的近似解。

如果t=0,u(x,0)=f0(x),基于式(1)的基础上定义第i个残差函数为

(6)

为了得到fn(x),令：

2 残差幂级数法计算分数阶Rosenau-Haynam方程

本文中Rosenau-Haynam方程的初始条件是式(2)，α=1时精确解是式(3)，第i个残差函数Resi(x,t)如式(6)。

第一步，令i=1，则分数阶Rosenau-Haynam方程为

将i=1代入式(5)得：

则：

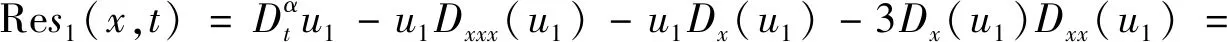
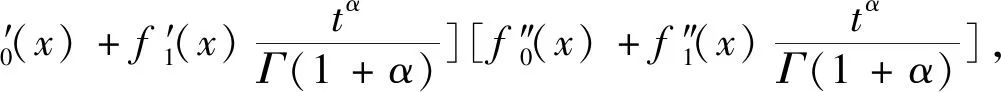
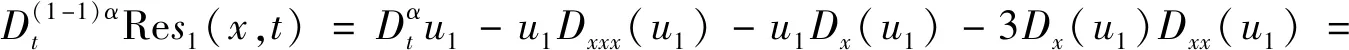
第二步，令t=0,则：

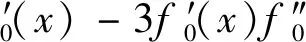
且：

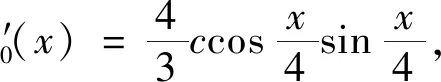
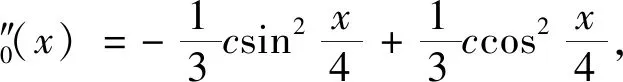
则：

第三步，依照上法：

令：

因此,分数阶Rosenau-Haynam方程的三项近似解为

3 结果分析

使用残差幂级数法计算了分数阶Rosenau-Haynam方程的近似解析解。在表1—表3中对x和t分别取与文献[1]相同的值以便与之比较。

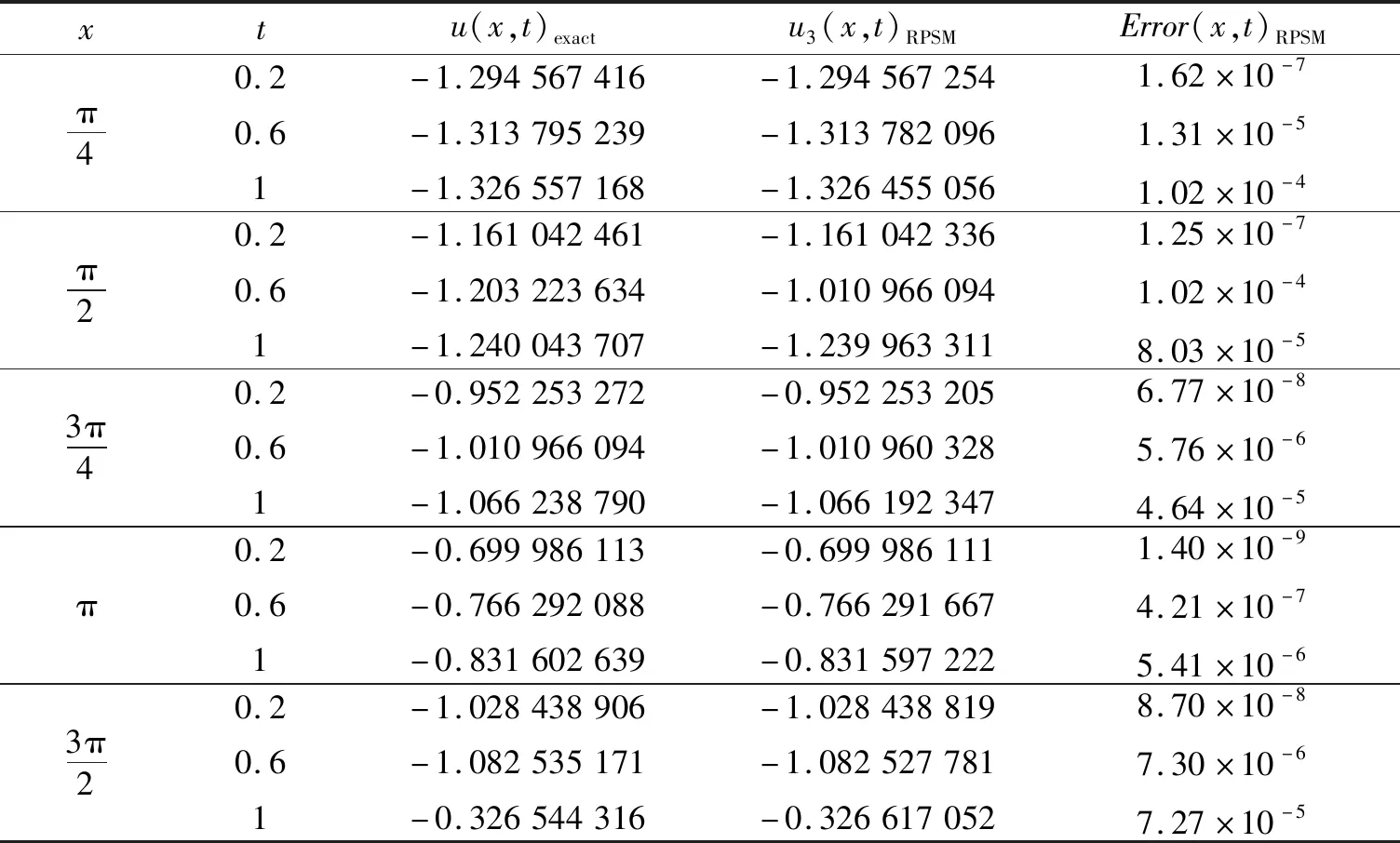
表1 当α=1时残差幂级数法的绝对误差

表1中，在相同的x、t之下令α=1、c=0.5，求方程的精确解和近似解，绝对误差如表中所示。可以看出在x不变的条件下t越大，误差越大；在t不变的条件下x越大，误差越小。

表2 残差幂级数法与变分迭代法绝对误差对比

表2中，在相同的x、t下令α=1、c=0.5，在展开相同的项数条件下，将残差幂级数法求得的误差与文献[1]中给出的变分迭代法三项近似解的表达式求得的误差进行了比较，由表中看出残差幂级数法求得的误差更小、精度更高。

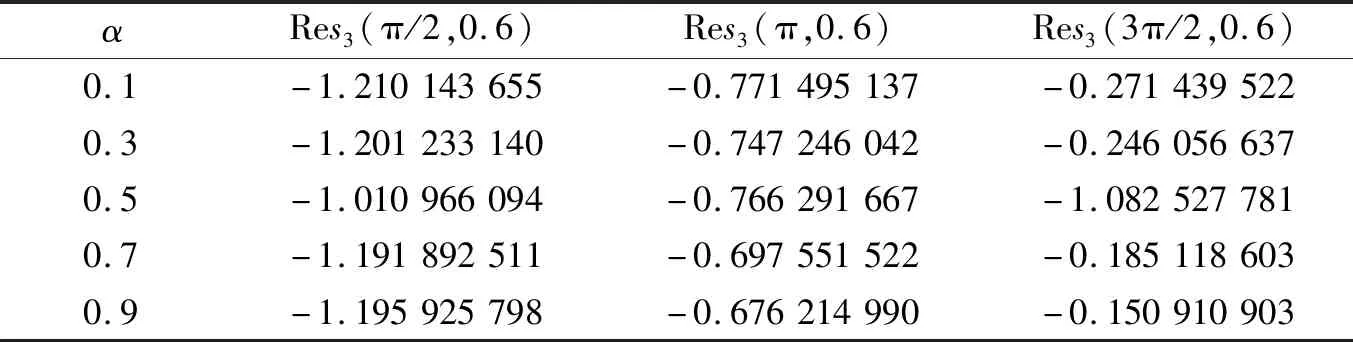
表3 不同α与x对三项残差函数值的影响

表3中，得到三项残差函数Res3(x,t)的值。如果t和α的值是固定的，则Res3(x,t)的值随着x的增加而增大。当Res3(x,t)的值接近0时，近似解接近精确解。

4 结 论

利用残差幂级数法求解分数阶Rosenau-Haynam方程的解析解，并通过表的方式展现出解的精度，在相同条件下与变分迭代法(VIM)做了比较。结果表明残差幂级数法所得的解更接近精确解，是求解分数阶Rosenau-Haynam方程近似解析解的一种有效方法。