含两个空间分数阶导数热方程的非标准有限差分解法
2019-12-11刘子婷
刘子婷
(广东工业大学 应用数学学院, 广东 广州 510520)
分数阶导数由于具有非局部性,可以有效地描述具有记忆和遗传特征的自然过程。近几十年来,分数阶偏微分方程在控制工程、物理力学、生物学和计算机科学等学科中得到了广泛的应用[1-5]。尤其空间分数阶偏微分方程常被用来模拟超扩散,是因为其中粒子羽流的扩散速度比经典布朗运动模型预测的要快。Chen等[6]考虑了具有分数阶扩散和整数阶平流项的空间分数偏微分方程,并且通过有效地结合Legendre spectral和Crank-Nicolson差分法得到了目标方程完全离散的数值解。Zhou等[7]建立了Riesz空间分数阶偏微分方程的Crank-Nicolson有限差分格式,并且讨论了该格式的稳定性和收敛性,其中理论分析和数值实验的结果表明,该方法是有效可行的。Ali等[8]利用改进的扩展tanh方法,并使用数学软件Mathematica对两类时空分数阶偏微分方程进行处理,给出了这两类方程的新结构。Mickens[9]提出了求解微分方程的数值方法:非标准有限差分法,在某种意义上,该方法克服了经典有限差分法的一些不足。Agarwal等[10]结合非标准有限差分法和切比雪夫配置法,得到了一类空间分数扩散方程的非标准差分格式,通过数值模拟,发现该方法所得到的数值结果不仅优于以前的方法,而且大大提高了收敛精度,进而验证了该方法的有效性和准确性。
在本文中,我们考虑以下空间分数阶热方程:
(1)
初始条件为
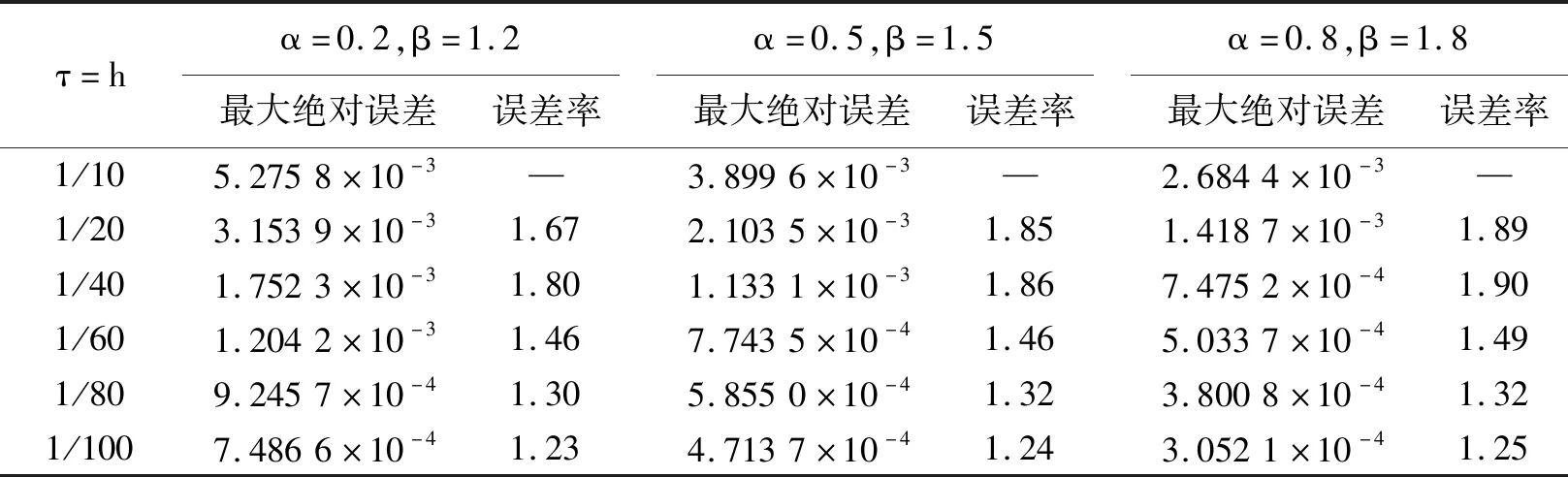
u(x,0)=s(x),0 (2) 边界条件为 u(0,t)=u(L,t)=0,0 (3) 因为热方程中涉及到两个分数阶导数,这会使得数值计算有一定的困难,需借助Grünwald-Letnikov公式和带位移的Grünwald-Letnikov公式来离散两个空间分数阶导数,从而降低数值计算的难度。由Agarwal和El-Sayed[10]的研究受到启发,本文将结合非标准有限差分法和Crank-Nicolson差分法得到含两个空间分数阶导数热方程的非标准有限差分格式。 f(xj,tn),1≤j≤m-1,n≥1, (4) u(xj,0)=s(xj),1≤j≤m-1, (5) u(0,tn)=u(m,tn)=0,n≥1, (6) 将非标准有限差分法和Crank-Nicolson差分法结合起来,得到式(4)的非标准有限差分格式,如下所示: (7) (8) 将式(8)改写成矩阵形式 (I+A)Un+1=(I-A)Un+φ1(τ)Fn+1/2, 其中 I是一个(m-1)×(m-1)的单位矩阵,A=(ajn)是一个(m-1)×(m-1)的系数矩阵,其中 定理2.1 当0<α<1,1<β<2时,非标准有限差分格式(4)是无条件von Neumann稳定的。 (9) 定义 (10) 其中i是虚数单位,q是空间波数。将式(10)代入式(9)中得到 则 (11) 令 (12) 证明首先计算局部截断误差R的阶数,R的表达式为 其中 (13) (14) u(xj-(k-1)h,tn)]+o(h), (15) 将式(13)—(15)代入R的表达式中得到 u(xj-(k-1)h,tn)]-f(xj,tn+1/2)+o(τ2+h), 所以局部截断误差R的阶数为o(τ2+h)。 (16) 将式(16)写成矩阵形式为 (I+A)En+1=(I-A)En+φ1(τ)R, (17) 令K=(I+A)-1(I-A),P=(I+A)-1,式(17)可改为 En+1=KEn+PY, (18) 考虑下述问题 f(xj,tn),0 (19) u(x,0)=s(x),0 (20) u(0,t)=u(1,t)=0,0 (21) 1)令φ1(τ)=τ,φ2(h)=h。图1所示的是当0 (a)解析解 (b)数值解图1 问题(19)—(21)的解(0 τ=hα=0.2,β=1.2最大绝对误差误差率α=0.5,β=1.5最大绝对误差误差率α=0.8,β=1.8最大绝对误差误差率1/107.2899×10-3—5.6731×10-3—4.2503×10-3—1/204.0691×10-31.792.9616×10-31.922.2225×10-31.911/402.1501×10-31.891.5545×10-31.911.1449×10-31.941/601.4501×10-31.481.0534×10-31.487.6952×10-41.491/801.1066×10-31.317.9596×10-41.325.7923×10-41.331/1009.1476×10-41.216.3892×10-41.254.6480×10-41.25 2)改变时间分母函数,空间分母函数保持不变,即φ1(τ)=1-e-τ,φ2(h)=h。比较表1和表2中的数据,可以得出最大绝对误差在减小,这表明改变时间分母函数可以提高精度。 表2 问题(19)—(21)的最大绝对误差值以及误差率(φ1(τ)=1-e-τ,φ2(h)=h,T=1) 3)在上一个实验的基础上继续改变空间分母函数,即φ1(τ)=1-e-τ,φ2(h)=eh-1。比较表2和表3的数据可以得出最大绝对误差在继续减小,这表明同时改变时间和空间分母函数会更好地提高精度。 表3 问题(19)—(21)的最大绝对误差值以及误差率(φ1(τ)=1-e-τ,φ2(h)=eh-1,T=1) 在本文中,我们使用了具有时间和空间步长的分母函数来构造空间分数阶热方程的非标准有限差分格式,并证明了该差分格式的稳定性和收敛性。在数值算例中,通过构造不同的分母函数来减小最大误差,为理论证明提供了依据。结果表明,非标准有限差分法用于求解含两个空间分数阶导数的热方程是有效且可行的。
1 非标准有限差分格式

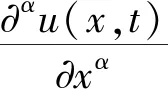

2 稳定性与收敛性分析






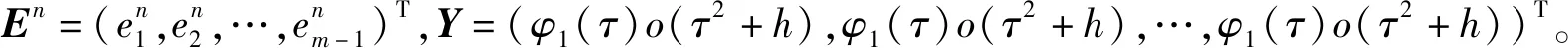

3 数值算例




4 总 结
