不同材料储能飞轮应力特性分析及研究

苏 芳，王晨升，赵海燕，雷美荣

（山西大同大学机电工程学院，山西 大同 037003）

作为一种新型清洁电能储备技术，飞轮储能具有储能密度大、高效无污染、充电快、使用寿命长等优点，能够稳定频率和电压，减小可再生能源的波动性，因此得到越来越多地关注，广泛应用于供电、交通、航空航天和军工等领域[1-2]。在工作工程中，飞轮储能系统通过飞轮高速旋转实现能量存储，转速越高，其储能容量越大。但是，飞轮的转速与其材料、结构等因素紧密相关，因此，为提高储能能力，需开展广泛地飞轮材料及结构等相关研究[3-5]。

目前，行业内已有诸多学者对储能飞轮相关特性进行了分析研究。李成等[6]结合复合材料和预应力的特点，建立了基于各向异性对称结构的计算模型，对飞轮在特定转速情况下不同的位置对径向应力、环向应力和径向位移的影响进行了探讨。姚华[7]基于商用有限元软件搭建了储能飞轮应力分析模型，利用仿真分析和数值计算方法相结合，对最大过盈量装配时飞轮系统的接触应力与旋转状态下的离心应力进行了分析计算，以此为基础完成了飞轮强度校核。芦晨祥等[8]基于平面应力状态假设，构建了多环混合复合材料的飞轮应力模型，利用数值解析法分析了环间环数、模量比、环厚、环间过盈量等因素对转子静止和高速旋转时应力分布的影响。秦勇等[9]利用平面应力状态假设, 给出计算多环环间混杂复合材料飞轮在离心力作用下应力和初始极限转速的方法。贾红雨等[10]基于3 种常用的铝合金、钛合金和40Cr 合金材料，建立了飞轮转子模型，研究了不同材料的轮毂对各种条件下飞轮应力的影响。

本文以储能飞轮转子为研究对象，基于Workbench，以飞轮径向应力和环向应力为表征，对不同条件下的储能飞轮应力特性及不同飞轮材料的应力变化规律进行了对比分析研究，为储能飞轮的结构设计及优化提供参考。

1 有限元模型的建立

飞轮本体是飞轮储能系统中的核心部件，飞轮上方安装有轴向电磁轴承，下方为可逆电机，可逆电机输出轴需伸入到飞轮内部，同时，考虑飞轮安装等问题，飞轮通常情况下设计为伞状结构。

Workbench则是专门为重新组合这些组件而设计的专用平台，提供了一个加载和管理API的基本框架。本研究采基于商用CAD建模软件完成飞轮的整体建模，然后导入到ANSYS Workbench中进行应力分析，在engineering data选项中赋予飞轮对应的材料系数（弹性模量、密度、泊松比），飞轮的初始材料为7075铝合金，其弹性模量为7.2e10 Pa，密度为2830 kg/m3，泊松比为0.330。结构参数为：外径380 mm，轴径56 mm，厚度220 mm，腹板厚100 mm，腹板孔直径82 mm，轮缘厚度60 mm，轮缘的线速度99.43～298.3 m/s。

为得到较高的分析精度，选用SOLID186 单元类型，并采用自由网格划分模式，设置Relevance参数为 100，Relevance Center 为 Medium。划分网格后得出来的节点数为265272 个，单元数为163599 个。划分网格后的转子部件如图1 所示。

在Static Structural 选项卡中添加Cylindrical Support 约束和Rotational Velocity 载荷，应用约束和载荷后的飞轮有限元模型如图2 所示。

2 飞轮转子应力分析

实践工程应用中，为保证飞轮能够稳定的工作，对于飞轮储能系统的设计，在已经确定飞轮材料及最大工作转速的情况下，其结构设计、加工工艺则十分关键。在考虑到材料特性的基础上，应充分考虑飞轮内部应力分布情况，以保证飞轮在工作过程中具有稳定的动态特性。储能系统工作过程中，离心力是高速旋转飞轮转子的主要受力，为分析研究方便，可将其分解为径向应力和环向应力。为方便分析，假设材料各项同性，据弹塑性力学理论，等厚空心飞轮半径处的径向应力和环向应力分别为

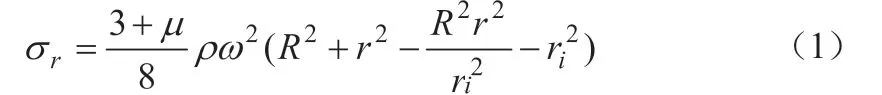
图1 网格划分Fig.1 Meshing

图2 约束和载荷施加Fig.2 Constraints and loads

式中，ρ 为材料密度，kg/m3；ω 为飞轮角速度，r/s；R 为飞轮外径，m；μ 为材料泊松比；r 为飞轮内径，m。

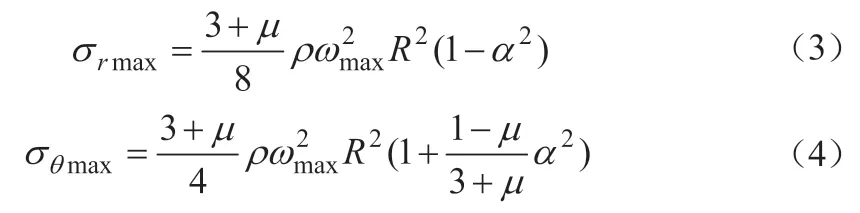
式中，α 为飞轮内外半径比。

在离心力的作用下，飞轮的径向应力σr和环向应力σθ都是大于0 的，同时根据工程设计的Tresca 屈服准则，有

式中，[σ]为飞轮材料的许用应力。

为了分析不同条件下的应力变化规律，设置不同的转速。首先选定5000 r/min，施加载荷进行分析，结果如图3 和图4 所示，飞轮最大径向应力出现在内壁，向外逐渐减小，最大值为27.047 MPa；最大环向应力出现在飞轮轮缘与轮盘交汇处，最大值为13.623 MPa。

以7075 铝合金为例，选取转速分别为5000 r/min、8000 r/min、12000 r/min 和15000 r/min，研究其径向应力和环向应力的变化趋势，如图5 和图6 所示。

对于径向应力，由图5 可见，飞轮的最大径向应力出现在半径35.625 mm 处。由4 种不同转速的应力情况可见，伴随着飞轮转速的增大，其径向应力值也不断增大，在转速15000 r/min 时，出现的最大应力为243.42 MPa。同时，随着转速的增大，径向应力在半径范围内的变化加快，转速为15000 r/min 的阶梯最大，由此可见转速对飞轮边缘应力的分布影响较小，变化较大的地方主要半径范围内的内侧。由图6 可见，对于环向应力，飞轮最大环向应力出现在半径142.5 mm 处，且转速与环向应力正相关，在转速15000 r/min 时，出现的最大应力为122.61 MPa。值得注意的是，环向应力在半径范围内部分单调分布，此情况与飞轮结构相关，因此在结构设计和优化过程中应特别注意。

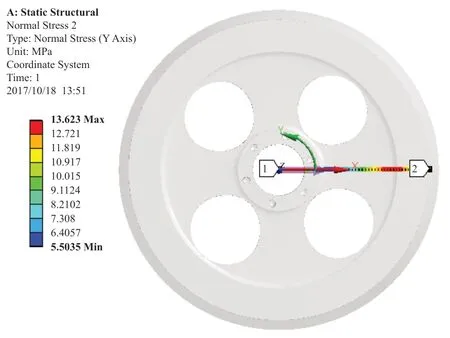
图4 飞轮环向应力云图Fig.4 Ring stress diagram of flywheel

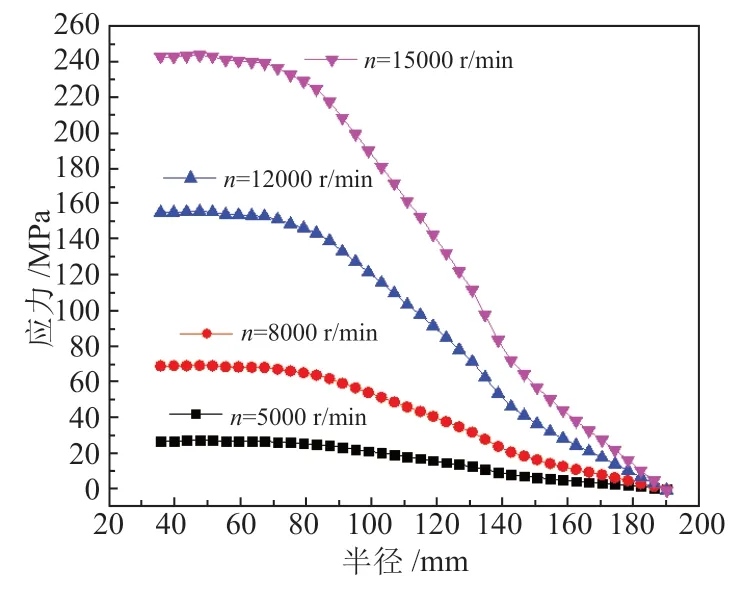
图5 7075 铝合金飞轮不同速度下的径向应力Fig.5 Radial stress of aluminum alloy (7075) flywheel at different speeds

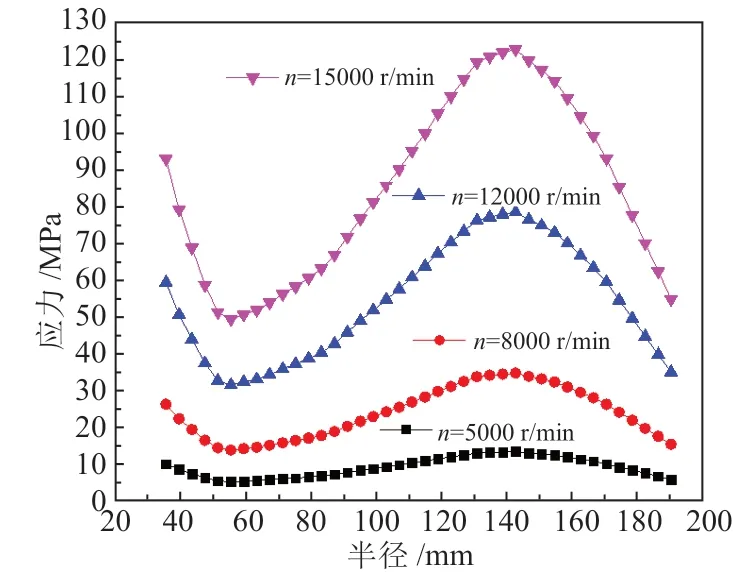
图6 7075 铝合金飞轮不同速度下的环向应力Fig.6 Ring stress of aluminum (7075) alloy flywheel at different speeds

3 不同飞轮材料应力的变化规律

为了深入研究飞轮的应力变化规律，其中飞轮的结构不变，再分别建立了42CrMo，马氏体实效钢和钛合金飞轮的计算模型，材料系数如表1 所示。

采用与上文同样的方法，求得42CrMo 飞轮的径向和环向应力变化趋势，如图7 和图8 所示。

对于径向应力，由图7 可见，42CrMo 飞轮在半径35.625 mm 处出现最大径向应力，且随着转速增加，径向应力值增大，当转速为15000 r/min时，最大应力值为671.75 MPa。由图8 可见，飞轮最大环向应力出现在半径142.5 mm 处，当转速为15000 r/min 时，最大应力为333.63 MPa，环向应力在半径范围内并非单调分布，两种应力都随转速增大而明显增大。

表1 四种材料参数详情Table 1 The parameters of four kinds of material

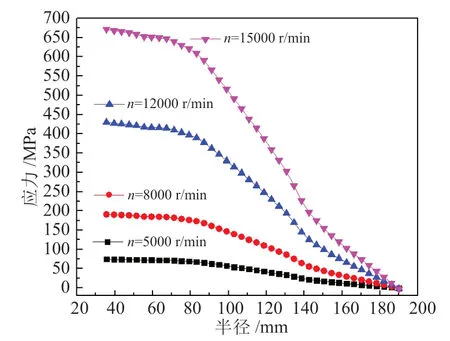
图7 42CrMo 飞轮不同速度下的径向应力Fig.7 Radial stress of 42CrMo flywheel at different speeds

图8 42CrMo 飞轮不同速度下的环向应力Fig.8 Ring stress of 42CrMo flywheel at different speeds

求得马氏体实效钢飞轮径向和环向应力变化趋势如图9 和图10 所示。

对于径向应力，由图9 可见，马氏体实效钢飞轮在半径35.625 mm 处出现最大径向应力，且随着转速增加，径向应力值增大，当转速为15000 r/min时，最大应力值为658.36 MPa。由图10 可见，飞轮最大环向应力出现在半径142.5 mm 处，当速度为15000 r/min 时，最大应力为329.49 MPa，环向应力在半径范围内并非单调分布，两种应力都随转速增大而明显增大。

图9 马氏体实效钢飞轮不同速度下的径向应力Fig.9 Radial stress of martensitic steel flywheel at different speeds

图10 马氏体实效钢飞轮不同速度下的环向应力Fig.10 Ring stress of martensitic steel flywheel at different speeds

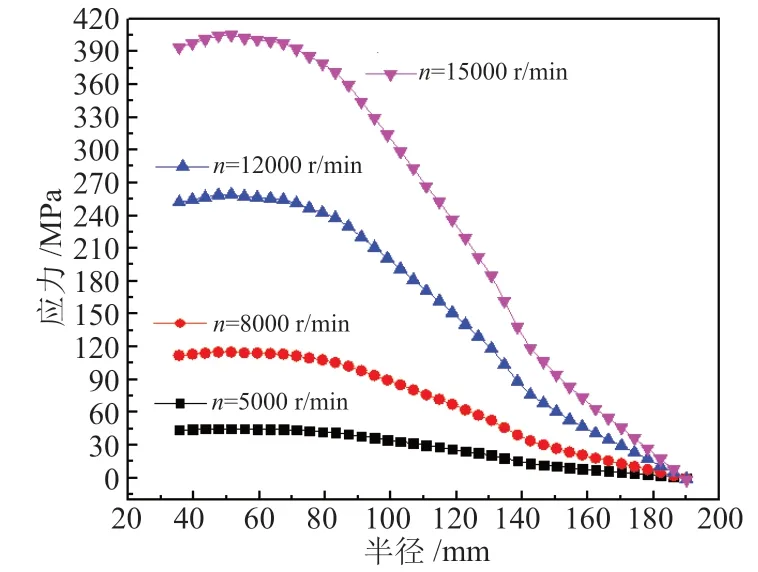
图11 钛合金飞轮不同速度下的径向应力Fig.11 Radial stress of titanium alloy flywheel at different speeds

同样地，如图11 和图12 所示，钛合金飞轮的最大径向应力出现在半径35.625 mm 处，应力值随着转速的增加而增加。当速度增加到15000 r/min时，最大径向应力为405.15 MPa。最大环向应力出现在半径142.5 mm 处，当速度为15000 r/min 时最大应力为201.85 MPa。

图12 钛合金飞轮不同速度下的环向应力Fig.12 Ring stress of titanium alloy flywheel at different speeds

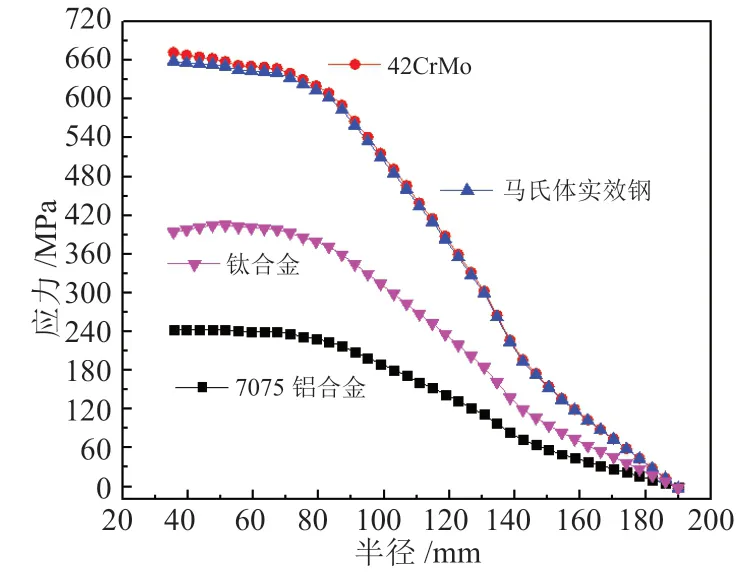
图13 四种飞轮材料径向应力变化曲线Fig.13 Variation curve of the radial stress of four kinds of flywheel

图14 四种飞轮材料环向应力变化曲线Fig.14 Variation curve of the ring stress of four kinds of flywheel

由上述分析可见，在相同的结构和速度情况下，对于4 种不同合金材料的飞轮，其应力变化规律相同，但应力的数值并不相同。

因此，为增加可比性，基于相同的速度条件对4 种不同飞轮材料的应力变化进行对比分析，结果将有助于选择飞轮材料并提高储能飞轮的性能。设置转速为15000 r/min，4 种飞轮材料的应力变化曲线如图13 和图14 所示。

从图13、图14 可以看出，对四种不同材料的飞轮设置的速度相同，评估其径向应力和环向应力，很明显,其中四种材料的变化曲线趋于一致，42CrMo 和马氏体实效钢产生应力最大。相反，7075 铝合金最小，7075 铝合金飞轮引起的应力对飞轮整体损伤最小，相比较而言，更适合制作储能飞轮。

4 结 论

本文以7075 铝合金材料飞轮为研究示例，研究了不同材料的储能飞轮在不同工作状态下的影响因素，通过ANSYS Workbench 软件，对不同材料的飞轮模型的应力进行对比，得到其对径向应力和环向应力的影响规律。得出以下结论：

（1）不同转速情况下，飞轮最大径向应力出现在内壁，向外逐渐减小，在转速15000 r/min 时，出现的最大应力为243.42 MPa；最大环向应力出现在飞轮轮缘与轮盘交汇处，最大值为122.61 MPa，随着转速增大应力值也增大；

（2）四种合金材料的比较，最大径向应力：42CrMo 是7075 铝合金的2.77 倍，马氏体实效钢是7075 铝合金的2.71 倍，钛合金是7075 铝合金的1.62 倍；最大环向应力：42CrMo 和马氏体实效钢是7075 铝合金的2.72 倍，马氏体实效钢是7075 铝合金的2.69 倍，钛合金是7075 铝合金的1.65 倍。

由以上结论可见，在相同结构和转速条件下，7075 铝合金以其轻便、径向应力和环向应力小，能保证飞轮运行的安全，优于其他3 种合金，为储能飞轮的结构设计和优化提供了重要参考。