数学语言助推数学抽象与直观想象*
——以数学概念教学为例
2019-12-11
(启东市汇龙中学,江苏 启东 226200)
如果说学习数学的终极目标是用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界,那么,无论“数学眼光”远近与高低,还是“数学思维”的深浅与宽窄,其实都需用“数学语言”来表达,“让不可见变成可见”[1].数学语言对培养数学抽象与直观想象能力起到不可或缺的助推作用,反之,通过数学抽象与直观想象又不断锤炼数学语言,甚至说,人类语言的产生和发展就是源于抽象能力和直观想象能力的发展.
数学语言古已有之,源远流长,其过程始终离不开“数学抽象”和“直观想象”,虽然当时并没有这两个数学术语.
人们在原始生活中逐渐抽象出数字,在公元前500年左右,数学主要是有关数字的一种学问,即古巴比伦和古埃及时期的数学.因此,在这些远古文明中,数学绝大多数都是以算术为主的.从大约公元前500到公元前300年的这一时期,是古希腊数学的时代,那时的数学家主要研究几何学,最经典的就是欧几里得撰写于公元前350年的《几何原本》,在第一册中,欧几里得利用后来被称为欧氏几何的一个有关定义与设推(公理)系统,企图捕捉平面上规则图形如直线、多边形与圆形的抽象模式.在我国,有一道古代数学名题“鸡兔同笼”,后来通过代数抽象建立了简单的方程组,得出了普遍意义上这类数学问题的解决方法.南北朝时期杰出的数学家祖暅沿用刘徽的数学思想,展开丰富的直观想象和数学抽象,利用“牟合理论”进行体积计算,得出“幂势相同,则体不容异”的结论,现称“祖暅原理”.
本文主要就概念教学的过程中,数学语言在培养数学抽象与直观想象能力的表征与助推作用,谈谈自己的感想.
1 数学语言与数学抽象
数学语言可分为抽象性数学语言和直观性数学语言,包括数学概念、术语、符号、式子、图形等.数学语言又可归结为文字语言、符号语言、图形语言.抽象性不是数学特有的,数学抽象是指舍去事物的一切物理属性,得到数学研究对象的思维过程,主要包括:从图形与图形关系、数量与数量关系抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出一般规律和结构,从而用数学术语或符号等予以表征.
数列的概念本身是从实际生活中抽象出来的一列有序的数字.等差数列的概念是在数列的基础上进行强抽象所形成的一个特殊的数列模型.正如上面所说,用数学语言表征一个比较完整的概念一般会经历文字语言、符号语言和图形语言这3个不同的阶段,下面以等差数列的概念教学为例.
在实际生活中常常会遇到这样一些特殊数列:
1)某学校小剧场有40排座位,第一排有16个座位,从第二排起,后一排都比前一排多2个座位,那么各排的座位数依次是
16,18,20,22,24,26,….
(1)
2)诺沃尔在1740年发现了一颗彗星,后来,人们推算这颗彗星将每隔83年出现一次,那么从发现那年算起,这颗彗星出现的年份依次为
1 740,1 823,1 906,1 989,2 072,….
(2)
3)第23届到第31届奥运会举行的年份依次为
1 984,1 988,1 992,1 996,2 000,2 004,2 008,2 012,2 016.
(3)
4)某钢材库新到一批规格相同的圆钢,现把它们堆成三角形垛,由于受到地域的限制,假如最下面一层放26根,从第二层起,每一层比下面一层少放一根,则从下往上堆放的圆钢数为
26,25,24,23,….
(4)
上面这些数列有什么共同点?用文字语言可表述为:如果一个数列从第二项起,每一项减去它的前一项所得的差都等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用d表示.
有人说数学的简洁就是美!但数学符号的简洁之处不仅仅是简单地用符号来代替文字.如果数列的一般形式写成a1,a2,a3,a4,a5,…,那么等差数列的特征就是a2-a1=a3-a2=a4-a3,…,即an+1-an=d,其中n∈N*,d是常数.这样的符号表示顿时解决了等差数列的连续等距的“任意性”问题,即从第二项起,每一项减去它的前一项所得的差都等于同一个常数.
又由an+1-an=an-an-1=d,适当变形得

图1
事实上,以现代函数的“对应说”也不难理解,数列的项数n与项an之间建立了一个函数关系f(n)=an,于是,一系列点(1,a1),(2,a2),(3,a3),…,(n,an)…,连成线必在同一条直线上(斜率相等),如图1.至此完成了等差数列的几何表征,也为后续学习和深入理解等差数列的通项公式埋下了伏笔.
2 数学语言与直观想象
直观想象,即“几何直观和空间想象”.它是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.主要包括:借助空间形式认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路.可以这么说,几何直观为空间想象提供了认识基础,空间想象为几何直观和由之向整体把握的发展提供了方法,是一嵌套循环的互动关系[2].
显然,直观想象不仅限于立体几何的教学中.下面以导数概念的起始小节中“平均变化率”为例,彰显数学语言在培养直观想象能力与素养的表征作用.
2017年10月江苏省南通市教育局组织的正高级职称评审过程的课堂评议环节在南通市第三中学举行,笔者为突出该课题中的“变化”两字,即兴改编了白居易《大林寺桃花》诗一首,感受大自然季节的交替“变化”.
三中校园桂香尽,人间菊花始盛开.
长恨秋归无觅处,原已转入此中来.
紧接着围绕课题中的关键词“变化率”,以几个场景(图略)彰显“变化”的快慢,以空间想象感知事物的形态与变化:
1)观光缆车(高度)变化“慢”与“快”;
2)万年银杏生长(变化)“缓慢”;
3)千年杉树生长(变化)“较快”.
数学是打开物理宇宙之锁的那把抽象钥匙.物理与数学往往结伴而行,为直观感知数学中的“平均变化率”,观察当年飞人刘翔的比赛场景,不难联想到“平均速度”的物理概念,即起步到第一个栏的平均速度,以及栏与栏之间的平均速度,逐步向“平均变化率”过渡.
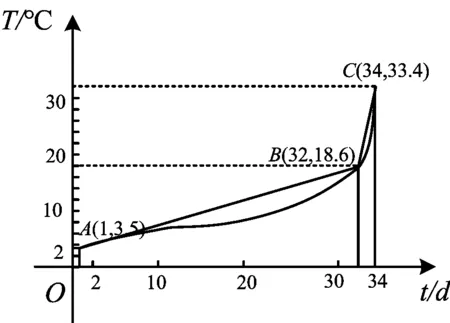
图2
有人说,数学源于生活,但关键是要逐步将生活场景“数学化”处理,并挖掘和表述现象背后的数学意义.人们有时会感觉气温骤冷骤热,图2是苏教版教材上的一张气温曲线图,不难看出点B,C之间的曲线较点A,B之间的曲线更加“陡峭”,显然,陡峭的程度反映了气温变化的快与慢.
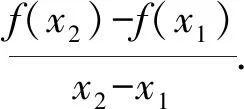

图3
也即曲线的割线AB的斜率.
但是,用平均变化率来量化一段曲线的陡峭程度是“粗糙不精确的”,但应注意当x2-x1很小时,这种量化便由“近似”逼近“精确”,因此随之而来的便是新的数学模型的建立,即瞬时变化率——导数的概念.
3 用数学语言可以描述“无限”
“孤帆远影碧空尽,唯见长江天际流”给了我们无限的空间与想象,而数学语言精确简洁表达,常常以“有限”的步骤来刻画数学对象的“无限性”和“任意性”.例如,数学归纳法原理,用有限的归纳假设和归纳递推,证明有关自然数的命题的无限成立.再譬如,单调性的判断与证明,需要定量描述图像呈上升(下降)的趋势,于是用符号语言表示为:在一个区间I内任意取两个实数x1,x2,若x1
诚然,在日常的概念教学中,数学语言可以助推数学抽象和直观想象能力的培养,但由于数学抽象的实现过程是通过一系列的比较和区分、舍弃和收括的思维操作实现的[3],因此,它是一个具体到抽象、抽象到具体的交替上升的过程.
数学的高度抽象性决定了数学抽象与直观想象远不止上述的概念教学那么简单.1736年,29岁的欧拉圆满地解决了“哥尼斯堡七桥”问题,他将岛与桥抽象成点与线,通过直观与想象,再用数学语言和思维开创了数学新的分支——图论,后来他使用过的一系列数学符号语言也一直沿用至今,堪称近代“数学语言家”.
