一种提高光纤旋转系统导航精度的扰动基座对准技术
2019-12-11袁书博扈光锋李邦清唐江河
袁书博,张 辉,扈光锋,李邦清,唐江河
(1.北京自动化控制设备研究所,北京 100074; 2.陆军装备部驻北京地区航空军事代表室,北京 100074;3.航天科工集团三院, 北京 100074)
0 引言
光纤旋转系统通常在交付使用之前进行标定从而获得误差参数并在导航时进行补偿[1],可以得到较高的导航精度。但是系统的误差参数并不是一成不变的,随着时间推移会发生改变[2-5]。对于高精度光纤旋转系统,3年时间标度因数误差可以变化3×10-4左右,安装误差变化60″左右。误差发生变化后,在进行旋转对准与旋转调制导航时,转位机构可以对惯性仪表的常值误差进行周期性的调制,从而提高系统的导航性能,但无法调制掉陀螺标度因数误差由于敏感地球自转角速率而产生的误差;并且旋转机构的转动会激励起陀螺标度因数误差与安装误差产生导航误差,当陀螺标度因数误差和安装误差等惯性器件误差较大时,在一个旋转周期内会引起的速度误差也会变大。
因此,光纤旋转系统在自对准的同时精确获得系统的陀螺安装误差和标度因数误差等误差参数,并对其进行相应的补偿,会减小速度误差,提高导航精度。本文研究了光纤旋转系统扰动基座条件下的自对准技术,提出了一种新的自标定自对准方案,即在自对准时使用少量时间对陀螺安装误差、陀螺标度因数误差、加表零偏进行标定,减小此误差引起的导航误差,从而提高旋转导航精度。
1 误差分析
1.1 旋转系统误差方程
旋转系统除了使用了常用的坐标系外,还采用了一个新的坐标系:旋转坐标系r系。旋转坐标系的定义为:该坐标系与惯性器件固连,原点O为惯性测量单元(Inertial Measurement Unit,IMU)的质心,初始时刻该坐标系与载体坐标系重合,指向载体的前、上、右。
由于旋转系统采用捷联导航算法,其误差方程本质上与捷联系统误差方程相同,区别仅在于增加了旋转调制矩阵,具体如下
(1)


(2)
1.2 锯齿形速度误差分析
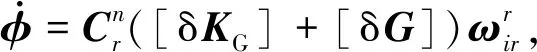
(3)

(4)
将式(4)积分可得在t时刻的数学平台失调角度,由于失调角的存在会产生重力加速度的投影误差,如式(5)所示
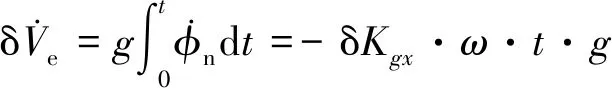
(5)
将该加速度误差积分即可得到系统速度误差
(1-cosωt)·δKgzx)·g/ω
(6)
由速度误差公式可知,陀螺安装误差形成的速度误差为线性增长项与正弦变化项的组合,陀螺标度因数误差形成的速度误差项为二次项。
在旋转360°时速度误差为
(7)
同理,当反向旋转360°时,陀螺安装误差与标度因数误差引起的速度误差为
(8)
反转1周产生的速度误差正好与正向旋转时产生的速度误差抵消。因此,通过旋转调制,在正反各转1周时,IMU转动会激励陀螺安装误差和标度因数误差使系统产生锯齿形的速度误差,误差最大值在正转360°时产生,可以通过减小或精确补偿陀螺安装误差与标度因数误差来减小锯齿形速度误差的振荡幅值。
1.3 旋转调制中陀螺标度因数误差效应研究
对于光纤陀螺来说,标度因数误差会随着时间而改变,长时间变化量可达上百ppm。在以地理系为旋转调制导航坐标系的情况下,该误差无法被调制掉,会敏感地球自转角速率进而产生导航误差,分析如下:

(9)
当IMU绕天向轴以角速率ω旋转时,t时刻陀螺的输入角速率为
(10)
由标度因数误差引起的数学平台角速率误差为
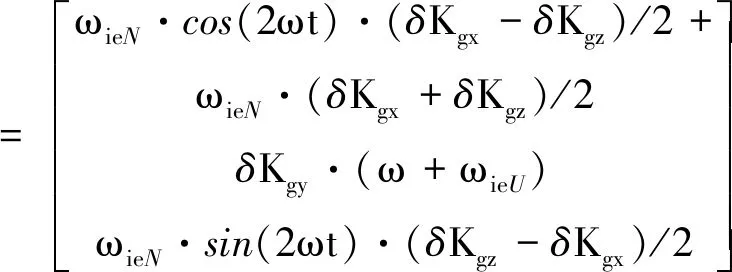
(11)
当旋转时间为T=2π/|ω|时,对式(11)进行积分可以得到旋转1周引起的平台误差角为
(12)
由式(12)可以看出,当IMU进行正反向旋转时,可以调制掉IMU旋转与标度因数误差产生的数学平台角度误差;而标度因数误差敏感到地球自转角速率产生的误差总是存在,无法将其调制掉。
因此,在系统使用前对陀螺标度因数误差进行标定,可以减小陀螺标度因数误差敏感地球自转角速率而产生的系统导航误差。
2 自标定自对准技术
目前光纤旋转系统普遍采用通电启动后,直接开始自对准流程,然而系统经过一段时间后,由于应力释放等原因,系统的安装误差和标度因数误差等都会发生变化。根据统计,3年时间标度因数误差最大可以变化3×10-4左右,安装误差最大变化60″左右。根据第1节可知,当陀螺标度因数误差和陀螺安装误差等误差较大时会引起较大的速度误差,因此需要结合光纤旋转惯导的特点研究适合工程应用的、可以提高系统导航精度的自对准方案。
结合光纤旋转系统的特点,本文提出了一种基于连续旋转自对准与快速自标定相结合的自对准技术。此时系统处于静止状态,系统基座为扰动基座,在自对准的同时对关键误差参数进行标定,从而减小误差对导航的影响,提高导航精度。本文自标定自对准的实现方案如图1所示。
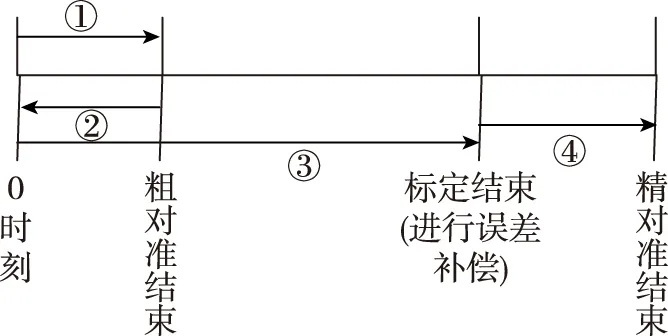
图1 自标定自对准实现方案图Fig.1 Self-calibration and self-alignment implementation scheme
1)读取IMU原始数据,采用抗扰动粗对准方法实现粗对准,确定惯导系统粗略初始姿态,记粗对准结束时刻为ts;
2)利用逆向导航算法[9-11],从ts到0时进行反向导航,对系统参数误差进行辨识,直到0时刻;
3)以逆向导航结束时的速度、位置和姿态信息为初始条件,从0时刻开始进行正向导航,同时继续进行卡尔曼滤波运算,辨识系统误差参数,直到标定结束,对系统关键的误差参数进行标定;
4)以标定结束时的姿态为精对准的初始姿态,并对误差参数进行补偿,进行连续正反转精对准。
2.1 自标定参数选择
陀螺相关误差为惯导系统主要的误差源,在系统使用前进行标定可以大幅提高导航精度。根据第1节分析可知,陀螺标度因数误差和陀螺安装误差会导致系统产生锯齿形的速度误差,并且陀螺标度因数误差敏感地球自转角速率而引起的姿态误差不能被调制,另外加表的零偏对导航也会产生一定影响。因此,本方案将选取陀螺标度因数误差、陀螺安装误差和加表零偏作为自标定参数。
2.2 自标定自对准路径及可观测度分析
根据选定的标定参数,设计了一个自标定自对准转位路径,通过控制旋转机构使IMU按设计路径进行转动[12-13],使系统在自对准时完成对选取参数的标定,整个过程用时615s。
对路径采用基于奇异值分解的可观测性分析方法对系统误差的可观测度进行分析,结果见表1。由表1可知,在该路径的激励下,除δkgzx外,其他的陀螺标度因数、陀螺安装误差和加速度计的零偏具有较高可观测度,可以实现这些参数误差的标定。
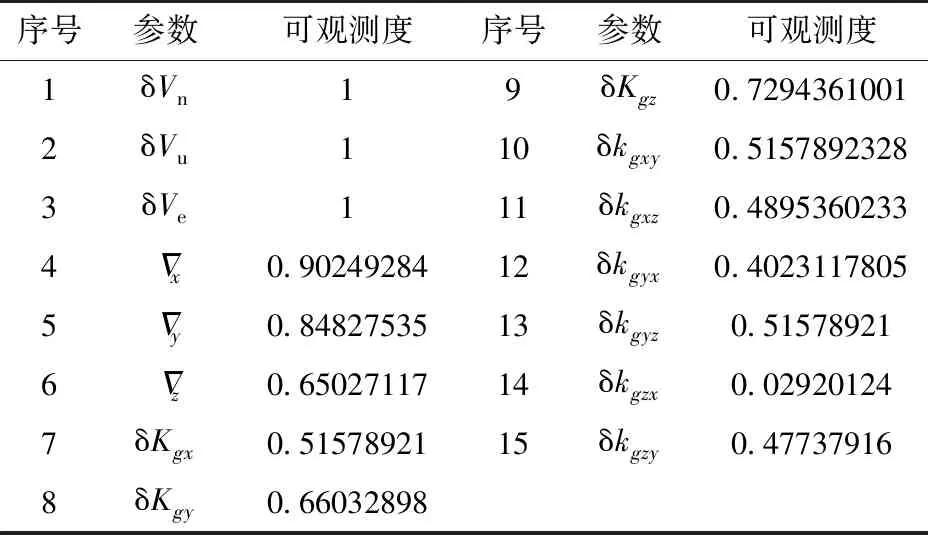
表1 标定参数可观测度统计
2.3 自对准滤波模型
根据该误差方程,设计Kalman滤波器,在自对准过程中选取不同的滤波器进行误差参数标定与系统对准,其主要区别在于滤波器状态变量的选取。
对于标定滤波器,根据惯性导航系统误差方程和器件误差模型,选取速度误差、姿态误差以及待标定的器件误差参数作为滤波器的状态变量
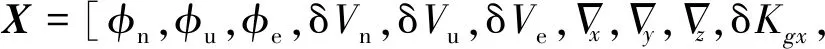
对于对准滤波器,由于在对准过程中产生速度误差的主要误差源为加速度计零偏与陀螺漂移,所以选取速度误差、位置误差、姿态误差、加速度计零偏、陀螺漂移为滤波器的状态变量
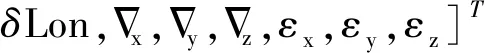
2.4 自标定自对准工程实现
为了缩短系统的准备时间,在进行粗对准时存储粗对准数据,通过在线反向导航实现粗对准数据的重复利用。在自标定与自对准进行切换时,使用标定结束时的姿态作为精对准的初始姿态,并对标定得到的误差参数进行补偿。
与目前光纤旋转系统普遍采取的在系统使用之前只进行连续旋转自对准的方案相比,该自标定自对准方案可以在对准之前用350s对陀螺标度因数误差、陀螺安装误差和加表零偏进行估计补偿,从而提高了系统的对准与导航性能。
3 数学仿真与工程试验验证
3.1 自标定自对准数学仿真
3.1.1 仿真条件
利用Matlab搭建了自标定自对准数据发生器,数据发生器参数设置如表2所示,初始姿态设置如表3所示。
利用数据发生器生成自标定自对准方案陀螺与加速度计的采样值。
3.1.2 仿真结果及分析
首先对本文的自标定自对准流程进行仿真,标定的仿真结果如图2所示。
仿真标定估计值与真值的对比如表4所示。
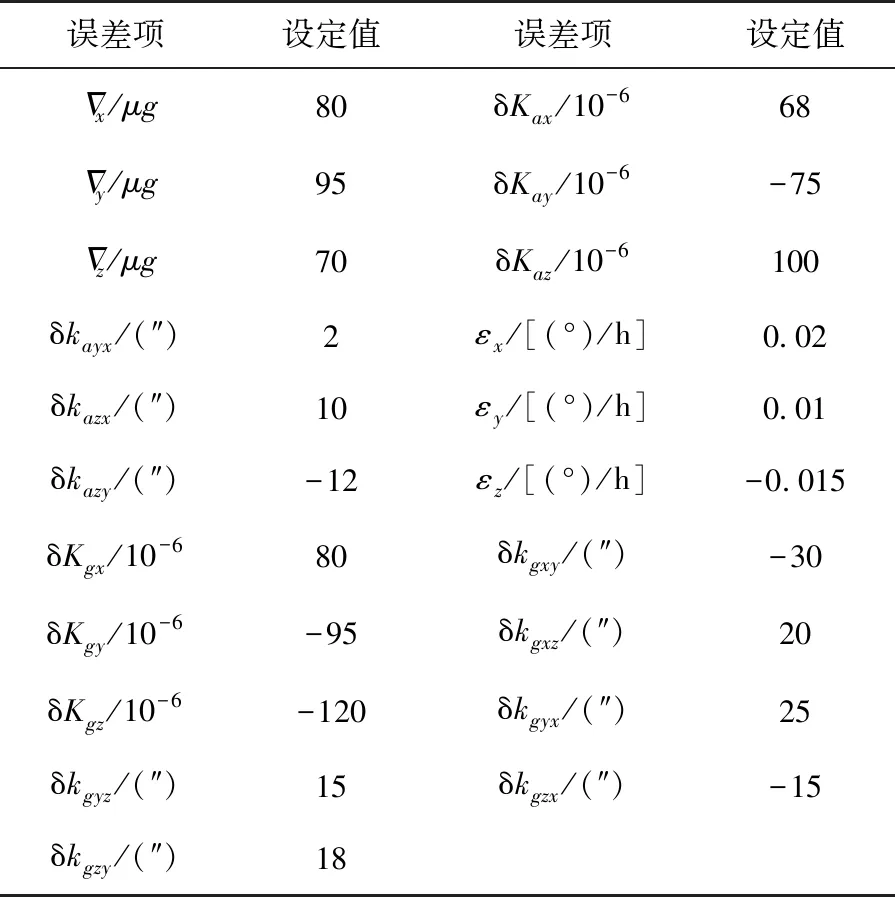
表2 误差参数设定值

表3 初始姿态
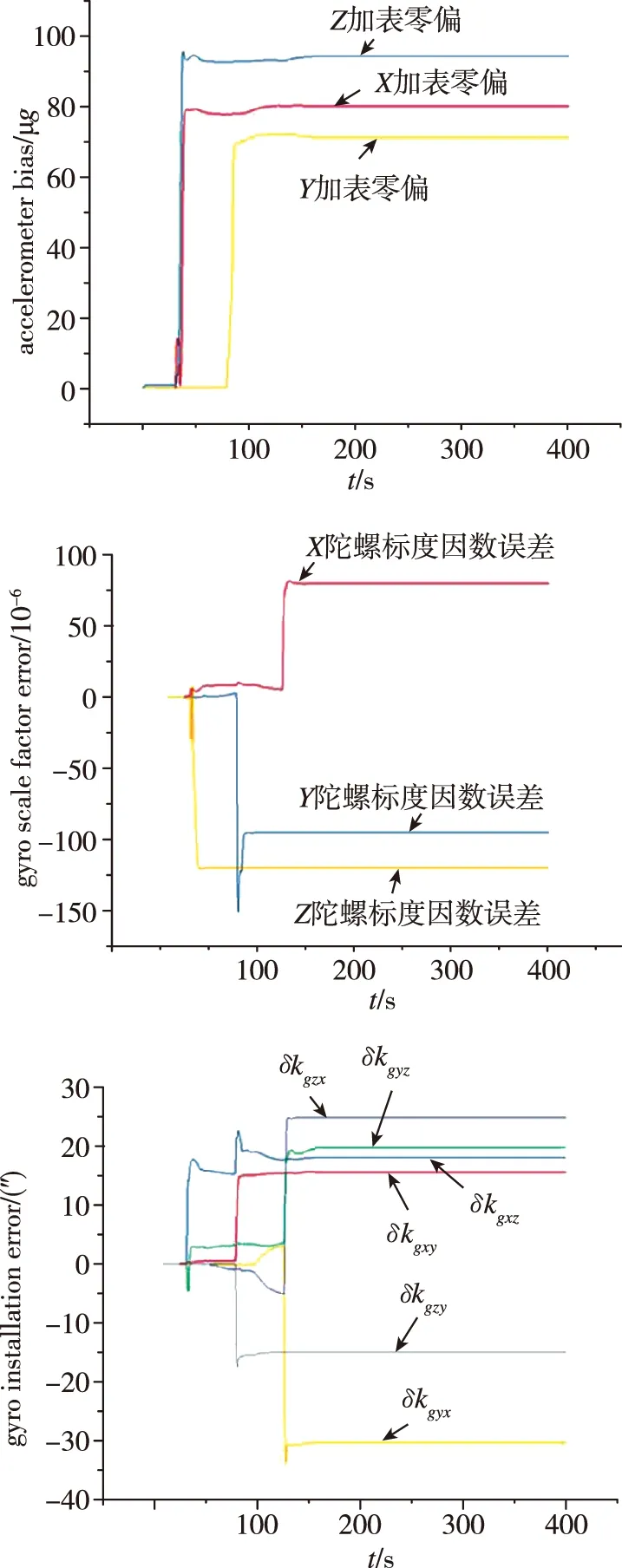
图2 标定结果Fig.2 Calibration results
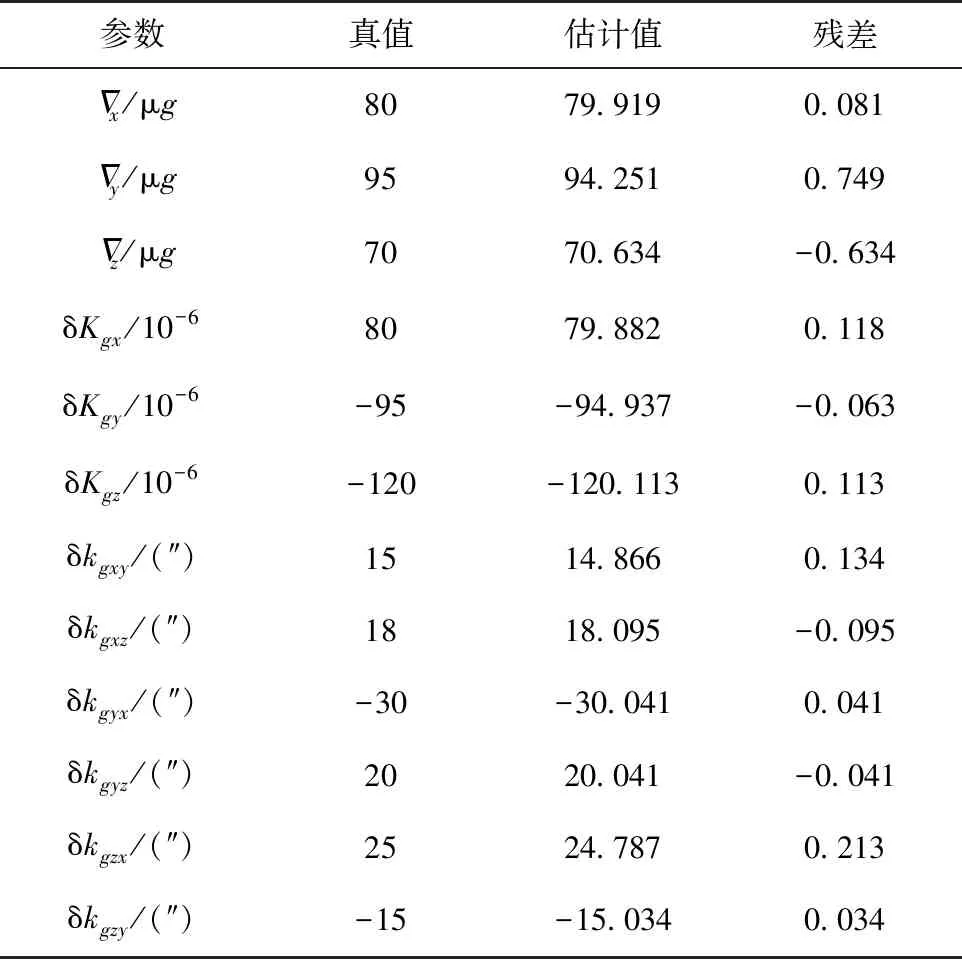
表4 标定参数估计值
由表4可以看出,该自标定自对准方案在615s内实现了对陀螺的标度因数误差、陀螺安装误差和加速度计零偏的准确估计,其最大残差分别为0.749μg、0.118×10-6、0.213″,同时完成了系统对准,对准结果与使用10min连续正反转自对准处理流程的对准结果对比如表5所示。

表5 对准结果
表5表明,使用自标定自对准流程可以提高对准精度。
为了直观地显示该方案的效果,将本文的自标定自对准方案作为对准方案应用到静止的十六位置旋转调制[16]导航中,与采用10min连续正反向旋转对准方案的十六位置旋转调制导航进行对比。导航时间为3.3h,速度误差分别如图3和图4所示,2组导航试验结果如表6所示。

图3 使用自标定自对准流程的导航误差Fig.3 Navigation errors by self-alignment and self-calibration

图4 使用自对准流程的导航误差Fig.4 Navigation errors by self-alignment

表6 导航结果
可见,系统处于旋转调制状态导航时,使用自标定自对准流程后,速度误差有所下降(北向速度最大误差值由-0.87m/s降至-0.004m/s,东向速度最大误差值由-0.8m/s降至0.006m/s),且锯齿现象明显降低,导航性能明显提升。
3.2 试验验证
3.2.1 试验条件
采用某台长时间未进行标定的光纤旋转惯导系统进行工程试验验证,将其稳定放置于试验台上,经自标定自对准流程后转双轴十六位置旋转调制导航,导航1.4h。
首先对自标定结果进行分析,为了验证该方案标定的精确度,将使用本文标定路径的结果以及使用十九位置标定的结果作比较,如表7所示。

表7 标定参数估计值
由表7可以看出,使用本文标定路径与使用十九位置标定的标定结果基本一致,其最大残差分别为8μg、3×10-6、5″,能够反映出系统误差参数的变化。
利用十六位置旋转数据,对使用本文自标定自对准流程的导航误差与使用10min连续正反转自对准流程的导航误差进行对比,分别如图5和图6所示。
由图5和图6可见,在旋转调制状态,使用自标定自对准流程后的导航速度误差有所下降,导航精度得到提高。
将以上导航试验结果统计于表8中。
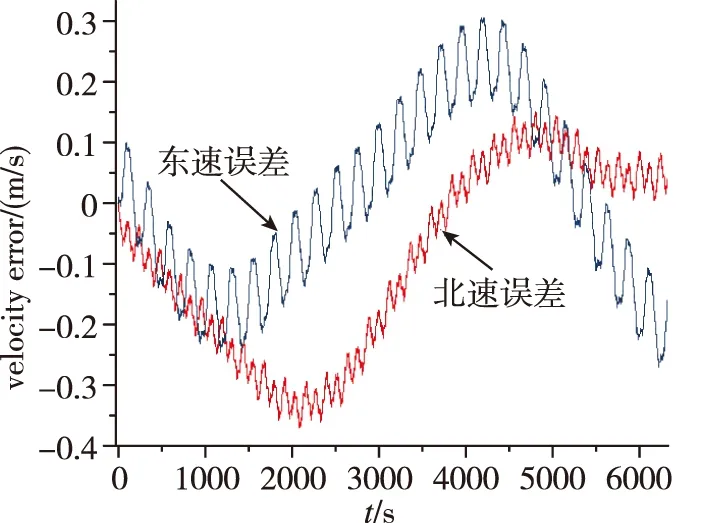
图5 使用自标定自对准流程的导航误差Fig.5 Navigation errors by self-alignment and self-calibration
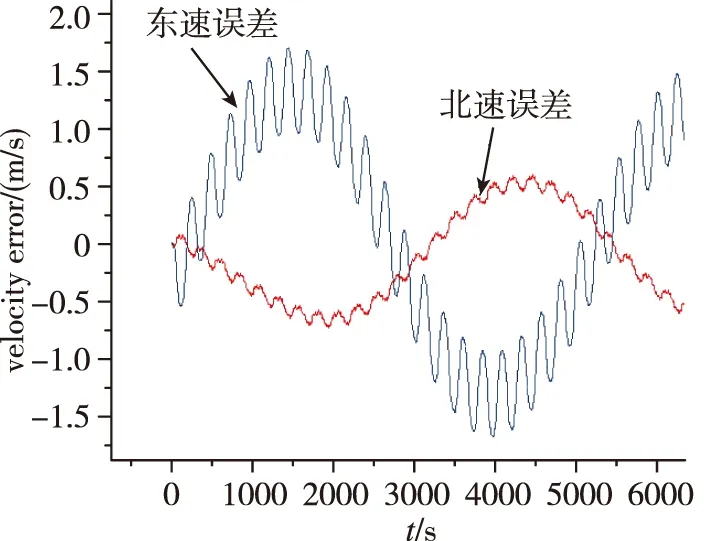
图6 使用自对准流程的导航误差Fig.6 Navigation errors by self-alignment
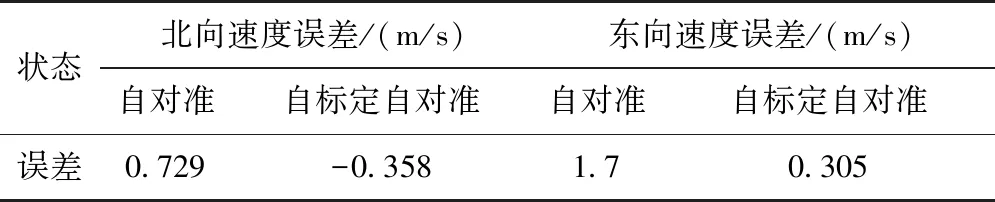
表8 导航精度
由表8可见,使用本文自标定自对准流程后,北向速度最大误差值由0.729m/s下降至-0.358m/s,东向速度最大误差至由1.7m/s下降至0.305m/s,可见本文所提自标定自对准方法可以减小旋转调制的速度误差,提高旋转调制的导航精度。
4 结论
为了提高光纤旋转系统导航及对准精度,本文对光纤旋转系统扰动基座自对准技术进行了研究,提出了一种自标定自对准方案。首先结合光纤旋转系统特点分析了误差参数对旋转调制导航的影响。其次选择标定参数并根据标定参数设计了特定的系统转位路径,实现了对陀螺标度因数误差和陀螺安装误差、加表零偏的标定与系统自对准。最后通过数学仿真与工程试验验证表明,使用该自标定自对准流程与使用10min连续旋转自对准流程相比,系统北向速度误差减小50%以上,东向速度误差减小80%以上。
