分形塔分抗逼近电路——标度拓展与优化设计原理

张月荣， 袁 晓， 郭钊汝

(1.四川大学电子信息学院， 成都 610064； 2.新疆农业大学计算机与信息工程学院， 新疆 830052)

1 引 言

分数阶微积分已逐步发展为数学分析中的一个重要领域[1]. 近年来，随着分数阶微积分研究的深入，分数阶线性系统，分数阶混沌系统，分数阶流变模型，分数阶忆阻器[2]等相关电路模型的研究与应用越来越广泛[3]. 分数阶电路与系统更能刻画实际的物理工程现象. 分数阶电路与系统中的核心电路元件就是分抗(元)[4]. 理想分抗(元)的阻抗(或导纳)函数可表示为

I(μ)(s)=F(μ)·sμ，(0<|μ|<1),s∈

(1)

式中，s为拉普拉斯变量，也称频率运算变量；μ表示分抗元的运算阶，当运算阶取值为分数时，称sμ为分数阶算子；F(μ)为分抗元的集总特征参量，称为分抗值(简称分抗，fractance). 为便于数学分析而又不失一般性，往往将分抗元的阻抗函数进行归一化处理. 定义归一化运算变量

(2)

式中，τ=RC，表示时间常数； Ωτ为特征频率值. 归一化后分抗元的阻抗函数为

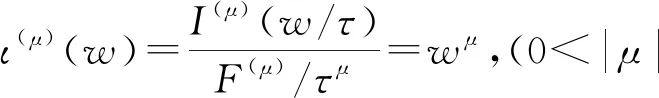
(3)

鉴于实际因素和现有的工艺制作手段，工程上主要考虑由整数阶电路元件(电阻，电容，电感)构建具有分数阶运算性能的无源网络来近似实现分抗元的运算功能[5]，这类电路模型被称为分抗逼近电路. 现有的许多经典无源分抗逼近电路(例如Oldham分形链分抗，Sierociuk分形链分抗，Carlson分形格分抗等)都能在特定的频率范围或条件下实现分数阶运算性能. 这种在特定频率范围或一定条件下逼近理想分抗的过程被称为非理想分抗逼近过程.

文献[6]在对比分析Oldham分形链分抗与Liu-Kaplan分形链分抗的基础上，发现描述Liu-Kaplan分形链分抗的代数迭代方程可由描述Oldham分形链分抗的代数迭代方程标度化得到. 由此，袁晓提出标度拓展理论. 标度拓展可将原负半阶逼近的分抗拓展为任意阶分抗逼近，降低电路设计成本. 另外，逼近性能的提升也可由对原电路的优化实现[7-8]. 例如改进Oldham I型分形链分抗[4]，对比原电路，改变第一个电阻的取值能够极大提高逼近效益. 经典的分抗大多为容性分抗(运算阶为负)，感性分抗(运算阶为正)具有同等应用价值. 然而电感自身具有不适宜集成的特性，尤其单片集成电路不能制作电感，因此感性分抗极少被研究及应用. 如何构造感性分抗逼近电路也是分抗实际应用时急需解决的问题[9].

本文在分析负半阶B型分形塔分抗电路的基础上，根据标度拓展理论，分析原电路标度拓展后的分数阶运算性能，得到具有任意分数算子的标度分形塔分抗逼近电路. 并针对标度拓展后的电路在一定频段处逼近失真的问题，探寻标度分形塔分抗的优化原理及方法. 分析标度拓展后电路的振荡现象. 提出由电阻，电容和运算放大器构建的有源电路网络实现感性分抗(0<μ<2)的方法. 通过理论分析与仿真实验，证明塔形分抗标度拓展的运算有效性和电路优化方法的可行性.

2 标度拓展——任意阶标度分形塔分抗

2.1 B型分形塔分抗逼近电路及其标度拓展

文献[5]提出了一种不同于经典Oldham分形链分抗和Carlson分形格分抗的负半阶分抗逼近电路——B型分形塔分抗逼近电路. 该RC分抗逼近电路是实现负半阶积分算子的理想逼近，其迭代电路原理图及归一化迭代电路如图1.

B型分形塔分抗迭代算法公式为

(4)

式中，k表示电路的迭代次数，也是电路级数. 正如Oldham分形链分抗与Liu-Kaplan分形链分抗，标度拓展后，描述半阶算子的代数迭代方程可转化为描述任意阶算子的非正则标度方程.

代数迭代方程非正则标度方程

F(α±1y(σ±1w))

(5)

式(5)中的α，β称为电路的标度特征参量，取正实数.σ=αβ称为标度因子. 当1<σ<∞时为正比标度拓展，简称正比拓展；当0<σ<1时为反比标度拓展，简称反比拓展. 根据拓展理论，B型分形塔分抗标度拓展后，理论上可以实现任意阶分数算子的有理逼近. B型分形塔分抗归一化迭代电路及其标度拓展后的迭代电路如图2，对应的非正则标度方程如式(6).

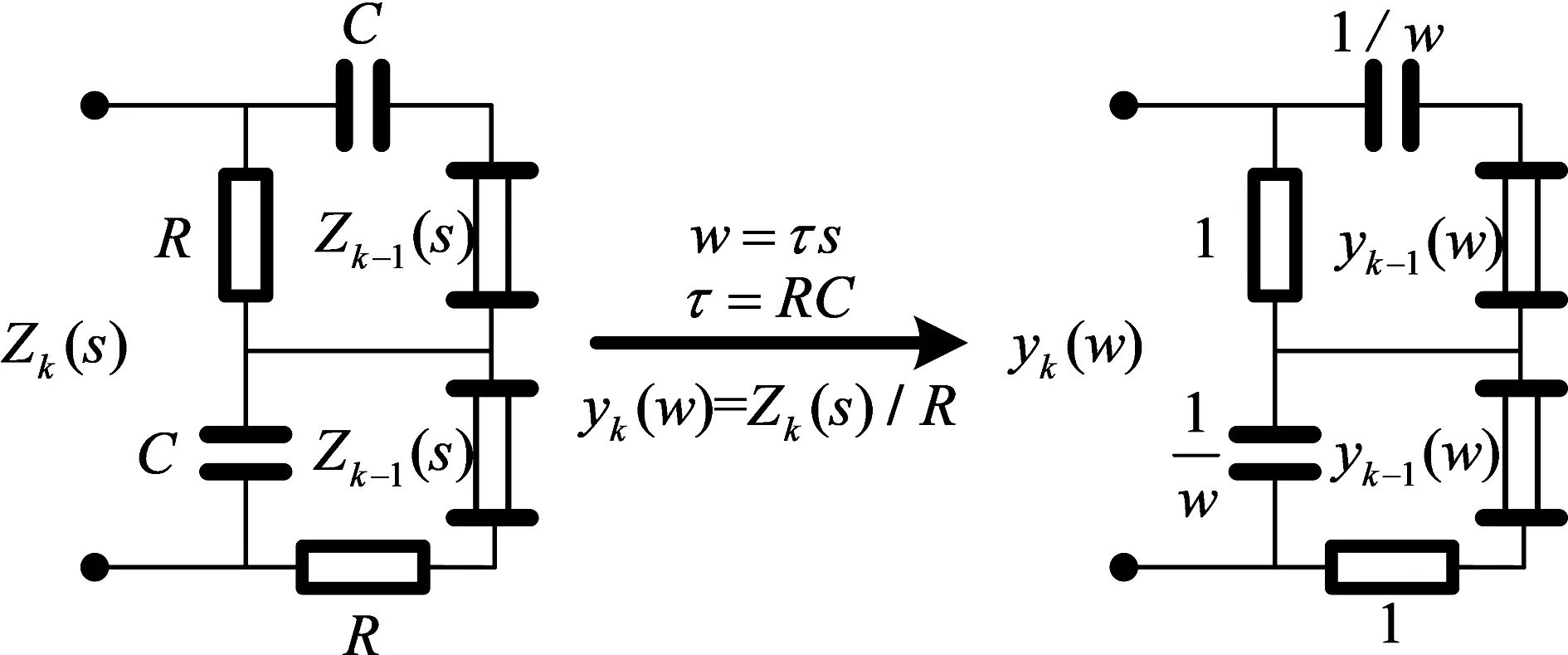
图1 B型分形塔分抗迭代电路与归一化迭代电路Fig.1 B-type fractal-pyramid fractance iterating circuit and normalized iterating circuit

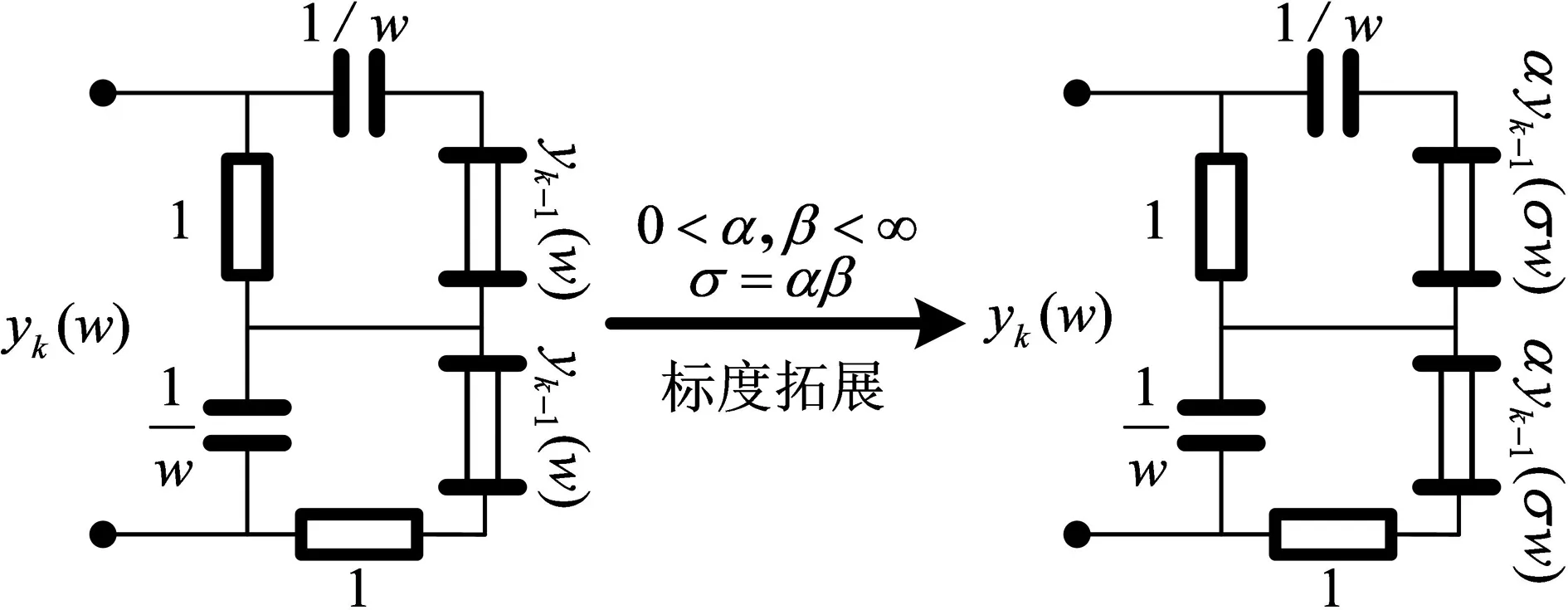
图2 B型分形塔分抗标度拓展电路图Fig.2 Scaling extension circuit diagram of B-type fractal pyramid fractance approximation circuit

图2在正文没有描述，请先描述再有图出现.

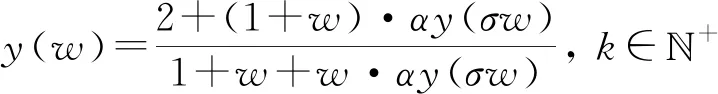
(6)

非正则标度方程(6)是一种双重标度方程. 该代数迭代方程完全表征和描述了标度分形塔分抗逼近电路的运算性能和电气响应特征[10]，标度分形塔分抗逼近电路的结构特征蕴含在该双重标度方程中. 该电路的极限阻抗必定为式(6)中方程的一个真实解. 求解该方程对分析分抗电路特征具有重要作用[11].

2.2 分形塔分抗的运算有效性及频域特征函数

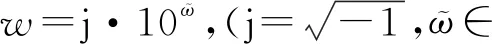
yk(j·10ϖ)=Ak(ϖ)·ejθk(ϖ),k∈,ϖ∈

(7)

式中幅频特征函数：

Ak(ϖ)=|yk(j·10ϖ)|

(8a)

或Λk(ϖ)=lg(Ak(ϖ)),ϖ∈

(8b)

相频特征函数

θk(ϖ)=arg {yk(j·10ϖ)},ϖ∈

(9)

阶频特征函数

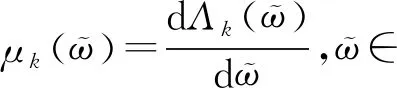
(10)

为便于在频域定量分析分抗逼近电路的集总特征值F(μ)，文献[12]提出F特征函数：

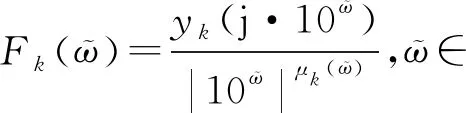
(11)

幅频特征函数和相频特征函数表征了分抗逼近电路阻抗函数的频域特征. 阶频特征和相频特征可完全表征分抗逼近电路的运算特征. 对于一个给定的分数阶系统，首先应该考虑它的运算阶[9]. 阶频特征是幅频特征的微分，因此阶频特征包含了幅频特征的信息. F特征描述分抗集总特征参量与频率ϖ的依存关系，在分抗逼近电路具体设计及实际应用中具有重要作用.

运算有效性[4]是指给定的分抗逼近电路，其极限阻抗，即描述其有理逼近过程的非正则标度方程

y(w)=F(αy(σw))

(12)

的解y(w)中，是否含有代数因子wμ(0<|μ|<1)也即分数算子. 标度分形塔分抗逼近电路显然是物理可实现的. 运算有效性的判定是研究分抗有理逼近问题或研究标度方程描述的过程或系统的核心问题之一. 判定标度分形塔分抗的运算有效性需求解方程(6)，该非正则标度方程的解析求解[13]具有一定的挑战性，还不知道如何实现. 因此，可考虑近似求解法.

2.3 近似求解与数值求解

根据近似求解结果可从理论上判断标度拓展后的B型标度分形塔分抗的运算有效性[14]. 数值求解[15]则可验证近似求解的正确性，并利于直观分析运算性能和逼近性能. 当电路迭代次数k→∞，在较低频段时|w|→0，电路中的电容容抗1/w→∞，此时电容近似开路状态. 根据归一化迭代电路，此时的归一化阻抗函数

(13)

在较高频段时，电路中的电容容抗1/w→0，此时电容近似为短路状态. 由归一化迭代电路近似求解的阻抗函数为：

(14)

正则标度方程(13)，(14)有近似解析解——Liu氏粗解

(15)

近似解(15)表明拓展后，标度分形塔分抗理论上可实现任意负分数阶算子的有理逼近. 运算阶只与α，β有关.

分抗逼近电路阻抗函数的数值求解常用算法有三种：传输参量矩阵法[10]，系数矢量迭代法[16]和标度矩阵迭代法[17]. 鉴于标度分形塔分抗电路结构特点，传输参量矩阵法不易于求解，因此考虑系数矢量迭代法或标度矩阵迭代法[18].不同初始阻抗下，两种算法的初始迭代参数如表1.

表1 初始阻抗对应的初始迭代参数

初始阻抗取值会影响标度分形塔分抗的零极点个数和分布情况，进而影响运算特征曲线的形状[19]. 初始阻抗为开路和短路时，两种算法求解的正比拓展时负半阶标度分形塔分抗运算特征曲线关于直线μLiu=-1/2对称(图3(a)和(b)). 当y0(w)=1/w时，由系数矢量迭代法求解的运算特征曲线偏离真实值(图3(d))，此时求解的零极点分布极不均匀.y0(w)=1时，两种算法求解的运算特征曲线几乎重合(图3(c)).

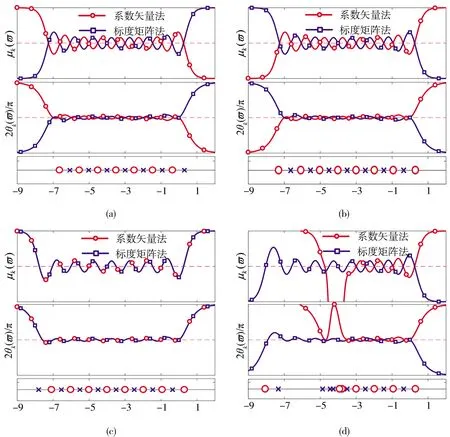
图3 正比拓展时不同初始阻抗下运算特征和零极点分布(μLiu=-0.5,k=12,σ=5σ=10)

对比分析发现，系数矢量迭代法计算速度较快[15]，当电路迭代次数k的取值较大时，标度矩阵迭代法将不太适用. 且表1中标度矩阵迭代法的初始阻抗迭代参数与电路迭代次数k有关,当迭代次数变化时，需要对初始阻抗中的σk进行指数调整[19]. 考虑到标度调整，优先选用系数矢量迭代法. 取y0(w)=1，由系数矢量迭代法求解拓展前后的分抗运算特征曲线如图4.

数值仿真结果表明，标度拓展前B型分形塔分抗是全频有效的半阶积分算子的理想逼近. 标度拓展后，该分抗可实现任意阶负分数算子的非理想逼近.

3 标度分形塔分抗的优化

很多经典的半阶分形分抗标度拓展后都能实现任意阶分数算子的逼近. 例如标度分形格分抗[1]，标度分形梯分抗[2-3]，标度分形串分抗[9]，标度分形链分抗类[16]等. 这些标度拓展后分抗的逼近效果都有待优化.图4(b)中的运算特征曲线表明，正比拓展较高频段(反比拓展较低频段)时，逼近效率不甚理想. 因此，通过电路优化[4]改善分抗逼近性能显得尤为必要[5]. 例如改进Oldham I型分形链分抗，电路上的微小改进便可获得逼近性能的极大改善.

3.1 电路优化理论分析

正比拓展时，随着迭代次数k的增加，逼近带宽向低频段延伸. 且频率取值越小，逼近性能越好. 反比拓展时，随迭代次数的增加，逼近带宽向高频段延伸. 频率取值越大，逼近性能越好. 但两种拓展情况下在w=1(频率指数ϖ=0)附近的逼近效果都有待优化. 根据不同运算阶下运算特征曲线的形状不同，结合运算阶μLiu及不同频段内电阻和电容的电学特性，分正，反比拓展两个方面理论分析标度分形塔分抗逼近电路的优化原理.

正比拓展(1<α,β,σ<∞)逼近频段向低频延伸. 当-0.5<μLiu<0时，在逼近频带的较高频段，运算特征曲线向μLiu=-0.5方向偏移，偏向电容的运算特征(电容的运算阶为-1阶)，优化补偿元件选用电阻(电阻的运算阶为0阶). 当-1<μLiu<-0.5时，在较高频段运算特征曲线向μLiu=-0.5方向偏移，偏向电阻的运算特征，优化补偿元件选择电容. 考虑较高频段时串联电容的容抗几乎可忽略，故选用并联电容，串联电阻的优化补偿网络.

反比拓展(0<α,β,σ<1)逼近频段向高频延伸. 当-0.5<μLiu<0时，在较低频段运算特征曲线向μLiu=-0.5方向偏移，即偏向电容的运算特征，优化元件选用电阻. 当-1<μLiu<-0.5时，在较低频段运算特征曲线向μLiu=-0.5方向偏移，偏向电阻的运算特征，优化元件选择电容. 而较低频段时并联电容的容抗几乎可忽略，故采用串联电容，并联电阻的优化补偿网络.

3.2 优化电路及优化频域曲线

选择对称阻容T型节对原电路进行补偿(如图5所示)，正比拓展时优化电路的补偿元件参数

(16)

反比拓展时电路优化原理图如图6，优化元件参数

(17)

取初始阻抗y0(w)=1,正比拓展时优化后的运算特征曲线如图7，其中黑色曲线为标度分形塔原型电路的运算特征曲线，红色为电路优化后的运算特征曲线.反比拓展时优化电路具有相同的频域优化效果.

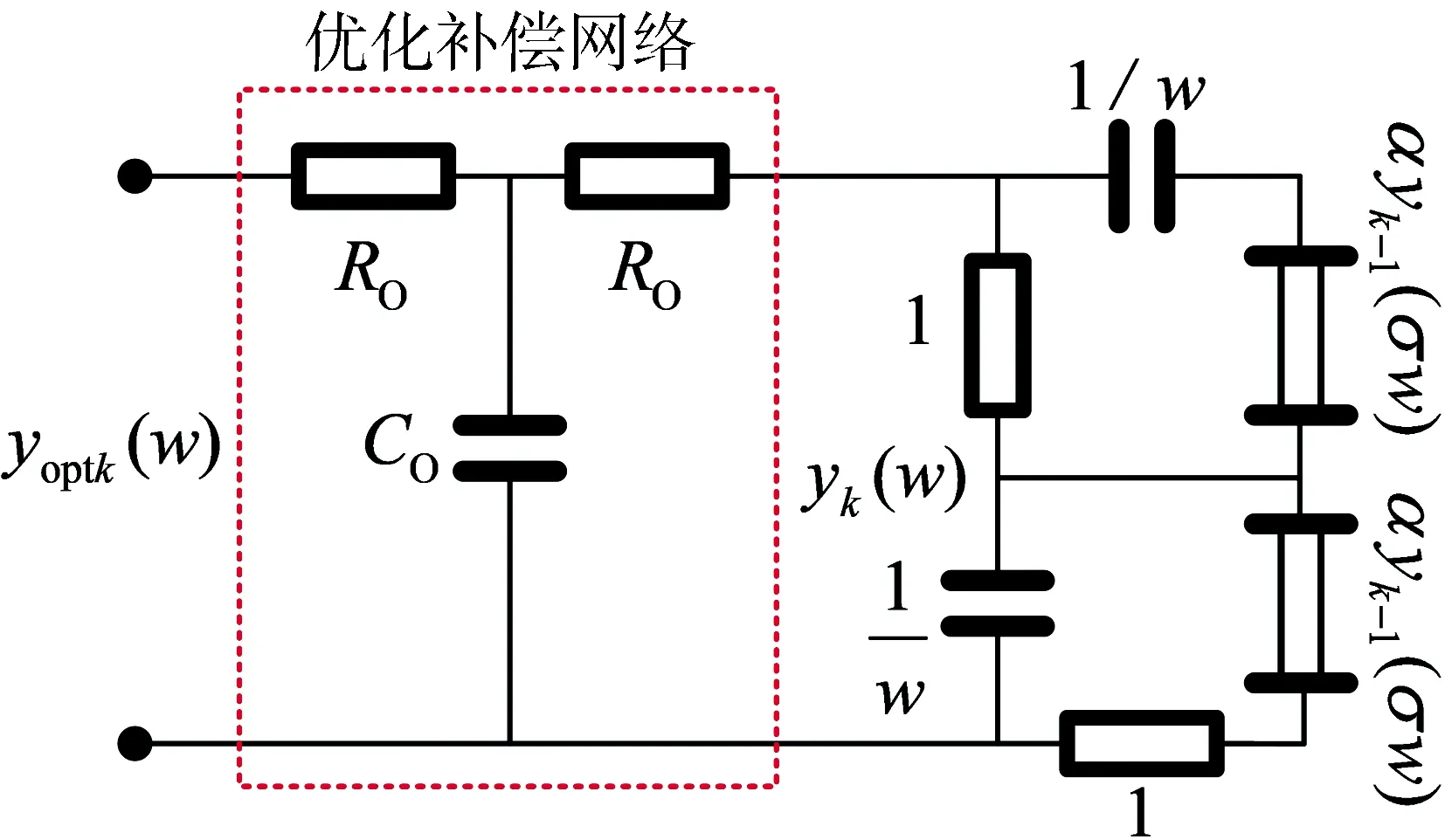
图 5 正比拓展优化原理图Fig.5 Optimization schematic diagram of direct proportion extension

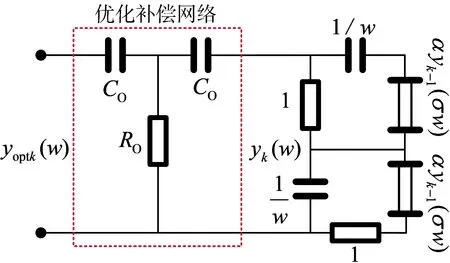
图6 反比拓展优化原理图Fig.6 Optimization schematic diagram of inverse proportion extension

4 优化标度分形塔分抗的频域特征及逼近性能

对比分析图7, 优化后的电路相比原型电路逼近理想分抗元的效果更好[6]. 尤其是运算阶μLiu≠-0.5时，优化后的逼近性能得到显著提升.

4.1 频域特征——运算振荡现象

电路的优化并无法消除或减弱逼近频带内的振荡现象，振荡现象是标度分形塔分抗所固有的[7]. 在工程应用中，必须考虑频域的振荡现象带来的逼近误差，因此需定性与定量分析标度分形塔分抗的运算振荡现象[8].

以正比拓展为例，在有效逼近频带范围内(如图8所示)，优化前后频域振荡波形具有固定振荡周期W=|lgσ|.

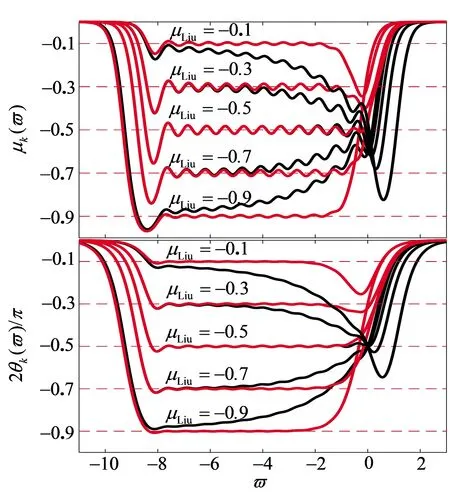
图7 正比拓展优化前后运算特征曲线对比图(k=12,σ=5)

随着标度因子的增加，逼近频带内波形振荡幅度也在增加(图8(b)). 标度因子σ取定值时振荡波形的幅度ξ与运算阶μLiu有关(图4(b)).图9分别展示了频域振荡波形幅度ξ与标度因子σ和运算阶μLiu之间的关系曲线.

运算阶μLiu一定时，振荡波形的幅度ξ与标度因子σ近似为线性关系(图9(a)). 且运算阶μLiu为(-1<μLiu<0)与(-1-μLiu)时运算特征曲线的振荡幅度曲线几乎重合. 阶频特征曲线与相频特征曲线的振荡幅度的拟合直线函数表达式为

ξO(μLiu,σ)=KO(μLiu)·σ+bO(μLiu)

(18a)

ξP(μLiu,σ)=KP(μLiu)·σ+bP(μLiu)

(18b)

式中，K(μLiu)为拟合直线的斜率；b(μLiu)为拟合直线与纵轴的交点. 拟合直线函数的斜率KO(μLiu),KP(μLiu)，截距bO(μLiu),bP(μLiu)与运算阶μLiu的函数关系拟合式为

KO(μLiu)=0.0228·sin(π(μLiu-1))

(19a)

bO(μLiu)=-0.0787·sin(π(μLiu-1))

(19b)

KP(μLiu)=0.0055·sin(π(μLiu-1))

(19c)

bP(μLiu)=-0.0220·sin(π(μLiu-1))

(19d)

函数表达式中参数的取值由数值拟合求得. 拟合函数中参数的图像如图10.

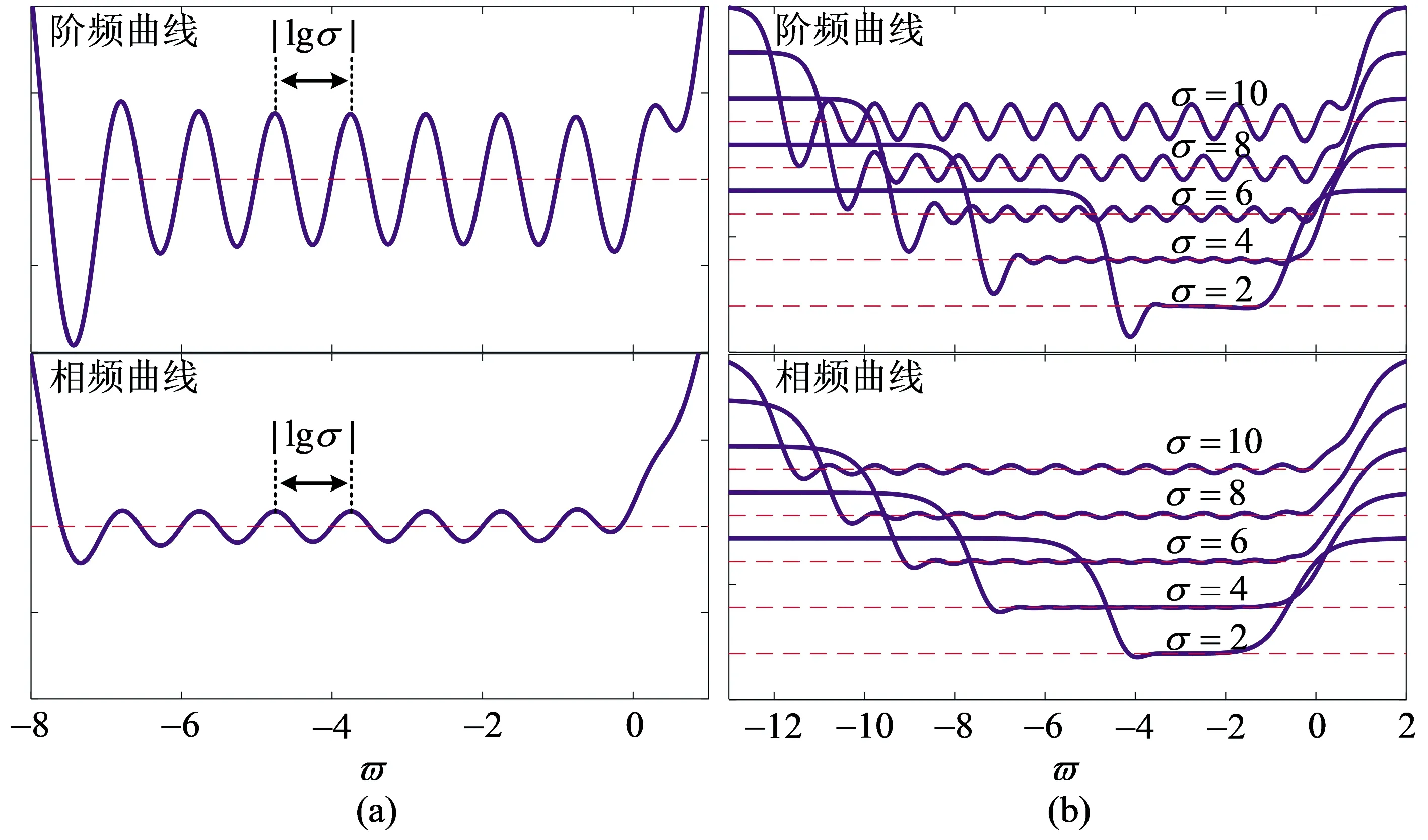
图8 优化标度分形塔分抗的运算特征曲线的振荡现象

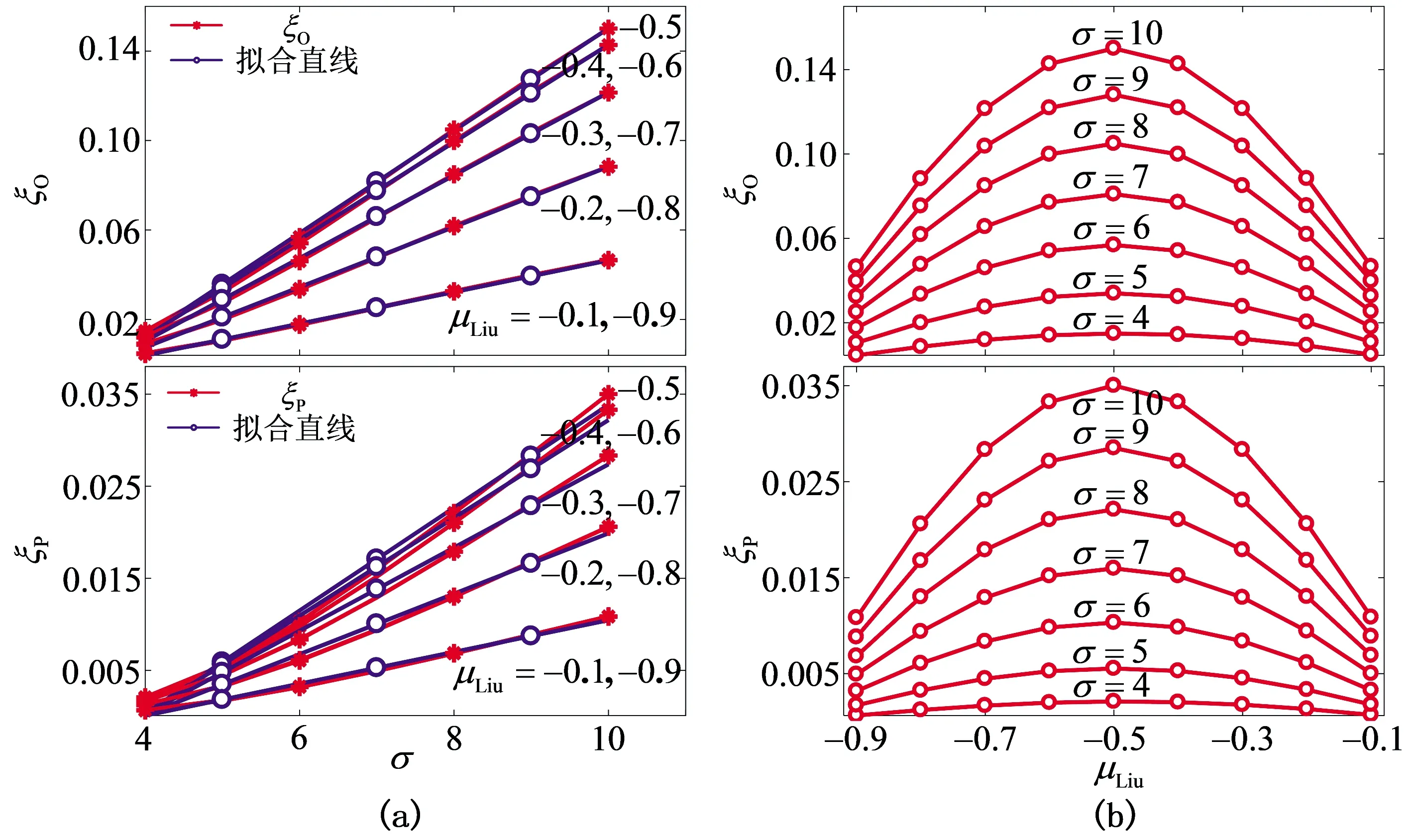
图9 振荡幅度与标度因子和运算阶的关系

当标度因子一定时，运算阶为μLiu(-1<μLiu<0)时振荡幅度与-1-μLiu时相等(图9(b)). 振荡幅度关于μLiu=-0.5对称分布. 已知频域振荡曲线的振荡周期W和振荡幅度(18)，阶频振荡曲线与相频振荡振荡曲线可表示为

μk(ϖ)≈μLiu+ξO(μLiu,σ)·

(20)

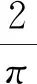
(21)

式中，初相位φO(μLiu,σ)，φP(μLiu,σ)的取值可由数值仿真精确求解. 当标度因子σ的取值小于4时，负半阶标度分形塔分抗的阶频特征曲线的振荡幅度小于0.012 8，相频特征曲线的振荡幅度小于3.363 5×10-4. 阶频和相频特征曲线在一个周期内的积分为

(22)

(23)

运算特征曲线的积分特性表明，尽管式(15)是阻抗函数在特定极限频率条件下的近似取值，但该计算结果同时表示逼近频带内运算阶的平均值[4].

图10 振荡幅度函数表达式中的参数

(a) slopeK；(b) interceptb

在研究分抗逼近性能的相关问题时，通常需要考虑相对误差函数和4种逼近精度取值[4].

阶频相对误差函数：

(24)

相频相对误差函数：

(25)

逼近精度ri：

r0=1%;r1=5%;r2=10%;r3=20%

(26)

优化前后的电路复杂度与迭代次数的关系分别为

ζσ[k]=2k+1-2

(27a)

ζσ-O[k]=2k+1-2+2=2k+1

(27b)

μLiu=-0.5时，由图7和图8可得标度分形塔分抗优化前后的逼近带宽指数为

πσ[k]=πσ-O[k]≈(k-1)·|lgσ|

(28)

由此可求出优化前后的逼近效益——逼近带宽指数与电路复杂度之比

(29a)

(29b)

式(29)表明当k取值较大时，负半阶标度分形塔分抗优化前后的逼近效益近似相等. 因为当μLiu=-0.5时，标度分形塔分抗的运算特征曲线能够较好地逼近理想分抗.μLiu≠-0.5时，该分抗逼近电路有待优化.

μLiu≠-0.5时，由图4(b)可知，优化前的逼近带宽指数为

πσ[k]≈[k-κ(μLiu)]·|lgσ|

(30)

κ(μLiu)是由μLiu确定的正实数. 优化后，以正比拓展不同运算阶μLiu下的阶频特征曲线为例，根据图11可知逼近带宽指数.

πσ-O[k]≥(k-4)·|lgσ|

(31)

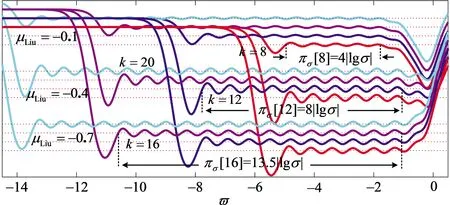
图11 正比拓展时阶频曲线的逼近带宽指数：σ=5Fig.11 The approximate frequency bandwidth exponent of order-frequency curves in direct proportion extension：σ=5

此时求出的优化前后标度分形塔分抗的逼近效益为

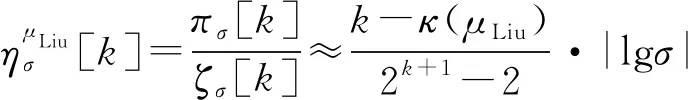
(32a)

(32b)

显然κ(μLiu)>4，即μLiu≠-0.5时，优化后的标度分形塔分抗逼近效益值明显大于优化前.

5 优化标度分形塔分抗电路的实现与运算阶扩展

5.1 电路设计与仿真

当标度因子σ一定时，运算阶为μLiu(-0.5<μLiu<0)时运算特征曲线的振荡幅度与运算阶为-1-μLiu时的相同(图9(b)). 当-0.5<μLiu<0时，振荡幅度随运算阶μLiu的增大而减小. 因此，可先分析-0.5<μLiu<0的情形.

在实际的工程应用中，往往需要在指定频段内运算有效的分抗元[1]. 对于给定的逼近带宽，若要降低分抗的电路复杂度，减少电路规模和设计成本，必须考虑合适的标度特征参量取值[2]. 尤其在给定逼近精度的条件下，标度因子σ太大将无法满足实际需求. 由式(20), 式(21), 式(24) 和式(25)知，标度因子的取值必须满足条件.

(33a)

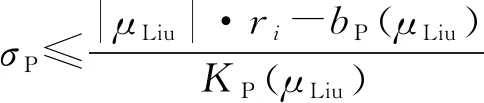
(33b)

该不等式可由式(34)等价变换得到.

(34)

当-0.5<μLiu<0时，根据式(15)、式(33)，可求出不同逼近精度下给定运算阶时，标度特征参量对数lgαO，lgαP的最大取值. 数值拟合得到的函数关系为

r0:lgαO≈-0.6536·μLiu-0.0291,

lgαP≈-0.9213·μLiu-0.0766

(35a)

r1:lgαO≈-0.9456·μLiu-0.0939,

lgαP≈-1.4314·μLiu-0.1646

(35b)

r2:lgαO≈-1.1599·μLiu-0.1328,

lgαP≈-1.7100·μLiu-0.1958

(35c)

r3:lgαO≈-1.4156·μLiu-0.1702,

lgαP≈-2.0027·μLiu-0.2174

(35d)

当-1<μLiu<-0.5时，α的取值同样可由式(35)确定，此时(35)式中的μLiu需替换为-1-μLiu. 优化标度分形塔分抗逼近电路的应用设计步骤如下.

(1) 由工程需求选择运算阶μLiu.

(2) 根据实际问题中逼近精度要求，由式(35)计算标度特征参量α；或根据振荡幅度要求，由式(33)计算标度因子σ，然后由式(15)求解标度特征参量α，β.

(3) 由工程应用中工作频段要求，计算逼近带宽. 根据公式(31)计算优化标度分形塔分抗的电路级数k.

(4) 根据特定电路的频率下限和阻抗范围，确定R和C的取值.

(5) 根据α，β，R和C的取值，设计优化标度分形塔分抗逼近电路.

由上述步骤，以μLiu=-0.2,-0.5,-0.7为例，根据逼近带宽和逼近精度等条件参数计算电路参数，设计实际优化标度分形塔分抗逼近电路. 条件参数及计算参数如表2.

Multisim14中仿真的幅频特征曲线和相频特征曲线(如图12)表明，设计的优化标度分形塔分抗逼近电路可逼近具有目标运算阶的理想分抗.

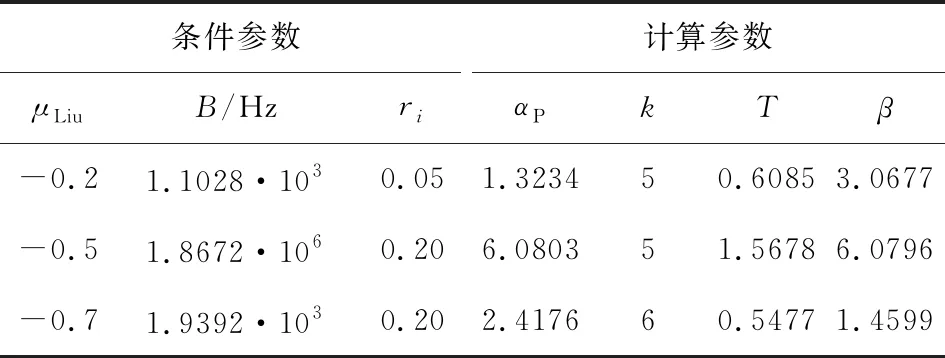
表2 标度分形塔分抗逼近电路设计参数表

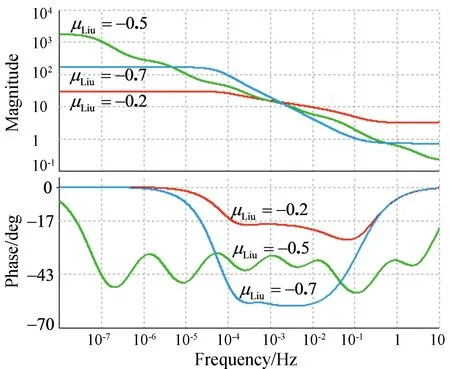
图12 不同运算阶的频域仿真曲线

5.2 运算阶的扩展

以上讨论的标度分形塔分抗都是容性分抗且运算阶-1<μLiu<0. 结合通用阻抗转换器[20-24]，使用电阻，电容和优化标度分形塔分抗构成有源电路网络，便可实现运算阶为-2<μLiu<-1的容性分抗及0<μLiu<2的感性分抗. 通用阻抗转换器的典型电路和等效阻抗表达式为

(36)

A，B为理想运算放大器. 当Z5为μLiu阶优化标度分形塔分抗，Z3为电容时便可构成(μLiu-1)阶分抗. 将Z4替换为优化标度分形塔分抗，能够实现(-μLiu)阶分抗. 若将Z2替换为电容，Z4为优化标度分形塔分抗可实现(1-μLiu)阶分抗. 以运算阶为μLiu=-0.2,-0.5,-0.7的优化标度分形塔分抗为基础，设计运算阶为-2<μLiu<2的分抗. 设计参数如表3和表4.

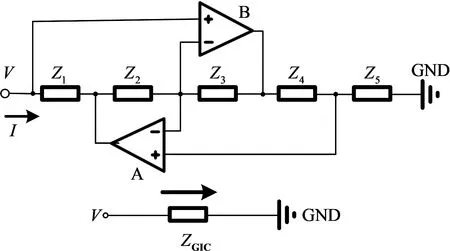
图13 接地通用阻抗转换器(GIC)典型电路

模拟电路的频域仿真曲线(如图14)表明，以优化标度分形塔分抗为基础，结合通用阻抗转换器设计感性分抗的方法是有效的，该方法克服了实际电路设计中电感不易集成等问题.

表3 运算阶为-2<μLiu<-1的设计参数

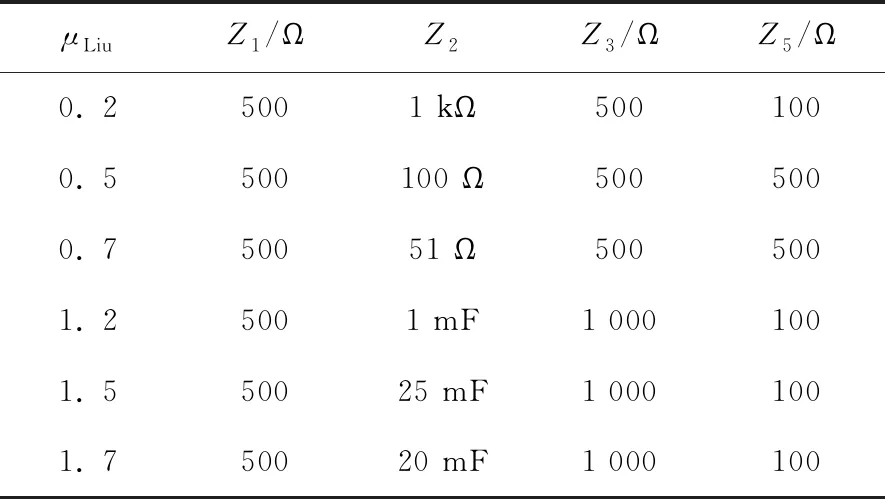
表4 运算阶为0<μLiu<2的设计参数

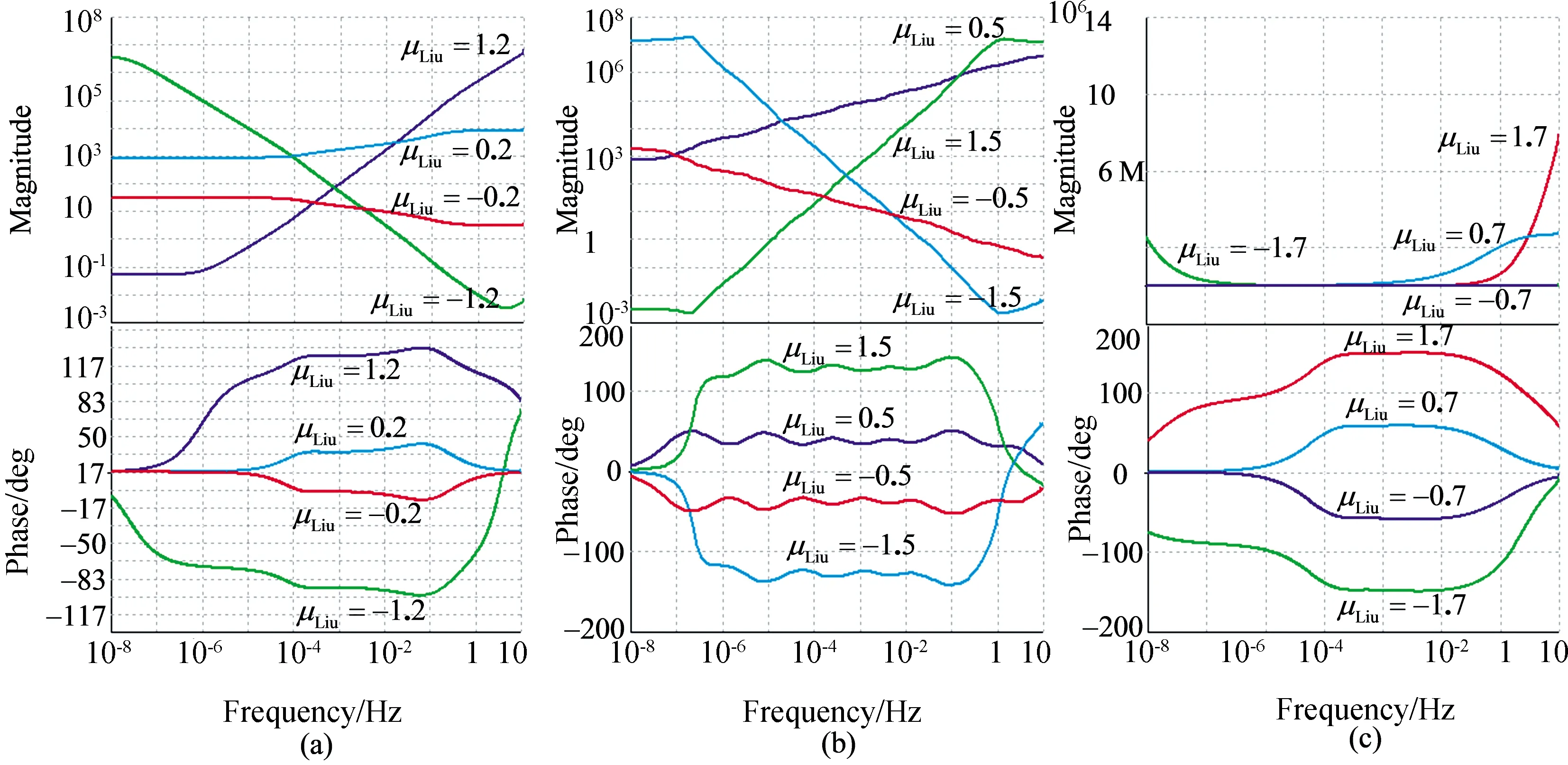
图14 不同运算阶的频域仿真曲线图：-2<μLiu<2Fig.14 Frequency-domain simulation curves of different operational orders-2<μLiu<2

6 结 论

标度拓展B型分形塔分抗逼近电路，获得具有任意分数阶运算性能的标度分形塔分抗逼近电路，并由双重标度方程(6)式描述. 根据(16)式选择合适的标度特征参量α、β能够设计任意阶分抗逼近电路. 定量分析标度拓展后的频域振荡波形并给出振荡模型函数. 根据标度因子取值，结合频域曲线的形状特征及电阻电容的电气响应特性，理论分析标度分形塔分抗逼近电路的优化方法. 对比分析优化前后分抗的逼近性能. 由于电感不适宜集成，提出不使用电感的条件下将优化标度分形塔分抗的运算阶由-1<μLiu<0推广到0<|μLiu|<2的设计方法0<|μ|<2. 由实际工程需求介绍优化标度分形塔分抗实际应用设计方案并给出实例. 理论和实验证明，本文提出的标度分形塔分抗的优化方法可行，优化标度分形塔分抗具有优良的应用价值.

标度分形塔分抗只是分抗逼近电路的一种，关于该分抗电路的优化还有如下需深入研究的问题：

(1) 是否存在优于本文的标度分形塔优化方法及优化元件参数值.

(2) 其他标度分形分抗电路同样存在频域曲线优化问题.

(3) 本文提出的优化方法是否具有普适性. 其他如四类Liu-Kaplan分形链分抗，标度分形格分抗等具有与标度分形塔分抗类似的频域曲线形状特征，本文的对称T型节是否同样可用于这些分抗的优化.

(4) 如何解析求解非正则标度方程(6). 如果能够获得该非正则标度方程解的解析表达式，或许可从数学解析的角度探讨电路优化方法及优化参数.