高精度多冗余捷联惯组配置优化设计与应用研究

2019-12-11申亮亮邵会兵管延伟谢劲励

导航定位与授时 2019年6期

王彬，申亮亮，邵会兵，管延伟，谢劲励

(1. 北京控制与电子技术研究所，北京 100038；2. 湖南航天机电设备与特种材料研究所，长沙 410205)

0 引言

惯性导航系统依靠自身的惯性器件完成导航任务，无需依赖任何的外界信息，也不向外辐射任何能量，具有短时精度高、自主性强、信息连续性好等优点，是一种应用广泛的导航系统。惯性导航系统主要是为飞行器提供一种惯性参考坐标系并测量视加速度及飞行姿态角，它的性能指标好坏直接关系到飞行器系统的制导精度[1-4]。惯性导航系统大致经历了平台惯性导航系统(Platform Inertial Navigation System，PINS)和捷联惯性导航系统(Strapdown Inertial Navigation System，SINS)2个发展阶段。与平台惯性导航系统相比，由于捷联惯性导航系统省去了硬件平台，因此系统部件少、结构简单，实现了惯性导航系统体积、质量、成本、可靠性方面的突破，具有广泛的应用前景。

随着对惯性传感器精度和可靠性要求的日益提高，以及组合导航技术的发展，远程飞行器对捷联惯性导航系统的精度和可靠性的要求也越来越高。提高捷联惯性导航系统的精度和可靠性一般可采用以下两种方法：1)提高陀螺仪或加速度计等单个惯性器件的可靠性，以降低故障的发生率；2)增加一定数量的陀螺仪和加速度计，即通过冗余增加部组件的故障容许次数。在实际应用中，单个惯性器件性能提升要通过大幅提高加工工艺水平从而提高惯性器件的精度，难度太大。由于控制理论和计算机技术的发展，采用冗余配置技术提高导航系统的可靠性和精度已成为惯性导航技术的发展方向和国内外研究热点之一[5-14]，多冗余捷联惯组可以根据系统需求，灵活地实现惯性器件的冗余配置，分担指标实现难度，有效提高系统的精度和可靠性。捷联惯组的冗余配置大致分为两种[11-14]：测量轴的正交配置方案和非正交配置方案。多冗余捷联惯组配置优化设计一般是在惯性器件个数确定的前提下进行的。采用非正交配置时，目前比较经典的非正交配置方案，如6个惯性器件组成的冗余系统，其测量轴分别沿十二面体的6个平面的法线方向配置，精度分配比较平均，但需要对加速度计陀螺仪的输出进行附加计算，以得到沿载体主轴的测量信息，不仅增加了飞行控制计算机的计算量，且会引起新的计算误差；采取正交配置时，惯性器件直接输出载体主轴的测量信息，无需计算，且正交配置方案更有利于提高某特定方向的测量精度，计算误差小，制造难度低，实时性好。

本文针对远程飞行器使用需求，研究了一种高精度多冗余捷联惯组配置优化设计与应用方案，通过高精度多冗余捷联惯组配置优化设计，采用导航信息一致性检测及融合技术，实现了高精度多冗余捷联惯组高可靠、高精度应用。

1 多冗余捷联惯组配置优化研究

通过制导精度分析，对远程飞行器采用的多冗余捷联惯组主要技术指标进行分配，以满足制导精度的要求。综合考虑系统可靠性需求、产品体积质量及实现的复杂度、系统应用算法难度，选择冗余配置方案。通过配置多只高精度加速度计和陀螺仪，在提高可靠性的同时保证了相应测量通道的稳定性，通过器件可用性筛选确保冗余后精度的提高。

1.1 多冗余配置方案

冗余惯性器件数量增加后，系统精度和可靠性将得到提高。但并非冗余惯性器件越多越好，因为在惯性器件数量增加的同时，系统的体积、质量和成本也相应增加，而可靠性和精度的增长却并不显著。因此进行惯组配置优化需要从系统使用需求、可实现性和可靠性等角度进行综合考虑。

根据远程飞行器复合导航分析结果可知，惯性导航系统各项误差对导航误差的影响程度不同，X向加速度测量通道(与飞行器载体坐标系X轴重合)的影响最大。因此，在飞行控制计算机性能有限和优先提高某个特定方向测量精度的场合，采用正交配置方案。冗余配置方案如图1和图2所示，考虑到陀螺仪的可靠性高，陀螺仪采用6表正交配置方案，每个方向2只陀螺仪。加速度计采用9表冗余配置方案，其中Ax测量通道配置4只加速度计，充分保证X向加速度测量通道的稳定性，提升测量精度；Ay和Az通道分别配置2只加速度计；第9只加速度计配置在YOZ平面与Y轴成45°夹角，主要用于对Y、Z向加速度输出进行故障检测，提升加速度测量通道的可靠性。在冗余配置基础上，多冗余捷联惯组还通过惯性器件可用性筛选确保冗余后精度的提高。

图1 陀螺仪冗余配置方案Fig.1 The redundant configuration of gyroscopes

图2 加速度计冗余配置方案Fig.2 The redundant configuration of accelerometers

1.2 冗余配置可靠性分析

对于惯性器件，可以认为故障次数为随机变量，而单位时间内发生故障的次数很小，同时在一段时间间隔t内发生故障的次数在一个有限的平均值附近摆动，此时在时间间隔t中恰好发生x次故障的概率可近似用泊松分布来表示[15-16]

(1)

式中，λ表示单位时间内发生故障的次数；令T=λt表示时间t内发生故障的平均次数，称其为归一化时间。设x=0，则有

p(0)=e-λt

(2)

式(2)表示在单位时间t内一次故障也没有发生的概率，通常称为该惯性器件的可靠性函数，即器件可靠度为

R(t)=e-λt

(3)

则该器件的平均无故障时间为

(4)

图3 无冗余捷联惯组可靠性逻辑框图Fig.3 The reliability logic diagram of Non-RIMU

对本方案，设6个陀螺仪具有相同的可靠度Re1，即

R1(t)=R2(t)=R3(t)=R4(t)=R5(t)=R6(t)=Re1=e-λ1t

(5)

陀螺仪可靠性逻辑框图如图4所示，系统能正常完成角速度测量工作的可靠度Ra1(t)为

(6)

图4 冗余惯组陀螺组件可靠性逻辑框图Fig.4 The reliability logic diagram of gyroscopes in RIMU

加速度计可靠性逻辑框图如图5所示，若9只加速度计具有相同的可靠度Re2，系统能正常完成加速度测量正常工作的可靠度Ra2(t)为

Ra2(t)=[1-(1-Re2)4]·{1-(1-Re2)[1-

(1-(1-Re2)2)2]}

(7)

图5 冗余惯组加速度计组件可靠性逻辑框图Fig.5 The reliability logic diagram of accelerometers in RIMU

则系统能正常完成测量的可靠度Ra(t)为

Ra(t)=Ra1(t)·Ra2(t)

(8)

假设Re1=0.992，Re2=0.995，无冗余捷联惯组能正常完成测量的可靠度为

(9)

而本配置方案系统能正常完成测量的可靠度为

Ra(t)=Ra1(t)Ra2(t)=0.99975802

(10)

可见，本配置方案系统测量可靠度有显著提升。

2 多冗余捷联惯组信息一致性检测及融合研究

2.1 惯组信息一致性检验

多冗余捷联惯组数据融合是将多个同类惯性器件的信息进行融合处理，精度相比单一惯性器件有了进一步的提高[10, 16]，其融合前必须进行一致性检测。采用置信距离测度一致性检验方法，在惯性器件测量模型的基础上，建立惯性器件关系矩阵，剔除误差较大或失效的惯性测量信息[17-18]。

多惯性器件测量同一参数时，假设第i个和第j个惯性器件测量值分别为Xi和Xj，二者均服从正态分布，以其概率密度分布函数作为惯性器件的特征函数，记成pi(x)和pj(x)，xi和xj分别为Xi和Xj的一次观测值，置信距离测度一致性检验法介绍如下：

为反映xi和xj之间的偏差，引进置信距离测度的概念，设

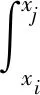
(11)

(12)

dij称为第i个惯性器件与第j个惯性器件数值的置信距离测度，dij值越小，2个惯性器件的观测值越接近，否则偏差就越大，因此也称为融合度；同时dij也可借助于误差函数erf直接求得

(13)

若对于n个惯性器件的测量数据，根据试验结果给出dij和阈值αij，构成多冗余惯性器件的置信距离矩阵Dn为

(14)

(15)

当rij=0，则认为第i个惯性器件和第j个惯性器件相融性差，或称它们互相不支持；若rij=1，则认为第i个惯性器件和第j个惯性器件相融性好，称第i个惯性器件是支持第j个惯性器件的；若rij=rji=1，则称第i个和第j个惯性器件相互支持。如果一个惯性器件不被一组惯性器件所支持，或只被少数惯性器件所支持，则这个惯性器件的输出是无效的，应剔除掉此惯性器件。多冗余惯性器件测量同一参数时，所有有效数据的集合称为融合集，经过对置信距离测度一致性检验法的分析可知，该方法原理含义清晰，判断准确而高效。

2.2 惯组信息融合

完成多冗余捷联惯组信息一致性检验后，即可对信息进行融合。多冗余捷联惯组将6只陀螺仪和9只加速度计冗余配置成4组惯性测量单元(Inertial Measurement Unit, IMU)的方案，需要进行4组虚拟IMU数据标定计算，分组情况如下：

1组：Ax1，Ay1，Az1，Gx1，Gy1，Gz1；

2组：Ax2，Ay2，Az2，Gx2，Gy2，Gz2；

3组：Ax3，Ay1，Az1，Gx1，Gy1，Gz1；

4组：Ax4，Ay2，Az2，Gx2，Gy2，Gz2。

其中，YOZ平面内的斜置加速度计AD仅用于故障检测，不参与惯性导航计算。

进行4组标定解算后，4组标定结果中惯性器件安装误差分别基于不同的IMU坐标系确定，给误差补偿、数据融合和斜置器件标定带来一定困难，需要将4组IMU坐标系统一到本体坐标系。即在各组IMU完成系统标定后，定义第1组IMU坐标系为惯组的本体坐标系，将其他3组IMU坐标系通过坐标转换到本体坐标系。

统一坐标系后，在导航过程中对各个惯性器件的输出信息进行信息融合,计算如下

(16)

其中，ωAxi、ωAyi、ωAzi、ωGxi、ωGyi、ωGzi为信息融合权值，实际使用中可采用加权信息融合方案或平均信息融合方案。

3 仿真实验与结果分析

3.1 惯组一致性检验方法分析

在静态条件下采集多冗余捷联惯组输出，在100～120s向Ax4加速度计增加10mg的常值零偏，测试数据如图6所示。据此对X向4只加速度计输出进行一致性检测分析。

图6 静态条件下X向加速度计输出Fig.6 The output of X accelerometers under static condition

利用置信距离测度一致性检验方法进行分析。根据实际经验，取阈值αij=0.7，通过上面的公式计算关系矩阵Rn。

从数据分析结果可以看出，100s之前系统的关系矩阵Rn为

在100～120s，系统的关系矩阵Rn为

从关系矩阵中可以看出，在120s后，Ax1、Ax2、Ax3号加速度计都不支持Ax4，Ax1、Ax2、Ax3加速度计都相互支持。因此，此时Ax4加速度测量信息不准，应当剔除。

分析结果验证了一致性检测方案的正确性和有效性，且该方案计算简单，能简便快速地定位故障通道，并剔除不良测量信息，适用于多冗余捷联惯组信息融合前的数据预处理和一致性检测。

3.2 惯组信息融合性能分析

结合远程飞行器飞行基本过程设定飞行轨迹，飞行时间0.5h，飞行轨迹在水平面和垂直面的投影分别如图7和图8所示。

图7 飞行轨迹在水平面的投影Fig.7 The horizontal projection of flight path

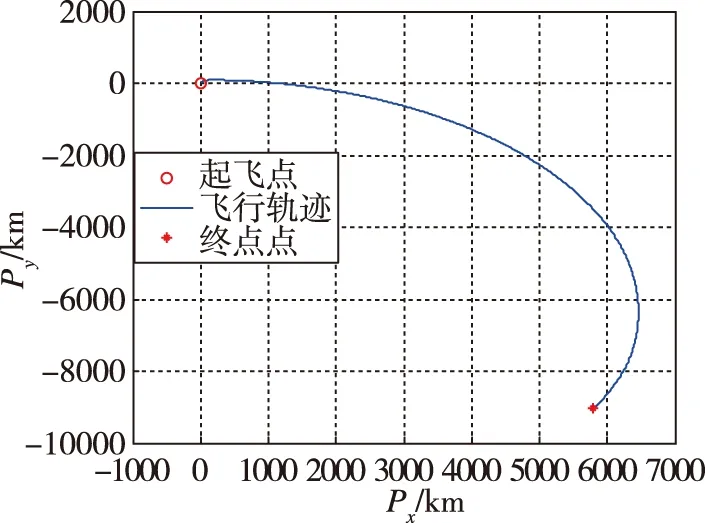
图8 飞行轨迹在垂直面的投影Fig.8 The vertical projection of flight path

根据制导系统方案设定加速度计和陀螺仪误差参数。在飞行过程中，多冗余捷联惯组和传统无冗余捷联惯组的惯性导航误差对比如图9所示。

由图9可以看出，多冗余捷联惯组的惯性导航精度显著优于传统无冗余捷联惯组。无冗余捷联惯组导航误差1530m，多冗余捷联惯组导航误差790m，多冗余捷联惯组的惯性导航精度提升近1倍。远程飞行器的惯性导航性能主要受X向加速度测量通道影响，多冗余捷联惯组通过冗余配置显著提高了X向加速度测量通道的测量精度，满足了远程飞行器的高精度使用需求。

图9 远程飞行器的惯性导航位置误差Fig.9 The inertial navigation position errors of LRA

采集多冗余捷联惯组长时间(6h)静态数据(惯组X-Y-Z轴近似指向北-天-东方向)，对其进行百秒方差统计，结果如表1所示。由表1可以看出，通过数据融合，角速度测量通道离散度减小，数据稳定性得到提高。AX、AY向加速度测量通道通过数据融合后的离散度略差于最好的通道。数据处理结果表明，通过冗余配置与信息融合，角速度测量通道稳定性优于0.01(°)/h(3σ)，加速度测量通道稳定性优于1×10-5g(3σ)。

表1 百秒方差统计结果(3σ)

利用长航时静态数据进行惯性导航计算，结果如图10和图11所示(第1～4组的导航误差有正有负，为便于对比分析，将导航东向误差均以负值画出、导航方位误差均以正值画出)。可以看出，信息融合后的位置和姿态导航误差均显著减小，进一步表明了惯性器件的信息融合可以提升相应测量通道的稳定性，抑制惯性导航误差的发散；同时通过信息融合前的一致性检测还可以及时定位和隔离故障信息，提高系统的可靠性，使多冗余捷联惯组的整体性能显著提升。