触摸概念的本质

张平

【摘   要】平均数作为一个统计概念，在统计学中具有极其重要的地位。以往的教学更偏重于对平均数的计算，忽视了对平均数概念本质的认识。而基于数学史的平均数教学，力求还原平均数的本原意义，教学中以估计大数作为认知的起点，在问题解决和不断质疑中深化对平均数本质的认识，从而指向概念的本质。

【关键词】平均数;数学史;教学设计;问题解决;概念

平均数作为一个统计概念，在统计学中具有极其重要的地位。以往的平均数教学大都将教学重心放在解决问题层面上，更注重训练学生平均数的计算技能。然而，在新课程标准中，“统计与概率”作为一大领域出现，[1]并且随着信息技术的不断发展以及“云技术”“大数据”的不断涌现，学会数据分析和用数据说话，已经成为每一个公民必备的数学素养和思维方式。在此背景下，平均数作为一个重要统计量的身份越来越被重视。与此同时，一些教师也已对平均数意义的教学做了很多有益的探索，但仍有一些不足。譬如，如何在数据分析的背景下促使学生理解平均数的意义，平均数的本质究竟有哪些，等等。鉴于此，本文试着从平均数发展历史的角度，尝试解决上述平均数教学中的一些问题，以期为这一内容的教学提供一些参考。

一、平均数的发展历程

M.克莱因说：“数学史是教学的指南。”[2]纵观平均数的发展史，可见其极其丰富而又深刻的内涵。正如一位学者所说的那样，如果我们从理论的角度走一点极端，则可以说，一部数理统计学的历史，就是从纵横两个方向对算术平均数进行不断深入研究的历史。[3]纵观平均数的发展历程，大致包括以下几个方面（见表1）。

表1   平均数的发展历程

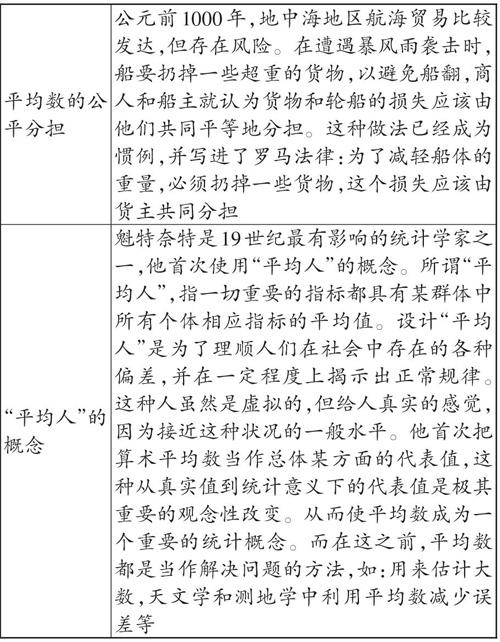
[阶段 主要历史事件 利用平均数估计大数 历史上平均数的意义最早是用来估计较大数：4世纪，印度鲁帕那（Rtuparna）为了估计果树上树叶和果实的数目，选取一根枝条，数一数上面的叶子和果实的数量，再乘枝条数，这样就可以估計出整棵树的叶子和果实了 重复测量取平均数以减少误差 16世纪末，第谷（Tycho Brahe）为了减少观测的误差，率先取重复测量值的平均数作为天文学观测的数据，有效地减少了系统误差 平均数的补偿性 [古希腊时期，数的大小用线段表示（如下图所示），其平均数的定义是：a和c中间的数b称为算术平均数，当且仅当b-a=c-b。图中最长的线段长度为10，最短的线段长度为2，中间线段的长度为6，这种方法直观地显示了平均数介于两个极值之间，给补偿策略求平均数很好的启示。]

值得一提的是，中国《九章算术》“方田章”也有关于平均数算法的描述：

今有三分之一，三分之二，四分之三。问：减多益少，各几何而平？答曰：减四分之三者二，三分之二者一，并以益三分之一，而各平于十二分之七。

题中采用“平分法”来求解 。平分指当各个分数不相等时，为使它们相等，可减去那个分数多的部分，增补这个分数少的部分，这实质就是移多补少的方法 平均数的公平分担 公元前1000年，地中海地区航海贸易比较发达，但存在风险。在遭遇暴风雨袭击时，船要扔掉一些超重的货物，以避免船翻，商人和船主就认为货物和轮船的损失应该由他们共同平等地分担。这种做法已经成为惯例，并写进了罗马法律：为了减轻船体的重量，必须扔掉一些货物，这个损失应该由货主共同分担 “平均人”的概念 魁特奈特是19世纪最有影响的统计学家之一，他首次使用“平均人”的概念。所谓“平均人”，指一切重要的指标都具有某群体中所有个体相应指标的平均值。设计“平均人”是为了理顺人们在社会中存在的各种偏差，并在一定程度上揭示出正常规律。这种人虽然是虚拟的，但给人真实的感觉，因为接近这种状况的一般水平。他首次把算术平均数当作总体某方面的代表值，这种从真实值到统计意义下的代表值是极其重要的观念性改变。从而使平均数成为一个重要的统计概念。而在这之前，平均数都是当作解决问题的方法，如：用来估计大数，天文学和测地学中利用平均数减少误差等 ]

二、平均数的内涵及其教学分析

学生学习平均数，关键是要理解其本质。就数学概念而言，理解其本质可以从多个层面入手，如逻辑关系、数学史的发展和教育心理学等。每个层面对于理解概念都会有不同的帮助。对于数学史而言，追溯一个概念的形成历程，往往可以发现其“本来面目”，从而为理解其本质和组织教学带来有益的启示。

（一）平均数的内涵

通过平均数的发展历程我们可以看到，平均数丰富而又深刻的统计意义是在各个发展阶段逐步形成的。其主要特征有：平均数是被平均的数据的代表;平均数介于最小值和最大值之间;平均数易受到不等于平均数的数据影响;平均数不一定是数据中的一个值;平均数可能是一个在现实意义中不存在的数;计算平均数，要考虑数值为零的数据在内。除此之外，平均数的统计意义主要包括：作为判断事物的数量标准或参考。例如，评价某个学生的身高情况，通常可以将这个学生的身高同这个地区同年龄同类型学生的平均身高进行比较;作为代表来比较不同总体之间的水平，如比较人数不相同的两组学生投篮的水平。人数相同，则可以比较总数，人数不同，则可以用平均水平来比较;作为用样本的平均数来推断总体的水平。在统计估计中，往往是根据样本的平均数来推测总体的平均数;作为总体的平均数通过在某段时间内的发展变化，探索研究对象的发展规律。

与此同时，在平均数教学时，还必须厘清平均数与中位数、众数的关系 。在统计学中，平均数、中位数、众数都是反映一组数据的集中趋势的统计量（具体关系可参见图1）。当统计数据符合或者接近正态分布时，三者是基本一样的，如果数据偏态分布，三者才会有区别。因此用三个中的哪一个来表示一般水平，需要看数据的情况。

图1 平均数、中位数和众数的关系

（二）平均数的教学分析

荷兰学者A.Bakker曾做过专门研究，他发现学生对平均数的理解与历史有相似之处。他通过分析历史与个体学习过程之间的相似处与不同点，从众多统计学历史资料中甄选出有价值的材料用于教学，并发展了一套帮助学生学习平均数的教学方案，其基于平均数历史的教学建议包括：估计大数是一种古老的统计方法，可以作为学生学习平均数的认知起点;学生可能会使用中点值作为求平均数的原始方法;利用条形图表征数据能帮助学生使用补偿策略来估计平均数。[4]

比较目前四种版本的小学数学教材（人教版、苏教版、北师大版、青岛版）发现，对于平均数内容的编排，也借鉴了以上的一些研究成果，如比较重视条形统计图来帮助学生实施移多补少的策略。在平均数的引入方面，四种版本的教材不约而同地采用了个数不同的两组数据进行比较。当两组数据不能用总数来比较时，需要寻求新的分析方法来解决问题。这样导入的好处就是能直接引起学生的认知冲突。但问题是学生可能不能深入理解平均数作为一组数据的代表。用平均数来估计大数，其核心思想就是在许多数据中找一个表示一般水平的代表。平均数的起源中数树叶的故事，其方法就是找到一根属于一般水平的枝条代表，从而估计出整棵树的树叶数。平均数作为一组数据一般水平的代表，应该是平均数性质中最核心的。基于此，把估计总数作为认识平均数的起点是合适的。可以看出，平均数的公平分享起源与人们直觉中的公平、公正、平等是相互联系的，这就意味着公平分享的背景有助于学生理解平均数的意义。

三、基于平均数发展史的教学设计

用平均数历史来指导教学，关键要思考两个问题：一是平均数核心的内涵主要有哪些;二是如何设计一系列能够触及平均数意义和本质的问题，让学生在解决问题的过程中把握平均数内涵，感悟平均数所蕴含的数据分析观念。根据以上分析，笔者在设计平均数的意义时，把平均数的发展历史作为教学的指南，力求让学生经历创造平均数的历程。具体过程如下。

（一）用估计总数作为认识平均数的起点

首先，笔者创设了学生熟知的做操的情境。操场上的10列学生，每一列人数不同（如图2所示）。

图2   学生做操队列的人数

笔者让学生不通过计算，用自己喜欢的方法来估计做操的人数。经过交流，有学生认为人数在40与90人之间，因为最多一列人数是9人，最少一列人数是4人;也有学生说是60人左右，因为大多数的列是6人，少数列比6人多，还有少数列比6人少，所以把每一列都看作6人。这个方法得到了一致认可。从学生发表的几种意见中，我们可以看到学生凭借其原有的生活经验和认知水平，敏锐地发现了这组数据中的典型数据，它可以作为这些数据中的每一个数据的代表，从而迅速估计出做操人数。学生在经历这样的过程中实际已经初步构建出平均数的雏形：数据的代表。这样设计实际可以达到两个目的，一是唤醒，学生的潜意识中都有均等意识，尽量使每一列人数一样多是学生原有经验，设计中通过估计人数让学生利用这个经验来解决实际问题，从而达到唤醒和强化的作用;二是铺垫，寻找数据的代表，不仅能解决估计大数的问题，还能解决后面比较两组数据的实际问题，这也是为经验的迁移做准备。

（二）在实际问题中还原平均数的本原意义

在这一个层次的教学中，笔者利用学生套圈游戏的情境，分四个小组对套中的情况进行分析。每一个小组情况的分析实质都蕴含了平均数的不同层次的性质。

第一小组                                 第二小组

图3   第一、二小组学生套圈个数的条形图

实际教学中，在比较第一小组和第二小组哪组套得准一些时，学生原有的比总数的经验还是有明显的负迁移的作用。笔者在这里放手让学生进行比较，通过思维的激烈碰撞，学生终于意识到在人数不同的情况下，采用比较总数的方法是不公平的，转而寻找其他方法。学生发现可以找两组数据的代表，前面的经验在这里得到了很好的迁移。由于条形图的直观性，学生容易发现通过移多补少就能找到一组数据的代表。当然也有水平更高的学生直接通过计算得到。在这个教学设计中，没有突出平均数的计算方法，而是在不断的认知冲突中，在对两组数据充分比较分析中寻求解决问题的办法，是真正让学生在用数据说话的過程中完整而又深刻地理解平均数的意义。

表2   第三小组男生套中个数表

[姓名 王欣 李小林 金智杨 张宇 钱一涛 套中个数 6 5 5 5 4 ]

表3   第三小组女生套中个数表

[姓名 李小虹 王丽 赵霞 张圆圆 钱雅芸 套中个数 7 5 6 6 0 ]

计算第三小组男、女生套中的平均数（如表2、表3所示），男生平均套中个数很顺利就解决了，计算女生平均套中个数时，出现了两种不同意见，一种意见认为钱雅芸同学没有套中，不应该计算在内，另一种意见则反之。本来在设计前认为很容易解决的问题，但在实际教学中学生的争论比较激烈。不过，通过这样有质量的讨论和交流，学生对于平均数的这一条性质应该理解得比较透彻了。

第四小组情况分析分为两个层次，首先是告诉学生第四小组4个学生的平均成绩是5个，让学生估计每个学生套中的个数，这是一个比较开放的问题。通过交流，学生知道平均数5个不一定是每个同学都套中5个，有可能比5个多，也有可能比5个少。由此可见，学生很好地理解了平均数是介于最大数和最小数之间的。其次，告诉3个学生套中的个数，让学生想办法算出第4个学生套中的个数。

通过上述一系列问题情境的设置，教师不断地赋予平均数各种意义，使学生在认真分析一个个精心设计的数据时，通过对平均数算法的探索和对数据的观察分析，自主构建平均数的意义。

（三）在应用中深化对平均数的理解

一般而言，在一个数学概念初步建构形成表象以后，需要不断地在概念的应用中进一步抽象、概括、发展概念的内涵，[5]平均数的教学也不例外。在应用层次的教学中，笔者设计了某小学10岁儿童平均身高的实际问题（如图4所示）。

图4   某校2014年10岁男童身高情况

这样的设计实际上是把平均数放到一个更为广阔的视野里让学生来应用和理解其实质。围绕这个情境，笔者设计了如下问题：（1）请你估计学校10岁儿童的平均身高;（2）小明2014年正好10岁，他的身高是134厘米，请你分析小明的身高情况，你有什么建议？（3）你身边还有哪些平均数可以像平均身高一样用来比较？

关于第一个问题，学生都能够比较准确地估计出平均身高，散点图也能够直观地表达平均数是表示一组数据的集中趋势的意义。第二个问题实际是培养学生数据分析、判断和决策的能力。第三个问题是让学生意识到生活中平均数应用的广泛性，生活中离不开数据的分析和比较。这三个问题旨在让学生经历一次完整的数据整理、描述并做出判断分析的过程，而这正是统计学的基本思想。

（四）在质疑中进一步拓展平均数的内涵

学贵有疑，平均数概念的“疑”在何处？平均数是描述数据集中趋势的重要统计量，但数据的分布对其影响比较大，当数据偏态分布时，人们一般用中位数替代平均数。有时个别数据也会对平均数产生影响，当极端数据出现时，平均数代表的往往就不是一般水平了。认识平均数必须知道它的另一面，而这些也是平均数意义的一部分。

这一层次的教学，笔者设计了公司员工工资的问题，首先出现员工工资的数据，让学生估计他们的平均工资。其次让他们说说总经理的工资，并根据学生说的数据让他们画画平均数的位置，当总经理工资很高时，学生发现表示平均工资的那根线已经远远偏离了一般员工的工资。这时教师提问，如果以这样的平均工资数去招聘员工合适吗？学生马上就产生了激烈的争论，一部分认为这是公司的平均工资，没有欺骗，一部分学生认为这样应聘会上当受骗。再次，在学生的争论中，教师适时指出平均数有时也有缺陷，像这样的情况用平均数来表示公司员工工资的一般水平显然不合适。“疑”有何用？当一组数据用平均数表示不合适时，就需要用新的表示方法来表示了，这也是数学概念發展的一般规律。

如何才能让学生真正触及概念的本质，通过以上教学实践，笔者以为至少要具备两点，一是对于概念本身而言，它必须能够揭示概念最本质最原始的内涵。数学概念往往在经过动态演化的过程之后，凝聚成一个静态的结构，在某种程度上掩盖了深层次的同时又是作为数学核心的思想方法。比如在平均数的教学中，以前有的教师就简化为求平均数，忽略了平均数形成过程中丰富而又深刻的统计思想。二是对学生而言，要让学生自我建构，获得自我的意义。用弗赖登塔尔的话就是要把“冰冷的美丽化为火热的思考”。 [6]倘若如此，教学中就要设计能够让学生触及概念本质的问题，用问题驱动学生进行自我建构，在问题解决的过程中让学生获得本质的、朴素的数学思想和方法。

参考文献：

[1] 中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2] M·克莱因.古今数学思想[M].上海：上海科技出版社，1979.

[3] 陈希孺.数理统计学简史[M].长沙：湖南教育出版社，2002.

[4] BAKKER A.The Early History of Average Values and Implications for Education[J]. Journal of Statistics Education，2013，11（1）.

[5] 徐文彬.课堂教学中的“本原性问题”及其教育价值[J].当代教育科学，2004（19）：13-14.

[6] 弗赖登塔尔.数学教育再探——在中国的讲学[M].刘意竹，杨刚，译.上海：上海教育出版社，1999.

（江苏省张家港市崇真小学   215633）