从数学史中汲取小学数学核心素养的因子

2019-12-10钱利平邵汉民

教学月刊·小学数学 2019年11期

钱利平邵汉民

【摘要】数学不会离开数学史而凭空产生，数学核心素养需要落实在日常的数学教学之中。在明晰了小学数学史基本内涵、小学数学核心素养基本内涵的基础上，探究从数学史中汲取数学核心素养的因子的策略，能使数学史与数学教育构建起有机的联系。

【关键词】小学数学史;小学数学核心素养;内涵;联系

小学数学史是数学史的重要组成部分，在小学数学教材中，有专门的数学史料的介绍，也有部分融入教材编写之中。同时，数学史的教学价值越来越被专家与教师所重视，如华东师范大学的汪晓勤教授所带领的团队对数学史如何融入日常教学进行了长期的实践研究[1]，西南大学的宋乃庆教授则以数学史为素材进行小学数学拓展课程的开发[2]，等等。但是，我们也发现小学数学教师职前缺少相应的数学史的学习，在职后也不知道如何结合具体的课例寻找相应的数学史。小学数学核心素养是数学核心素养的重要组成部分，其内涵虽然还没有达成共识，但是《普通高中数学课程标准（2017年版）》中的数学核心素养以及小学数学教育专家对于小学数学核心素养的讨论都可以给我们理解小学数学核心素养以启示。在认识了“小学数学史”与“小学数学核心素养”内涵的基础上，依据两者的联系，可以从小学数学史中汲取小学数学核心素养的因子。

一、小学数学史的基本内涵

这里的小学数学史，是指小学数学教材中的数学知识的产生与形成的历史，以及由此形成的数学思想方法与数学精神。可以分成三个方面，第一个方面是数学知识的产生与形成过程，体现的是数学的历史性;第二个方面是数学思想方法，体现了数学的科学性;第三个方面是数学精神，渗透了数学史的教育性。

（一）体现数学的历史性

数学是研究数量关系与空间形式的科学。同时，这一研究过程并不是一蹴而就的，需要经历漫长的产生与形成的发展过程。数学史就是要真实地还原这一段段历史。

如对于长度的测量，在确定长度单位时，人们最先采用“以身为度”的方式，即用身体某一部分的长度作为单位来进行测量，如“庹”“拃”等。随着测量精度的增加与交流需要，逐步形成了国际单位，如米、分米、厘米等。人教版二年级上册《长度单位》例1就引用了“以身定度”的片段。因此，教师只有了解长度单位的形成历史，才能够理解教材的编写意图，并适时介绍“排黍定度”“子午定度”“光波定度”，让学生了解長度单位形成的历史。[3]

但是，基于数学史编写的教材例题非常罕见。对于一些数学概念、符号、法则等的产生与形成历史，教师要能够适当了解，并组织成数学教学环节。如字母表示数，人类经历了文字表示数、字母缩写表示特定的数到用字母表示一般的数，教师可以创设合理的教学情境，让学生经历这样的过程。[4]

（二）体会数学的科学性

数学思想方法是人们在研究数量关系与空间形式时的思维方式与操作规则。数学思想方法来源于数学知识，又高于数学知识，相对于数学知识的历史性，数学思想方法更体现出数学的科学性。

如圆周率的值，我们知道它是一个常数，且是一个无限不循环小数。但是，如何求得呢？人们经历了实验时期、几何时期、分析时期和计算机时期四个时期。推算圆周率的过程，就是不断升华数学思想、提炼数学方法的过程。[5]

因此，在学习数学知识的过程中，我们要不断地追问，在它的产生与形成过程中，包含着哪些思想方法，使“学数学”的过程成为“用数学学”的过程。

（三）渗透数学的教育性

有位教师在教学六年级数学拓展课“圆的魅力”时，向学生提问：“我们为什么能够在短短的几节课中学习了这么多有关圆的知识？”学生有的回答是由于自身的努力，有的回答是因为老师指导，等等。这时教师指出其实最重要的是感谢一类人——数学家。然后教师讲了“阿基米德之死”，并指出每一个数学符号、数学公式……的背后，都有着这样一个个感人的故事。[6]

确实，数学史记录的不仅仅是数学的知识与思想方法的历史，更记载着人类探究数学与应用数学的历程，其中，有许许多多的感人故事，值得我们作为教育资源进行开发，用生动的事例、巧妙的设计，再现数学知识的产生与形成的历史。

历史性是数学史区别于数学的基本特征，科学性是数学史需要评析与提炼的重要内容，教育性则是数学史所具有的人文特征，也是作为数学教育工作者需要特别关注的内容。

二、小学数学核心素养的基本内涵及数学史与其的关联性

小学数学核心素养的研究是当前小学数学课堂教学研究的热点之一，但对于它的基本内涵是什么还没有达成共识。

（一）小学数学核心素养的讨论

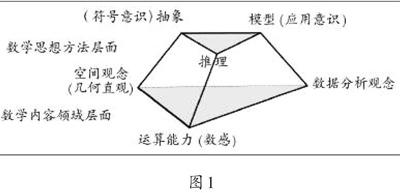
对于小学数学核心素养的讨论，有两种基本思路，第一种从《义务教育数学课程标准（2011年版）》的10个核心词进行概括，如曹培英老师把10个核心词中具有数学特色的9个分成数学思想方法层面与数学内容领域层面，构建起小学数学核心素养的基本框架（如图1）。[8]

图1

第二种则是从国际视野的角度进行诠释，如蔡金法教授综观国内外人才培养目标，从数学学科角度归纳了4个数学核心素养的成分，分别是数学交流、数学建模、数学智能计算思维与数学情感。[9]其中数学情感引起笔者的重视，数学情感关注的是数学学习过程中形成的积极的非智力因素。这给我们以启示，“情感、态度与价值观”是数学课程目标之一，也应该是数学核心素养的成分之一。

（二）小学数学核心素养的建构

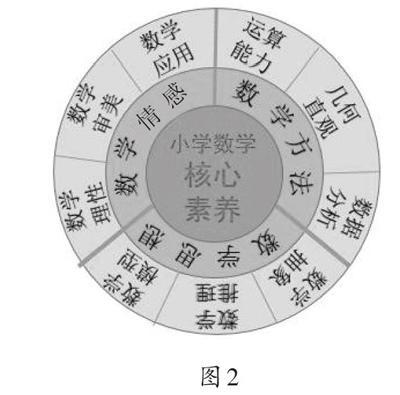
综合国内外专家就小学数学核心素养的论述，笔者把小学数学核心素养分成三个方面，分别是数学思想、数学方法与数学情感（如图2）。

图2

数学思想是指人在数学学习过程中形成的最一般的思维形式，包括数学抽象、数学推理与数学模型。它们与高中数学核心素养相对应，但表现形式更加浅显。数学方法是指在解决实际问题时结合问题特征形成的思维方法。如为了使抽象的数学问题更加形象直观而采用的几何直观;运算解决问题必须具备的运算能力;进行数据统计与分析随机事件而形成的数据分析能力。数学情感是指通过数学学习可以让学生形成积极的情感、态度与价值观，主要包括数学理性、数学审美与数学应用。通过现象发现本质的理性思维是数学思维的重要特征。数学的简洁性、抽象性、和谐性均展现着数学之美，通过数学学习让学生拥有数学美的体验。把数学应用归纳到数学情感，是指通过数学应用的广泛性让学生体会到数学学习的现实价值。

以上小学数学核心素养的构建，体现了传承、融合与完善，相信随着小学数学课堂教学改革的深入，会更加科学、更加合理。

三、从数学史中汲取数学核心素养的因子

论述数学史与小学数学核心素养的内涵，可以更好地把数学史融入数学教学，从数学史中汲取数学核心素养的因子。

（一）从数学史中汲取数学思想形成的线索

数学史中记录的数学知识产生与形成的过程，往往就是数学思想逐步萌芽与形成的过程。教师可以依据学生已有的认识基础和可接受性，让学生重走数学探究之路，体会数学思想的形成过程。

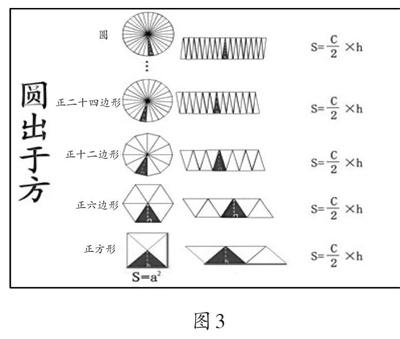
如圆的面积计算公式一般按极限思想完成推导。除此之外，也可以参考《周髀算经》中的“圆出于方”，把圆类比成正多边形，从推导偶数边正多边形通用面积计算公式后，用类比思想推导出圆的面积计算公式——“半周乘半径”（如图3）。[10]

图3

相对于数学教材，数学史更能够追溯到数学的本源，发现数学在产生和形成过程中体现出的数学思想，丰富学生对数学本源的认识。

（二）从数学史中汲取数学方法总结的素材

如曹培英老师归纳的，每一种数学方法往往与数学学习领域有联系。通过数学史，可以更好地回溯数学方法逐步总结的历程，选择合适的数学史料，进行教育学化加工，成为学习的素材。

如平均数，起源于估算一棵果树上的果实数，取其中一个枝丫上的果实数为代表，去乘这棵树的枝丫数。教师可以用这个数学史故事导入平均数的学习，通过分析、比较、完善引出平均数，以此培养学生的数据分析能力。又如数对的教學，可以用笛卡尔发明直角坐标的素材进行教学设计，让学生体会几何直观的魅力。

需要特别注意的是，从数学史中选择相应的数学素材，一定要结合学生的年龄特征，进行二次加工，使得情节更加生动直观，更加符合学生的认知规律，更加有利于学生体会数学的内在魅力。

（三）从数学史中汲取数学情感的积极体验

就小学数学而言，在数学史中体现数学情感积极体验的例子比比皆是，如通过讲述古代世界各地各种数码的历史与发展，可以感受到数学的简洁美与统一美;介绍圆周率的探索历史，可以培养数学的理性精神;通过列举自然界中的圆（如荷叶、向日葵等），生活中的圆（如车轮、土楼等），有寓意的圆（如月饼、太极图等），发现数学与生活之间广泛的联系。

学生积极的数学情感体验，应该来自于日常数学教学的渗透，教师可以从数学史中汲取生动的、有教育意义的数学史料，结合具体的数学教学内容情境再现，再通过设问，让学生谈体会、说感受。

“从数学家的废纸篓里寻找知识的源泉”，数学知识不会离开数学史而凭空产生，从数学史中汲取小学数学核心素养的因子，是探究与落实小学数学核心素养的重要途径。

参考文献：

[1]汪晓勤. HPM：数学史与数学教育[M]. 北京：科学出版社，2017.

[2]宋乃庆.小学数学文化读本（丛书）[M]. 重庆：西南师范大学出版社，2016.

[3]邵汉民.小学数学史料与数学教学[M]. 北京：科学出版社，2014.

[4]蔡宏圣. 捕捉数学史中的教育基因[J]. 人民教育，2008（6）：38-40.

[5]邵汉民. 小学数学教学探究（上）[M]. 杭州：浙江工商大学出版社，2013.

[6]邵汉民，沈国灯. 从数学史料中寻找数学教育的因子[J]. 教学月刊·小学版（数学），2016（10）：25-27.

[7]中华人民共和国教育部.普通高中数学课程标准（2017年版）[M]. 北京：北京师范大学出版社，2019.

[8]曹培英. 小学数学学科核心素养及其培育的基本路径[J]. 课程·教材·教法，2017，37（2）：74-79.

[9]蔡金法，徐斌艳. 也论数学核心素养及其构建[J]. 全球教育展望，2016，45（11）：3-12.