基于双eN方法的短舱层流转捩影响因素
2019-12-09孟晓轩白俊强张美红王美黎何小龙汪辉
孟晓轩,白俊强,张美红,王美黎,何小龙,汪辉
1.西北工业大学 航空学院,西安 710072 2.西北工业大学 无人系统技术研究院,西安 710072 3.中国商用飞机有限责任公司 上海飞机设计研究院,上海 201210
现代民用飞机,尤其是民航客机,越来越追求经济性和环保性[1],为提高大型民机的空气动力学效率,大幅降低民机的油耗和污染排放,层流控制技术是一种极具减阻潜力和应用前景的方法[2-4]。大涵道比涡扇发动机技术的快速发展带来了发动机几何尺寸的迅速增加,发动机阻力占全机阻力的比重也迅速增加,而短舱表面的摩擦阻力是短舱阻力的重要来源之一,因此对短舱外表面进行自然层流设计,能有效减小摩擦阻力,提升全机的经济性。此外发动机短舱对升力、力矩等气动性能要求较低,约束较少;且不受附着线转捩问题的影响,因此短舱的层流减阻设计具有较高的可行性[3]。经自然层流(Natural Laminar Flow, NLF)设计的短舱称之为自然层流短舱。
国外学者针对NLF短舱已开展过许多研究工作。美国兰利研究中心[5]从20世纪80年代中期开始对发动机短舱的层流控制技术进行了可行性研究,经分析认为层流控制技术有可能使短舱摩擦阻力减少约5%。Younghans和Lahti[6]在1984年利用实验手段对单独短舱和翼吊短舱进行了层流设计,在其外表面上均实现了大面积层流。德国宇航院(DLR)、罗尔斯-罗伊斯和MTU(Motorenund Turbinen-Union Friedrichshafen)[7]合作进行了自然层流短舱的飞行试验,短舱表面的层流区达到了60%,且研究还表明噪声和振动对层流控制的影响很小。Lin等[8]利用γ-Reθt转捩模型预测了NLF短舱表面的转捩现象,同试验结果相比该方法还需进一步完善。目前,中国对自然层流的研究多集中在机翼上[9],针对NLF短舱的相关研究较少,何小龙等[10]基于EFFD(Extended Free Form Deformation)参数化方法进行了NLF短舱和带动力NLF短舱的优化设计,取得了较好的结果。
发展高效可靠的转捩预测方法有助于研究短舱的流动特点并进行层流减阻设计。常见的工程转捩预测方法有基于湍流模式理论的γ-Reθt转捩预测模式和基于线性稳定性分析的eN转捩预测方法。γ-Reθt转捩预测模式是由Menter和Langtry[11-12]等提出的经验预测模型。经典的γ-Reθt模型仅能考虑到沿流向的间歇因子变化规律,对流向T-S波不稳定性引起的转捩进行预测。为能对CF波引发的不稳定性转捩进行准确预测,Owen和Randall[13]于1952年率先提出Recf横流转捩判据,应用起来比较复杂。Arnal等[14]在1984年提出了C1准则判据,应用比较广泛。之后德国宇航院的Grabe等[15-16]通过当地化求解横流雷诺数,耦合C1准则进行横流转捩研究。中国学者[17-19]也先后展开了对横流转捩预测方法的研究。
中国对流动稳定性的研究以天津大学周恒院士团队为代表[20],做了大量的基于稳定性和直接数值模拟(DNS)的研究。Lee和Wu[21-22]在平板转捩实验中揭示了非线性边界层不稳定性和湍流发生的一种特征流动结构,提出了一种由类孤立波主导的转捩物理过程。李新亮等[23]做了大量的基于DNS的转捩过程研究,然而其主要研究焦点是高超声速下的转捩过程机理,即面向航天工程需求。面向航空问题,基于求解线性稳定性方程而发展的完全eN方法,由Smith[24]和Ingen[25]等首次提出,是目前航空界最被接受和广泛认可的方法。eN方法的思想是对边界层流动中的小扰动进行线性稳定性分析,如果扰动逐渐衰减,则是稳定的,如果扰动被放大,则是不稳定的。对于不稳定的扰动,从其开始放大处起,沿下游方向计算其累积线性放大倍数,当累积放大倍数到达扰动开始放大处振幅的eN倍时,认为转捩发生。在转捩点上所对应不稳定波的幅值放大因子的包络线值为转捩关键N因子(Ncrit)。eN方法对N的积分策略有很多种,如固定β法、包络线法、双eN方法等。双eN转捩预测方法针对T-S波和CF波选择不同的扰动放大率积分策略,可以同时计算T-S波和横流不稳定性扰动诱导转捩。在飞行试验数据分析中发现,NTS-NCF双因子策略的一大好处是,在沿无黏流线附近方向T-S波的激发过程很相近,幅值增长率都很相似,因此在马赫数不大于1的情况下,沿着边界层无黏流线方向对N因子的计算可以反应T-S波增长的过程。而对低湍流背景的后掠机翼上的横流转捩,横流驻波的初始振幅比横流行波的振幅要大得多,因此双eN策略对航空外流的分析误差不大。朱震等[26]利用双eN方法开展了翼身组合体复杂三维外形的转捩预测研究,得到了较好的预测结果。另外,应用双eN策略计算飞行试验结果时所取得的关键值(NTS,NCF)的分布都求解的是不可压稳定性方程。为和已有的工程经验对比,本文也只求解不可压稳定性方程。
工程上除直接求解线性稳定性方程的eN方法外,还发展出来有eN-数据库[27-28]方法。eN-数据库方法在计算时不再求解稳定性方程,而是直接根据边界层形状因子、速度型等信息在数据库中查找平板边界层流动的不稳定扰动累积放大因子的包络线,从而确定N值。eN-数据库方法由于不需要求解稳定性方程,具有计算速度快的特点,但只适用于机翼这类构型的绕流流动,对于非机翼类构型,如椭球、短舱以及机身等构型,eN-数据库方法并不适用。基于非线性稳定性分析的方法,如将抛物化稳定性方程(PSE)和CFD耦合求解的方法[29],近年来已有工程化的程序出现,能够比较方便地考虑边界层内非平行流和非线性的影响,较好地描述边界层内的流动结构和扰动形态,但其控制方程为抛物型偏微分方程,不是当地特征值问题,需要给定入口边界条件沿流动方向向下游推进求解,使用不便,且存在稳定性方程求解计算量大的缺点。
现已发展的诸多工程转捩预测方法,无论是经典的γ-Reθt转捩预测模式或者考虑横流不稳定性转捩而改进的γ-Reθt转捩预测模式,还是eN-数据库方法或者基于求解线性稳定性方程的eN方法,多集中在对翼型、机翼或翼身组合体等构型的转捩预测上[30-31],侧重于机翼绕流的转捩预测研究。针对短舱这类具有显著三维效应的类圆柱形构型,在求解过程中,由于短舱不能同机翼一样通过求解边界层方程的方法获得层流速度型,只能直接从CFD流场中提取边界层速度型进行稳定性分析,因此计算量较大。国内外也鲜有相关文献研究层流转捩预测方法在短舱上的应用,在这类构型上有关层流转捩的试验数据储备也不是很多。
由于NLF短舱在大型民机减阻设计上具有较高的可行性和可观的发展前景,针对短舱表面的层流优化设计就日趋重要,开展短舱层流转捩的影响因素研究对NLF短舱的优化设计具有较强的指导意义。本文基于线性稳定性分析理论,从CFD流场中直接提取边界层速度型信息进行稳定性分析,将NTS-NCF双因子转捩判断模块同高精度雷诺平均Navier-Stokes(RANS)求解器[32]耦合,建立了一套可同时计算T-S波和横流不稳定性扰动诱导转捩的流动转捩自动判断方法,对影响短舱层流转捩的因素进行研究。
1 双eN转捩预测方法
本文所用双eN转捩预测方法的具体求解过程如图1所示。首先设定初始转捩位置,使其尽量靠近模型后缘从而得到足够大的层流区域,利用RANS求解器计算流场,使用SA湍流模型模拟湍流流动。在CFD计算结果中提取边界层信息,如速度、速度梯度、温度、温度梯度等,传递进入线性稳定性分析求解器,分别计算幅值放大因子NTS和NCF的包络线,并利用转捩判据判断转捩位置,将计算得到的转捩位置反馈到CFD求解器中,进行再一次的循环计算,直到循环得到的转捩位置不变为止。
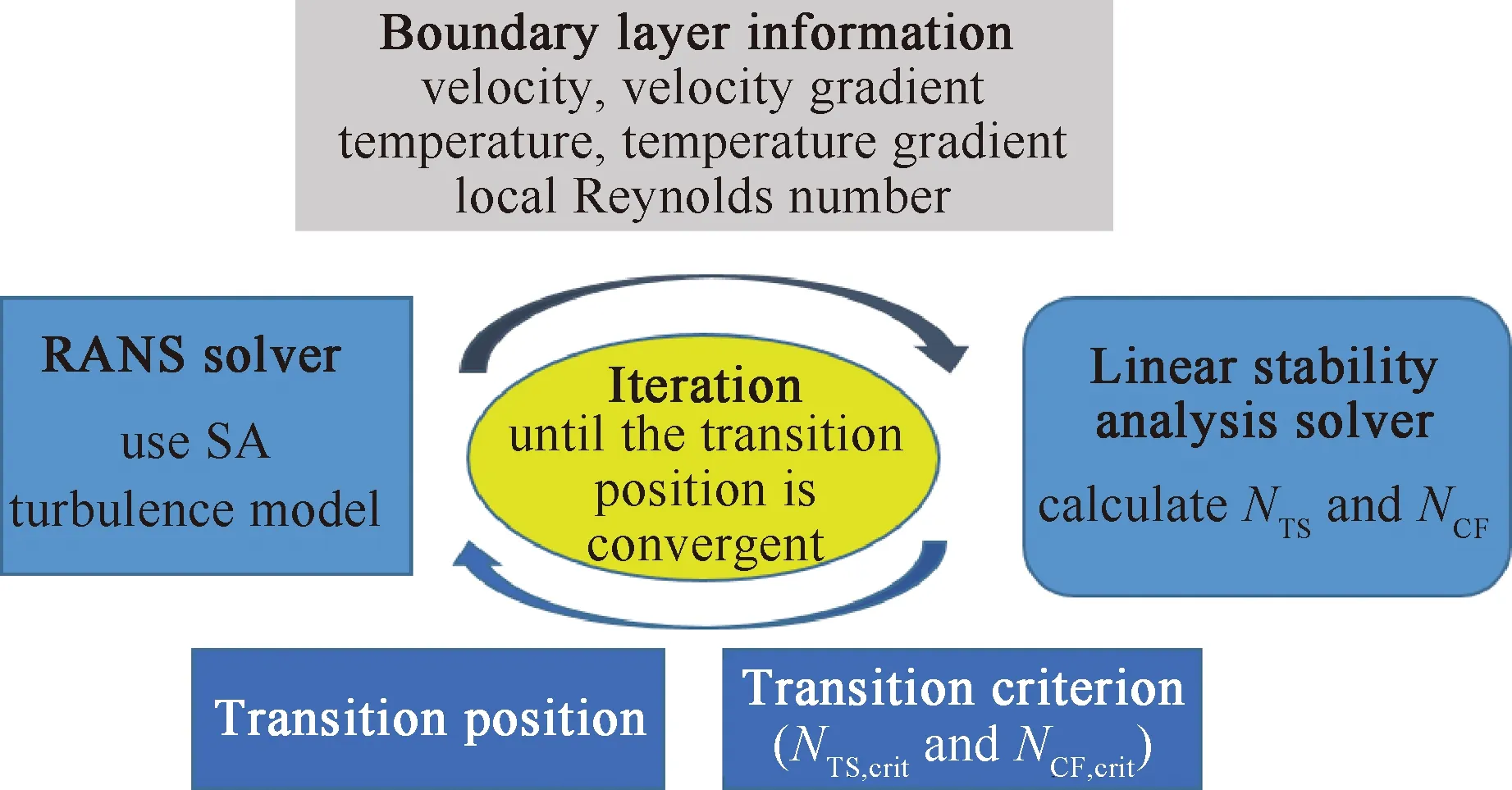
图1 RANS求解器耦合eN稳定性分析方法求解流程Fig.1 Solution for RANS solver coupling eN stability analysis method
1.1 边界层信息提取
在边界层内分布超过80个网格点,模型前缘附近物面周向均布32个点。设定初始转捩位置,将位于转捩位置上游的模型表面和距表面0.01 m厚的区域都定义为层流,关掉湍流模型的产生项,进行CFD计算可得到层流区。沿着32个点依次向上游和下游寻找无黏流线:向上游寻找,直到驻点;向下游寻找,直到设定的转捩位置或者流动分离点。将无黏流线投影到物面上,每隔一段距离记录一个坐标,作为稳定性分析的坐标点存储在程序中。
沿指定点的法向方向,在每个点上提取边界层信息,利用可压缩伯努利方程计算边界层顶部的速度Ue,取95%Ue处的壁面法向位置为边界层顶部,记录当地的速度矢量,将该点位置信息和法向方向与壁面交汇的点对应。该方法对于压力梯度不大或者负压梯度区域的流动,近似效果较好。而对靠近前缘这些顺压梯度很大的位置,需要进行适当的修正:该区域的边界层内是有黏有旋流动,涡量和平均应变率都很大,比值接近1,而在边界层外是无黏无旋流动,涡量很小,平均应变率较大,因此可以利用涡量和平均应变率的比值是否为1来修正边界层外缘的位置。
沿无黏流线记录的坐标沿法线向物面投影,确定分离点、压力最小值点:分离点用物面摩擦系数确定,表面极限流线方向和无黏流线方向的内积为负的第1个点即为分离点;而压力最小值点为沿无黏流线方向的压力最小值点。将分离点、压力最小值点依照计算的是T-S波主导的转捩还是CF波主导的转捩,作为计算相应N值时积分的终止位置。具体计算时,若仅对CF波转捩进行分析,可仅对幅值增长率积分至压力最小值点。
在CFD流场中,根据无黏流线上记录的坐标点和沿法向投影到壁面上的点,在两点确定的区间上对流场信息进行插值,提取边界层信息,包括速度、温度、密度、压强等。将速度矢量沿无黏流线方向投影得到流线方向的流向速度U和横向方向的横流速度W,进而得到速度梯度的二阶空间导数,利用当地的温度、密度等信息,可以计算当地雷诺数。这些信息将会在求解线性稳定性方程中使用。
1.2 线性稳定性分析
稳定性方程的分析方法有时间模式(Temporal Theory)和空间模式(Spatial Theory)两种,分别从不同角度分析问题,利用群速度的关系可以导出相互变换关系。本文选择用时间模式分析稳定性方程,具有编程简单、易于实现的优点。
对于给定的扰动,指定其扰动频率,随着边界层增厚,扰动幅度在中性点x0的下游开始增加,之后在下游某一位置xl下降,如图2所示,图中x为沿扰动波传播方向的坐标,f为扰动波频率,A为扰动波的幅值,N为扰动波的幅值放大因子。因此,从x0到xl处沿扰动波传播方向的积分即为中性点总的幅值增长率,定义为
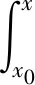
(1)
式中:αi为空间扰动波的幅值放大率。对于一系列含有不同频率的扰动,可以得到总的幅值增长率的曲线系,其包络线定义为
N=max[ln(A/A0)]f
(2)
式中:N为幅值放大因子,是一个比值,包含的是最容易被放大的扰动波的集合。
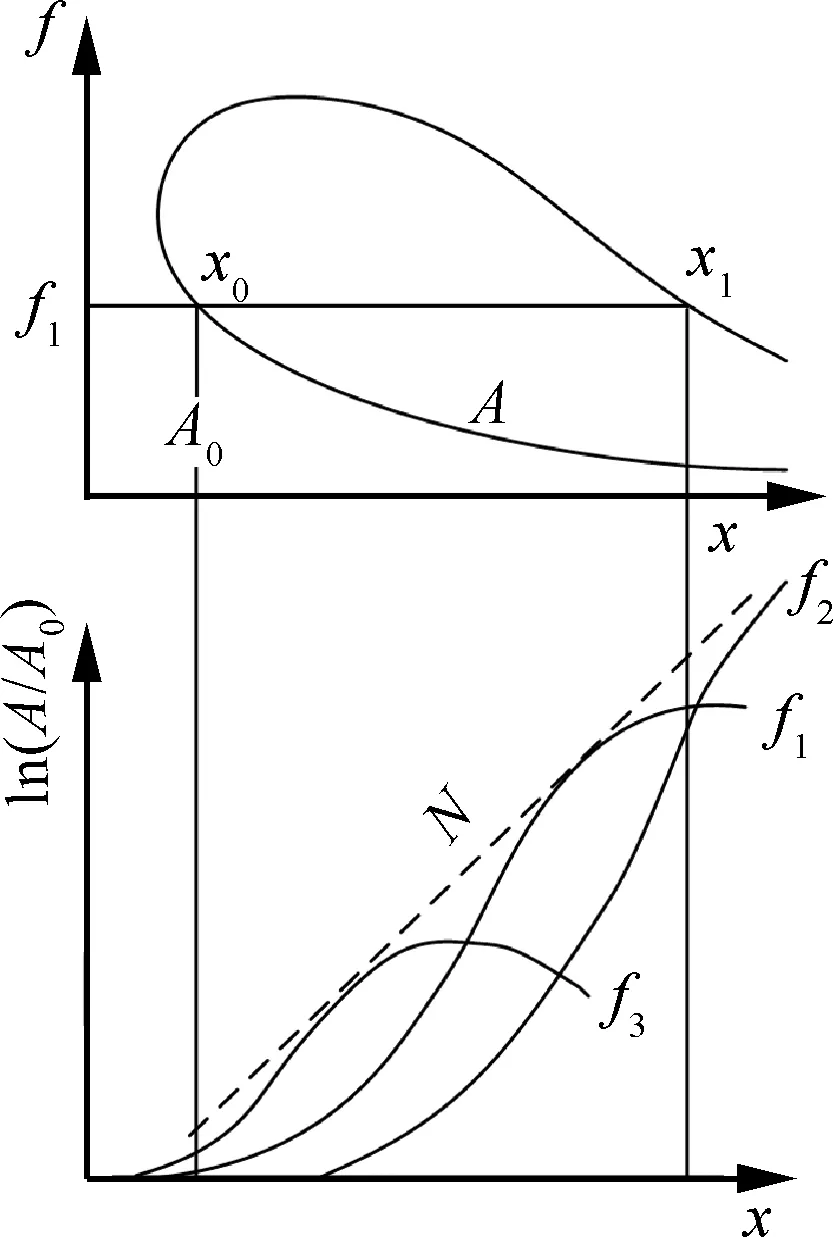
图2 中性曲线(上)、幅值增长曲线与包络线(下)Fig.2 Neutral curve (up), amplitude growth curves, and envelope lines (low)
首先,沿着每一条无黏流线方向,初步计算沿该方向的一条中性曲线,得到扰动的稳定区域和不稳定区域的分界线。通过中性曲线确定不稳定扰动的频率范围、波数范围和不同扰动各自开始被放大的位置,从而确定沿无黏流线方向所需考虑的点,即仅从中性曲线所包含的不稳定区范围内对幅值放大率进行积分。在每个站位进行稳定性分析时,对确定的波数范围分成40个流向波数α′和横向波数β′的组合,对每个点求解线性稳定性方程,对这些频率的扰动放大率从中性曲线下半支出发,沿着扰动传播路径(近似在势流方向)进行积分,积分至下游的分离点或者压力最小值点或者指定点,得到扰动累积放大因子N。
短舱上常见的转捩样式是自然转捩,包括自由来流中的扰动穿过边界层在边界层里触发的T-S波引起的T-S转捩和因为横流速度存在引起的横流转捩。在亚声速时,T-S波的传播方向和x方向夹角几乎为0°,而横流驻波的传播方向和x方向夹角为85°~90°。因此本文采用固定波角法分别计算NTS和NCF,对于NTS,固定波角ψ=0°,即边界层外边界速度方向;对于NCF,采用同时固定其频率和波角的方法计算CF波扰动累积放大因子,固定其频率f=0 Hz,固定波角ψ=90°。
1.3 转捩判断
1.3.1 T-S转捩判据
众多试验表明来流湍流度对转捩有很大的影响,根据Dryden湍流度为0.1%、1%的试验数据,Mark[33]总结出放大因子与湍流度相关联的表达式,即Mark关系式:
N=-8.43-2.4ln(Tu)
(3)
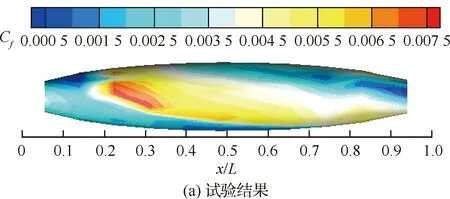
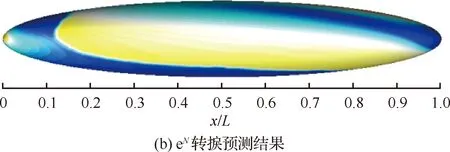
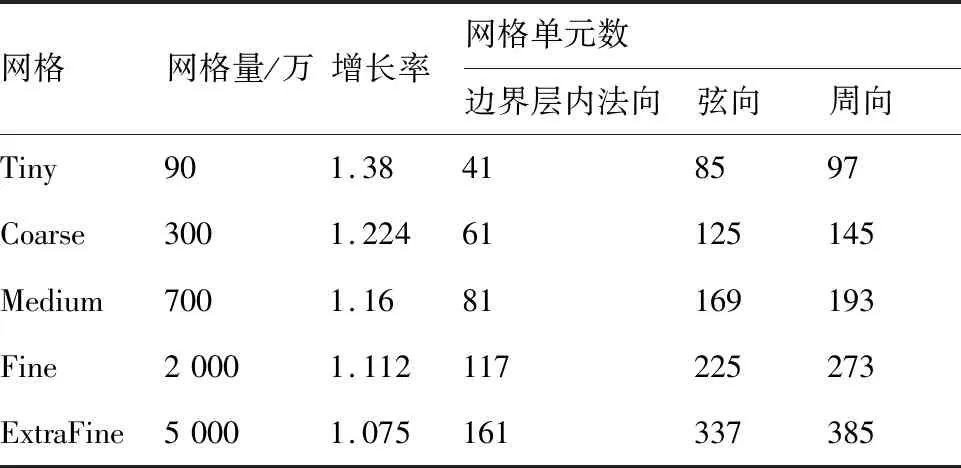
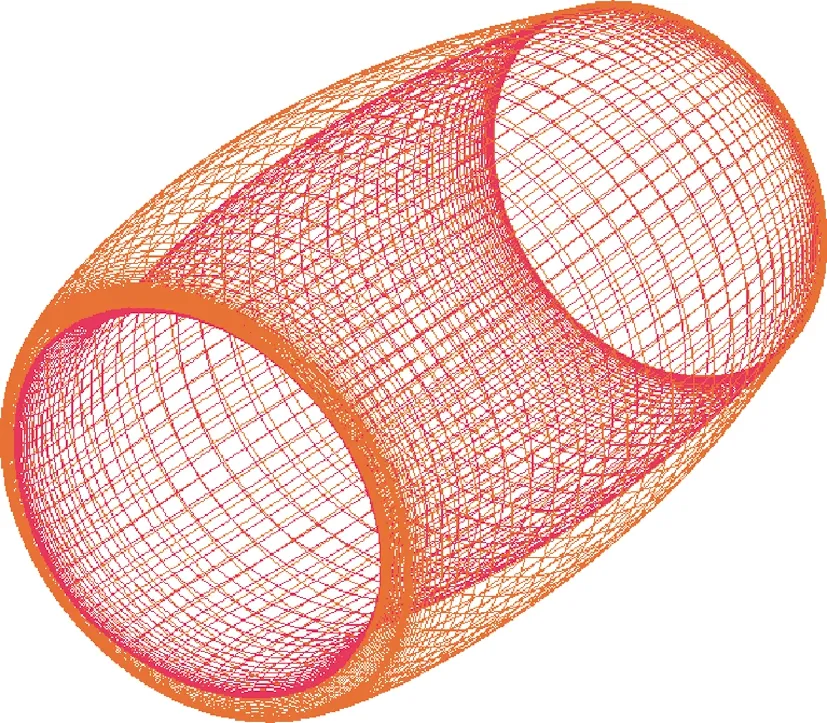
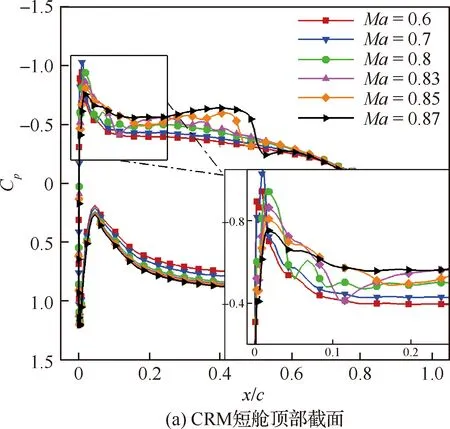
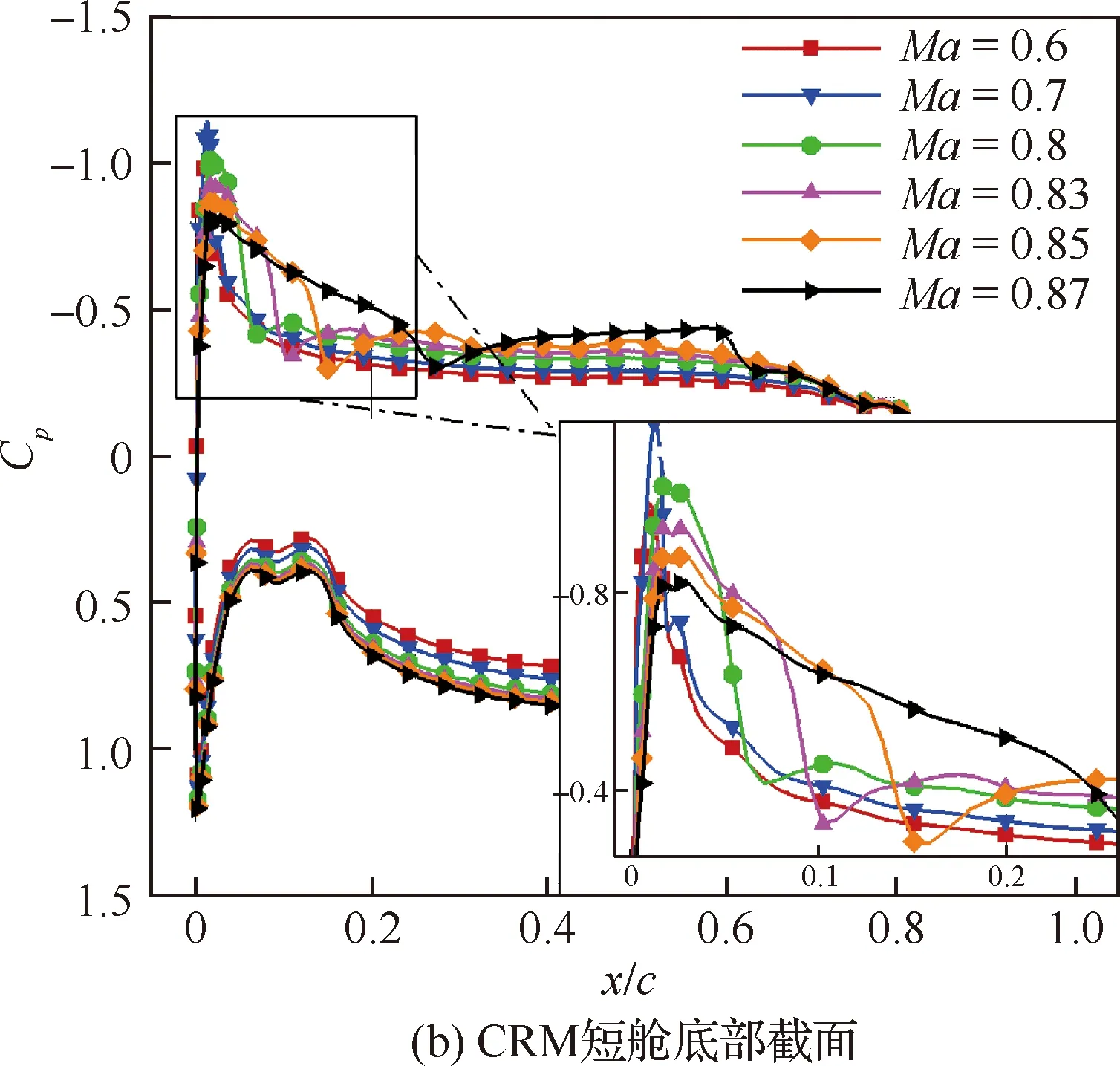
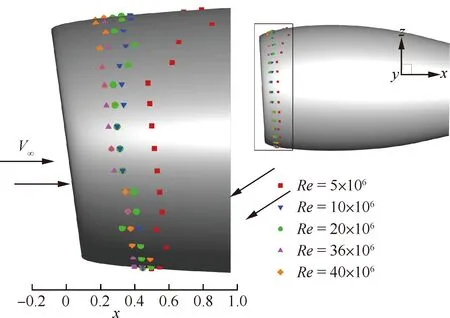
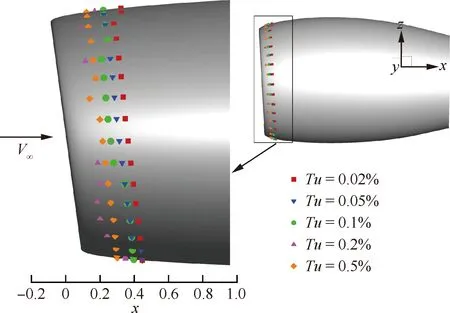
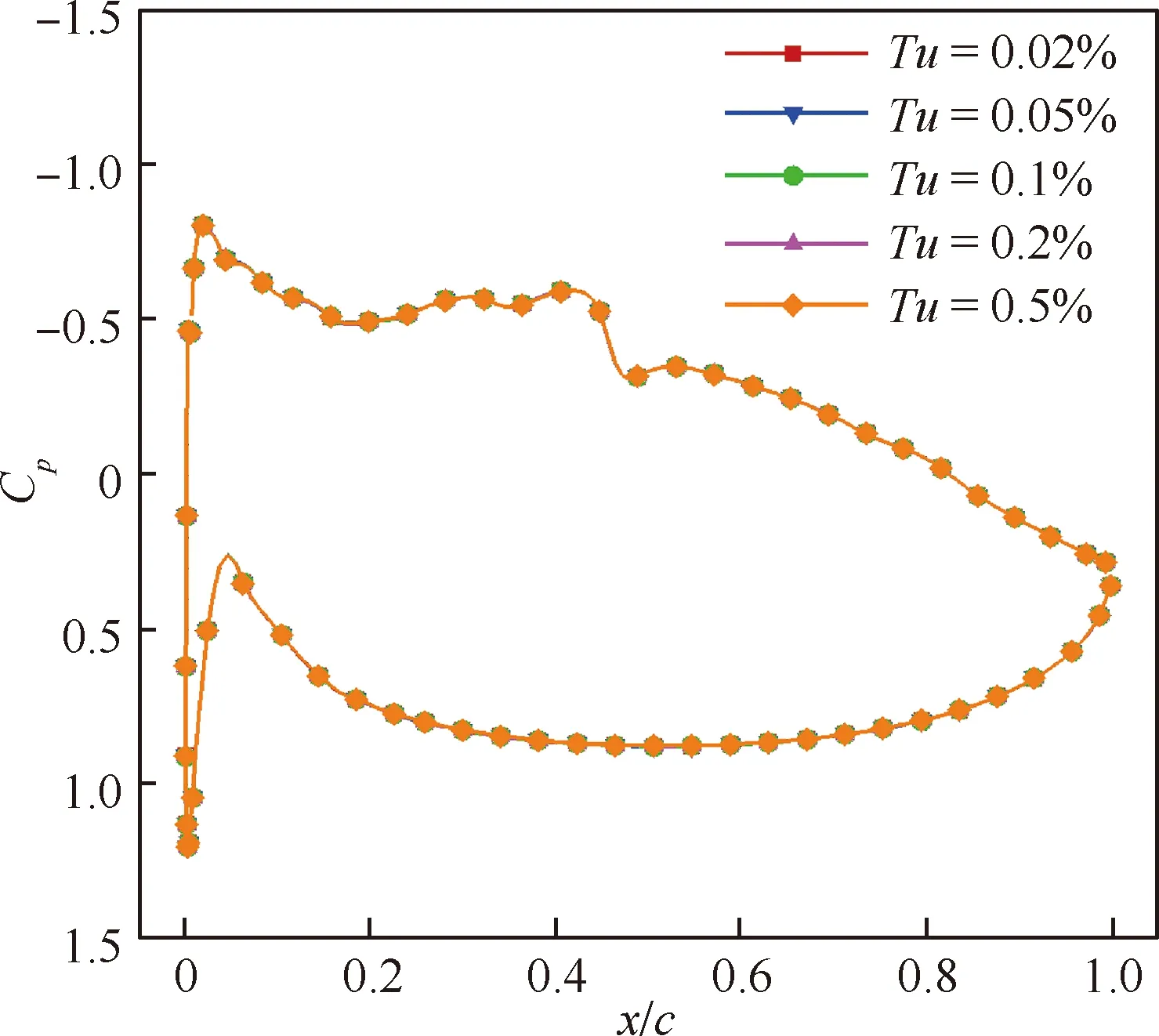
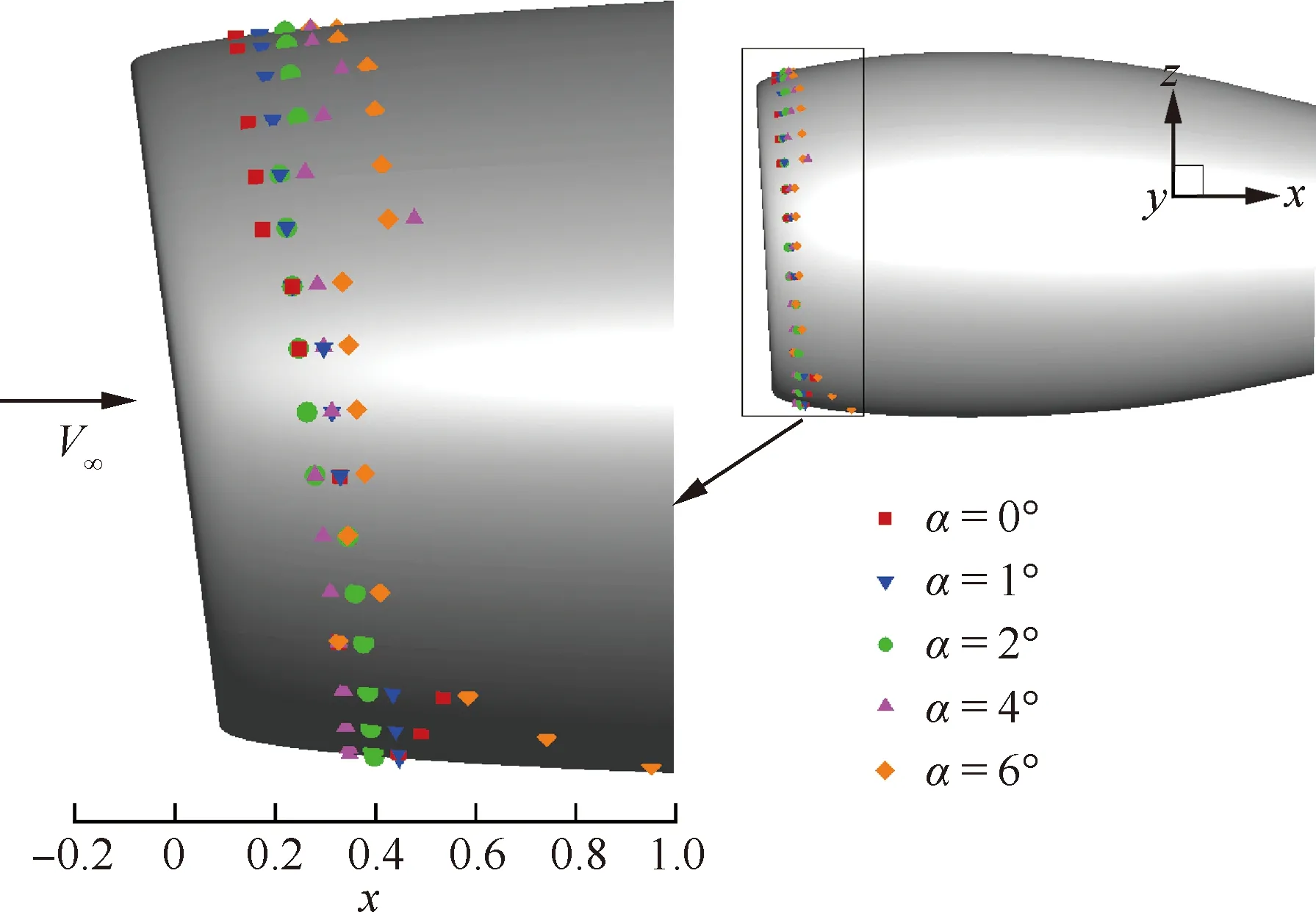
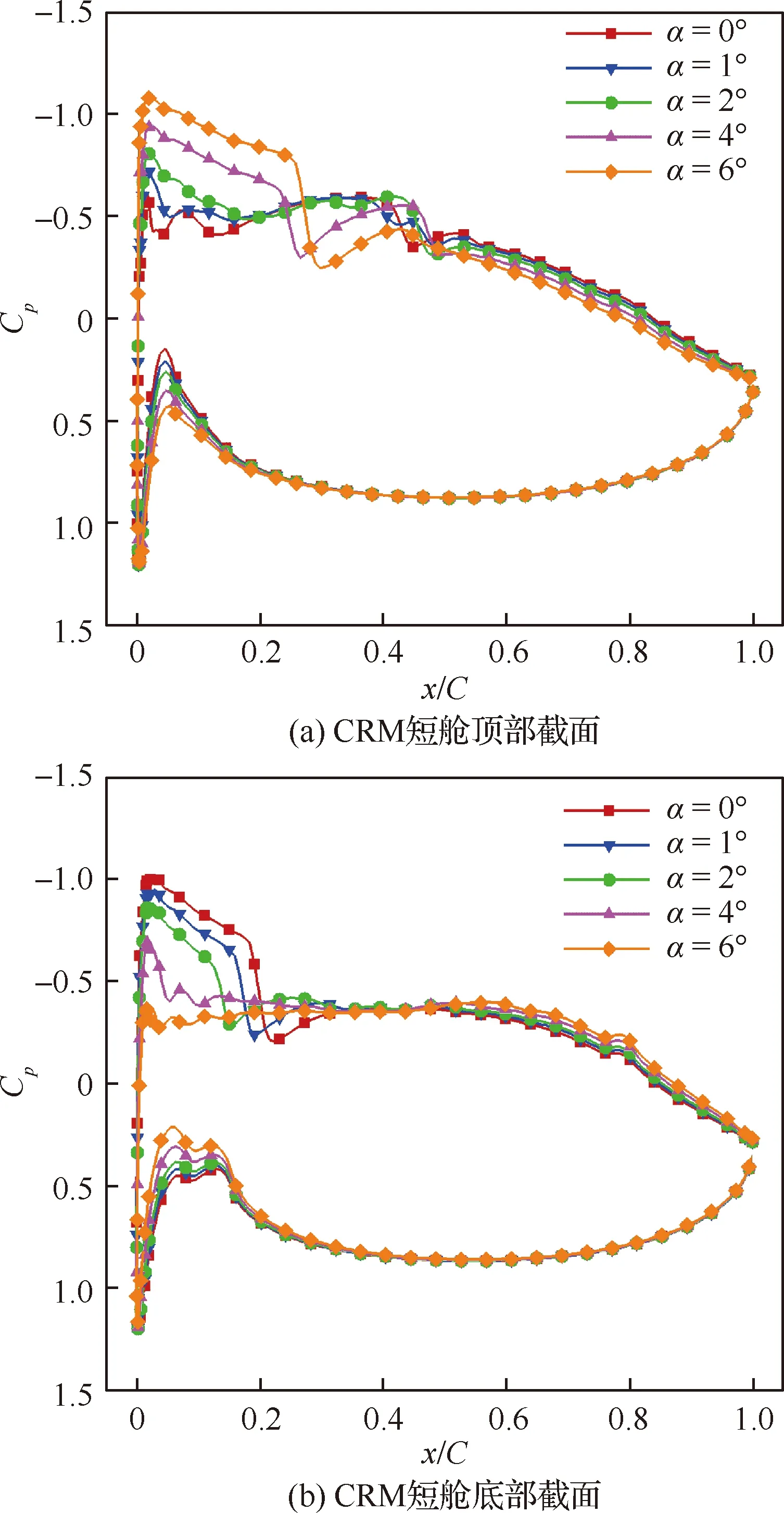
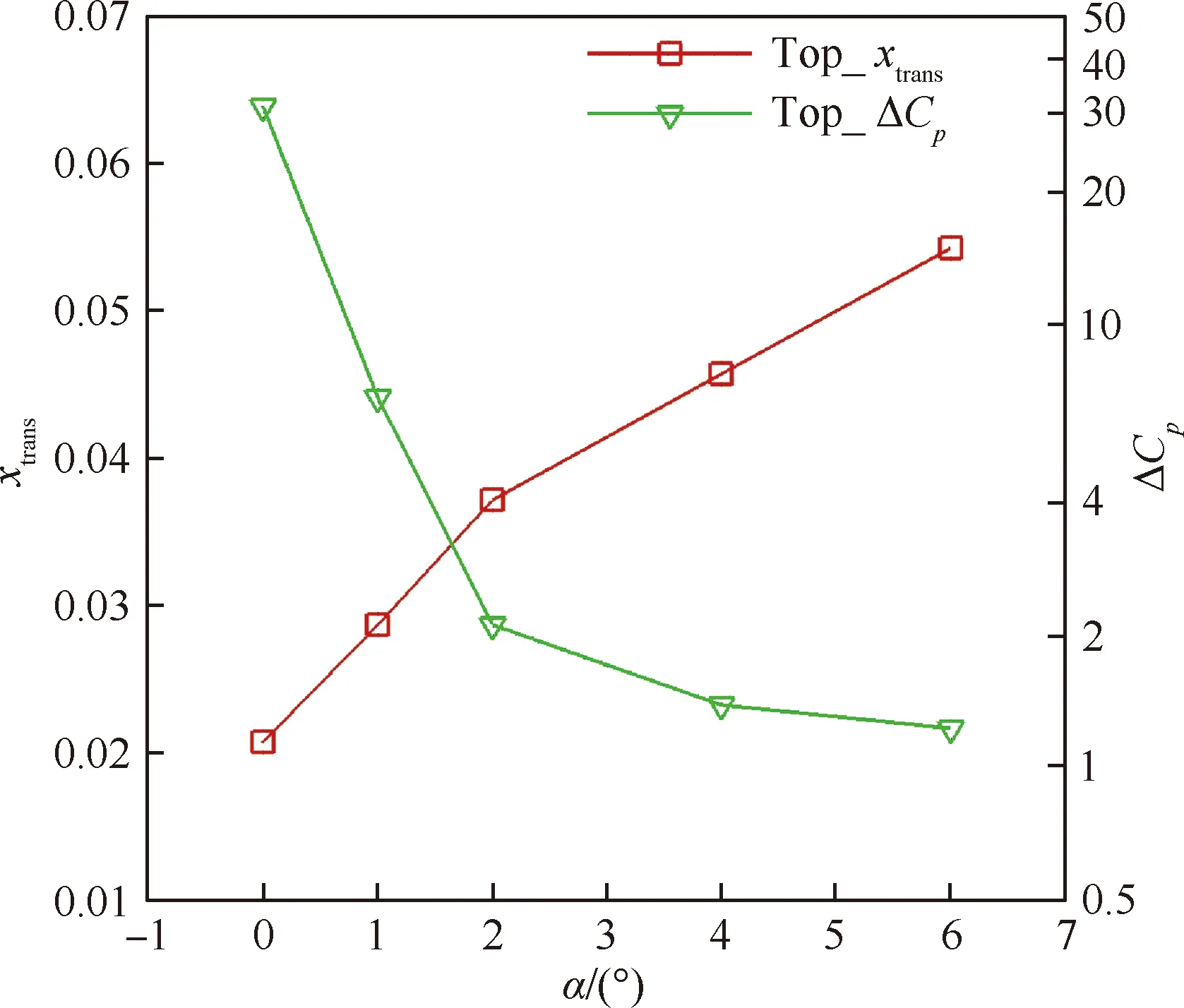
如果0.1% 图3为Mark关系式给出的转捩雷诺数RexT与湍流度相关曲线,图中,湍流度Tu采用对数坐标。可以发现,式(3)在特别低的湍流度下,不具有参考价值。而一般实际飞行条件下的湍流度都小于0.05%,此时,NTS.crit的值依赖于飞行试验确定。 图3 Mark关系式和不可压平板转捩预测试验对比Fig.3 Comparison of Mark formula and incompressible plate transition prediction test 1.3.2 CF转捩判据 对于CF波转捩阈值NCF.crit,其关键值依赖于模型表面的加工状况,即表面粗糙度和具体的飞行条件。在缺少相关试验的条件下,参照风洞中NLF0415机翼横流转捩的标定研究,采用NCF.crit=6.4[35]这一固定值进行计算。 当不稳定扰动在下游某点处累积的线性放大倍数达到扰动开始放大处振幅的eN,crit倍时,认为转捩发生,该点即为对应无黏流线的转捩位置。将转捩位置反馈给RANS求解器开始新一轮的循环,反复迭代直到转捩位置收敛时终止,输出转捩位置。 为验证双eN转捩预测方法的可靠性和适应性,下面针对6∶1标准椭球体(椭球体长矩L=2.4 m,短矩D=0.6 m)模型进行转捩预测。该模型由德国宇航院进行了多个迎角和雷诺数的风洞试验,试验数据比较详实和全面。CFD计算网格为800万,附面层第1层网格为1.2×10-6m,法向增长率为1.1,物面网格的y+均小于1。迎风端对称面的角度Φ=0°,背风端对称面的角度Φ=180°。自由来流湍流度为0.1%,黏性比为10。根据经验关系式设定eN方法中的N值为:NTS=8,NCF=5.5。利用该方法对椭球的典型转捩现象进行了数值模拟。图4为标准椭球在Ma=0.136、α=15°、Tu=0.1%、Re=6.5×106状态下试验与eN方法计算所得摩阻系数Cf分布云图的对比结果。 图4 试验和eN转捩预测方法所得椭球转捩位置对比Fig.4 Comparison of ellipsoid transition position obtained by test and eN transition prediction method 从计算结果可以看出,本文建立的双eN稳定性分析转捩预测方法能够较好地预测出椭球体边界层内出现的横流不稳定性转捩现象,具有较高的预测精度,由此验证了双eN线性稳定性分析转捩预测方法对于类圆柱构型表面的层流转捩现象具有较强的模拟和预测能力。 为了对短舱层流转捩的影响因素进行研究,本文选择CRM模型的单独短舱为研究对象,并对该短舱构型进行网格收敛性验证。本文选择的CRM模型由NASA的亚声速固定翼空气动力技术研究小组和DPW的组织委员会合作设计开发,为CFD的验证和确认工作提供基准外形[36]。 从CRM翼身组合体中分离出单独短舱,通过平移旋转变换使短舱轴线与x轴重合,以轴线前缘点为坐标原点。以CRM翼身组合体的参考面积、展长为短舱的参考面积、展长,以短舱的轴向长度为短舱参考弦长。短舱的参考面积S=191.85 m2,参考展长B=29.38 m,参考弦长c=5.966 m,以平均气动弦1/4弦线位置(1.492 m, 0 m, 0 m)为短舱力矩参考点。 参考CRM翼身组合体设计工况,选择短舱基准工况如下:高度H=11.277 6 km,自由来流马赫数Ma=0.85,迎角α=2°,侧滑角β=0°,基于短舱参考弦长的雷诺数Re=36.779×106,来流初始湍流度Tu=0.1%,黏性比Rt=10。强迫湍流度在上游远场保持不变,在短舱前缘开始自由衰减。采用SA湍流模型模拟湍流流动,转捩阈值根据经验取NTS.crit=8.1,NCF.crit=6.4。 选择90万、300万、700万、2 000万和5 000万5个不同密度的网格,计算短舱基准工况,进行网格收敛性验证,各网格的基本信息如表1所示。所有网格壁面第1层网格高度均为1×10-6,满足y+<1的条件。图5给出了网格量为700万的短舱表面网格。图6为不同密度网格对短舱阻力系数CD的影响,图7为不同密度网格计算的短舱顶部截面压力系数Cp分布曲线。 从图7所示不同密度网格下计算的压力分布曲线来看,基准状态下短舱外表面的主要流动特点是:前缘附近很快达到吸力峰值,下游完全处于逆压梯度区,中间某处存在一个激波,在上表面激波位于45%短舱长度,在下表面激波位于15%短舱长度,左右两侧激波较弱,位于20%短舱长度。90万网格(Tiny)没有很好地模拟压力系数沿流向的变化趋势,也没能准确捕捉到短舱上表面存在的激波。结合图6中网格量对计算精度的影响,权衡计算精度和计算效率后,选择700万网格量(Medium)对短舱层流转捩的影响因素进行分析。 表1 不同密度网格的基本信息Table 1 Basic information for different density meshes 图5 短舱表面网格Fig.5 Surface mesh of nacelle 图6 不同密度网格对短舱阻力系数的影响Fig.6 Effect of different density meshes on nacelle drag coefficient 图7 不同密度网格所得短舱顶部截面压力系数分布曲线Fig.7 Pressure coefficient distribution curves of nacelle top section obtained from different density meshes 所研究的马赫数变化范围为0.6~0.87,覆盖高亚声速到亚声速的工况。在马赫数0.8~0.87之间研究了4个状态点,详细分析了巡航马赫数附近短舱外表面转捩位置对飞行速度的敏感性。 随马赫数变化的最显著特征为:马赫数升高,转捩位置xtrans向下游移动,如图8所示,图中,V∞为来流速度。从压力分布随马赫数变化的关系中可以看出,马赫数增加引起短舱2个典型站位的压力分布发生很大变化,且具有相同的发展趋势,即随着马赫数增加,气流压缩性越来越强,负压峰值难以维持很高的值,负压峰值下降,下游的压力梯度随之减小,如图9所示,激波被推迟但激波强度增强,图中:压力系数采用对数坐标。在图10所示的压力分布局部放大图中,可以通过压力分布随位置变化的陡峭程度看出前缘附近压力梯度的变化规律。由于T-S波对压力梯度变化敏感,在飞行雷诺数下,越强的逆压梯度引起T-S转捩越早发生,因此得到转捩位置随马赫数升高而向下游变化的规律。 图8 CRM短舱转捩位置随马赫数变化Fig.8 Variation of CRM nacelle transition position with Mach number 图9 短舱前缘压力梯度和转捩位置随马赫数变化Fig.9 Variation of pressure gradient and transition position of naceller leading edge with Mach number 图10 不同马赫数下CRM短舱各截面压力系数分布Fig.10 Pressure coefficient distribution of each crosssection of CRM nacelle with different Mach numbers 雷诺数覆盖了(5~40)×106的变化范围。由于国内目前没有可靠的运行高雷诺数条件下静声风洞的条件和经验,因此进行了中等雷诺数到高雷诺数的计算与分析,研究转捩位置对雷诺数的敏感性,对标风洞试验可能出现的所有工况。 随着雷诺数增加,转捩位置有明显向前移动的趋势,如图11所示。雷诺数增加到10×106以上,移动位置变得不明显。而图12的压力系数分布对比结果表明,在相同马赫数、迎角条件下,短舱上的压力系数分布随雷诺数变化很小。因此,在相同的压力梯度作用下,雷诺数增加,层流更难以保持,带来转捩位置向上游移动。 图11 CRM短舱转捩位置随雷诺数变化Fig.11 Variation of transition position of CRM nacelle with Reynolds number 考虑的自由来流湍流度变化范围为0.5%~0.02%,包括0.5%、0.2%、0.1%、0.05%和0.02%。在巡航飞行工况下,对应飞行高度上的来流湍流度很低,一般认为在0.05%以下。在起飞和着陆过程中,在不同的风况和飞机飞行速度下,来流湍流度变化范围为0.05%~0.1%。对常规跨声速风洞,一般湍流度在0.2%~0.5%,而对静声风洞,湍流度可以下降到0.05%以下。中国目前缺乏静声风洞,因此将湍流度敏感性分析扩展到试验和飞行中所能遇到的所有工况,覆盖大湍流度的飞行条件和背景噪声非常低的安静飞行条件。 湍流度表征自由来流中扰动的强度,扰动传递到边界层产生不稳定波,在低湍流度下,扰动线性增长,当扰动波幅值增长到一定程度时,非线性影响增强,发生二次失稳或三波共振,很快发生转捩,称为自然转捩。在高湍流度下,较强的初始扰动将跳过线性增长阶段直接发生旁路转捩(Bypass);在本文研究的0.02%~0.5%湍流度范围内,扰动较弱,其转捩途径一般为自然转捩,此时双eN方法能够反映扰动的线性增长过程,较好地进行转捩预测。 如图13所示,随着湍流度增加,扰动变强,转捩更容易发生,转捩位置向上游移动,从短舱长度的10%位置向前移动到5%位置,变化范围很小。流动的压力系数分布不随湍流度的变化而变化,如图14所示。 图13 CRM短舱转捩位置随湍流度变化Fig.13 Variation of transition position of CRM nacelle with degrees of turbulence 图14 不同湍流度下CRM短舱顶部截面压力系数分布Fig.14 Pressure coefficient distribution of top section of CRM nacelle with different degrees of turbulence eN转捩预测方法计算无黏流线方向N增长的包络线,在前缘附近是一条以沿流向位置为函数的斜率很大的直线,在不同湍流度时,利用Mark关系式建立转捩判据,因而能够分辨出不同湍流度的影响。由于在很高的雷诺数下,N增长的包络线是一条斜率很大的直线,在很大的湍流度变化范围内,转捩位置的变化范围在5%短舱长度以内,表明在高雷诺数工况下,该短舱上的转捩位置对湍流度的变化很不敏感。 对于迎角来说,若偏离设计点过大,流动带来的分离问题导致气动力变化引起问题的严重性远远大于转捩位置移动带来的阻力变化。因此,仅考虑0°~6°的小迎角范围。 随着迎角的变化,转捩位置在短舱的迎风面和背风面上出现较小变化,如图15所示。迎角的变化引起了压力分布的明显变化,如图16所示:在上表面,随着迎角的增加,吸力峰值增加,压力梯度缓慢减弱,激波增强。计算的转捩位置在上表面向下游有小幅的移动,移动的范围在5%短舱长度以内,如图17所示。主要原因是压力梯度的变化幅度不大,所以作用效果不显著。在下表面,随着迎角的增加,外表面的压力梯度增加,吸力峰值下降,和上表面变化趋势相反,转捩位置向前缘唇口移动,但是在6°迎角,逆压梯度增加,逆压梯度变化量的绝对值很小,不足以迅速激发T-S波发展至不稳定态,引起在下表面的转捩位置在0°~4°工况时随迎角增加向前缘移动,在6°工况时向下游移动,表现出复杂的变化关系。 图15 CRM短舱转捩位置随迎角变化Fig.15 Variation of transition position of CRM nacelle with angle of attack 总体而言,在小迎角变化范围内,短舱表面上的压力分布出现较大的变化,逆压梯度出现变化,eN转捩预测方法对逆压梯度的小幅度变化反应敏感,但是转捩位置的变化范围仍在5%短舱长度范围内。 图16 不同迎角下CRM短舱各截面压力分布Fig.16 Pressure distribution of each cross-section of CRM nacelle with different angle of attack 图17 短舱前缘压力梯度和转捩位置随迎角变化Fig.17 Variation of pressure gradient and transition position of naceller leading edge with angle of attack 自由来流马赫数、雷诺数、湍流度以及迎角均对所研究短舱的转捩位置有一定影响,具体变化情况如下: 1) 随着马赫数增加,短舱外表面吸力峰值下降,激波位置向后移动,逆压梯度减小,转捩位置后移。随着雷诺数和自由来流湍流度增加,短舱各截面的压力分布几乎不变,转捩位置更靠近唇口。 2) 随着迎角增加,短舱外表面迎风区吸力峰值下降,压力梯度增加,但压强变化量变小,转捩位置向上游移动(压强变化量特别小的工况除外)。背风区吸力峰值增加,压力梯度减小,转捩位置向下游移动。 3) 在所研究的工况下,马赫数和迎角带来的压力梯度变化明显,引起转捩位置发生变化;而雷诺数和湍流度在高雷诺数工况下影响相对较小,转捩位置的移动不超过5%短舱长度。因此在设计阶段,对保持层流设计来说,要尽量避免较大的逆压梯度,保持顺压梯度。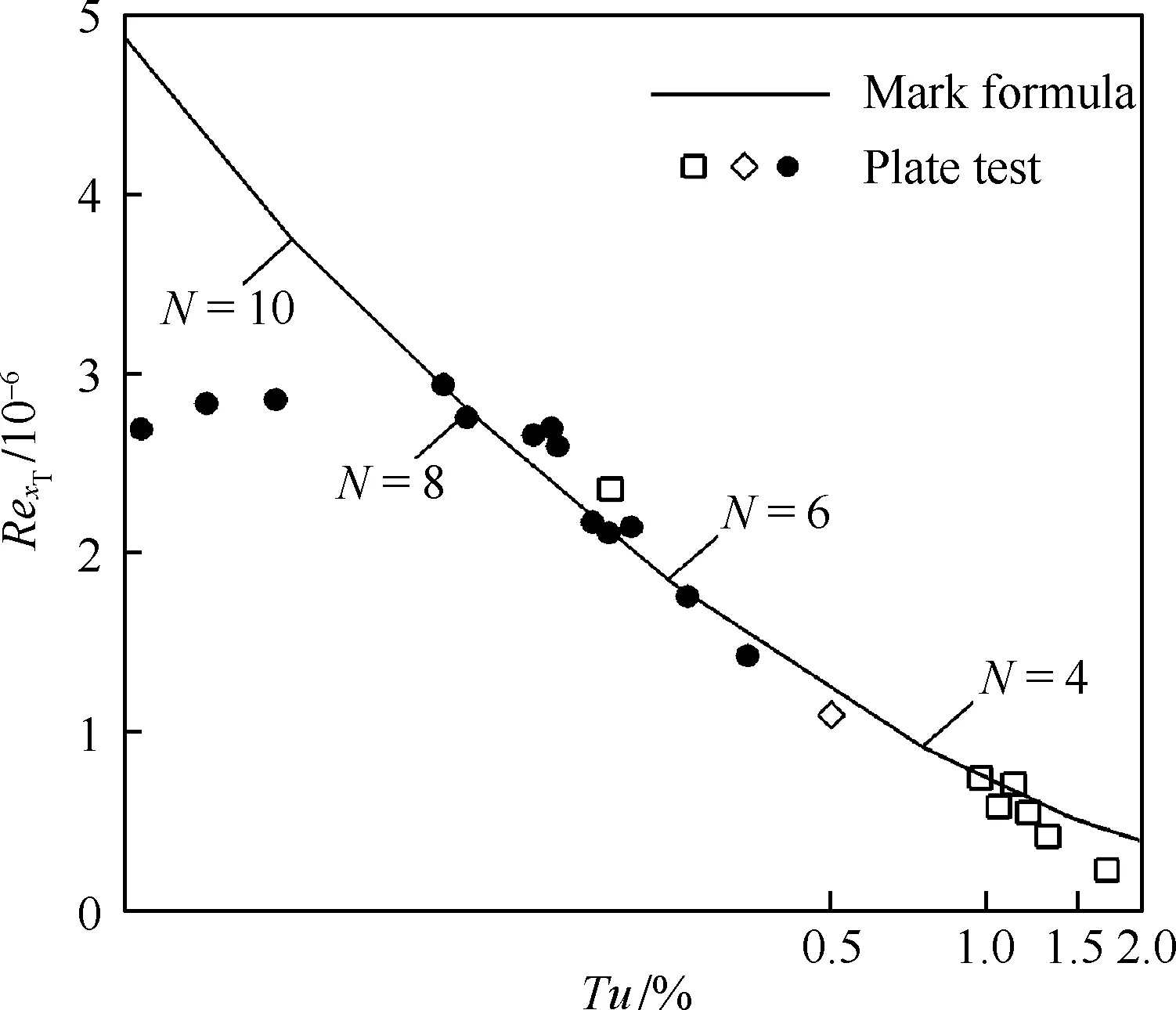
2 算例验证
2.1 数值方法准确性验证
2.2 网格收敛性验证
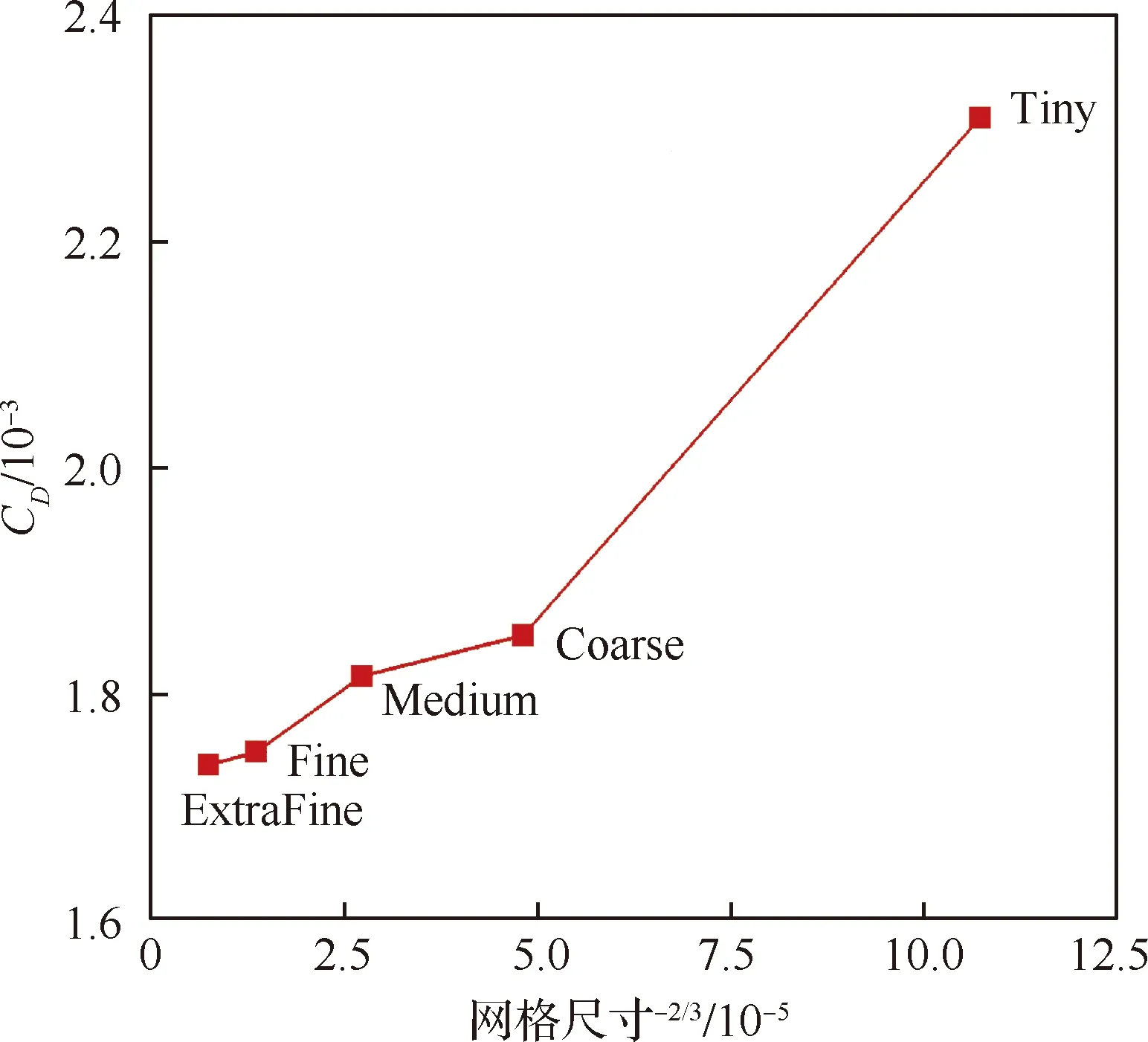
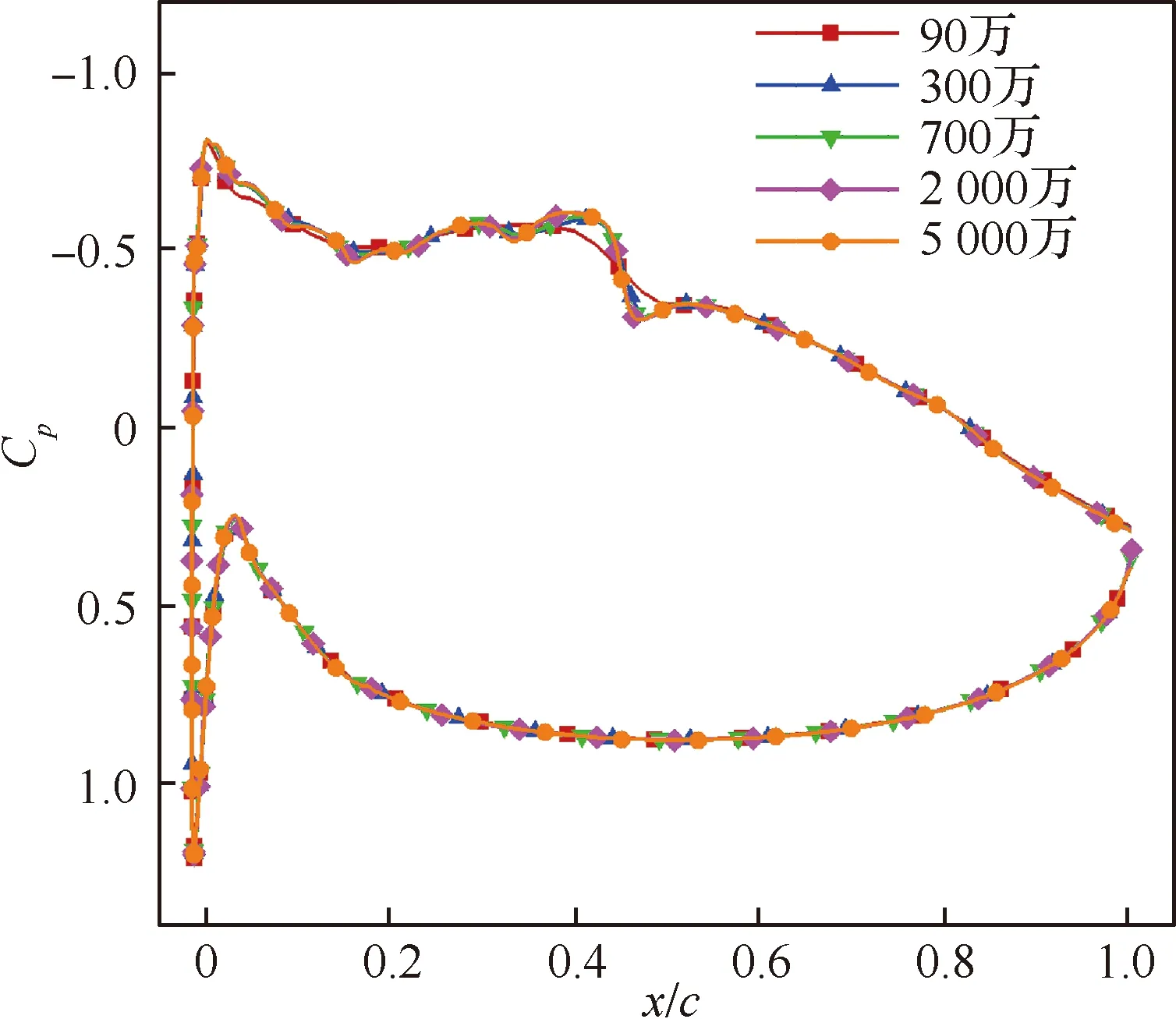
3 短舱层流转捩影响因素分析
3.1 变马赫数分析
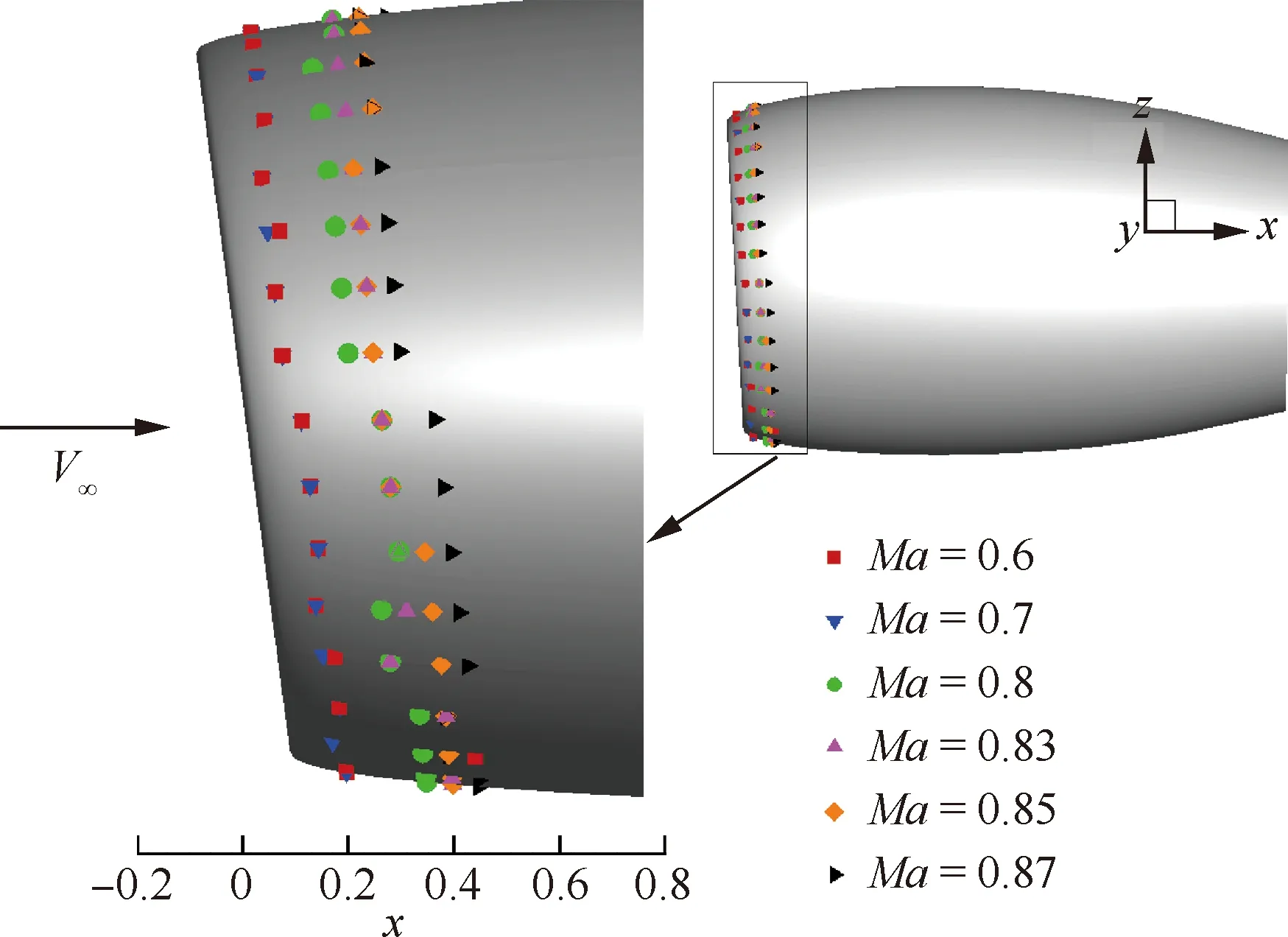
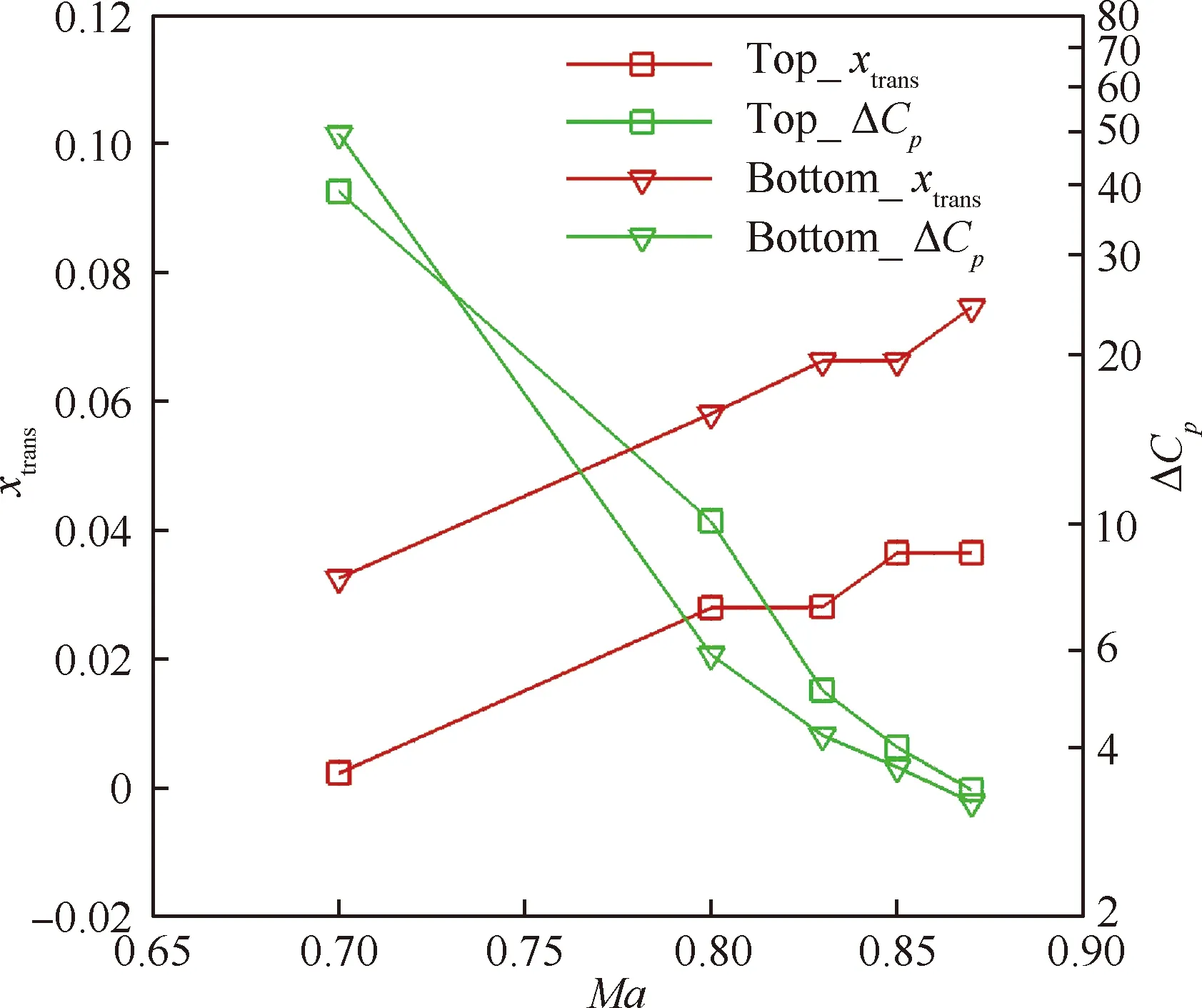
3.2 变雷诺数分析
3.3 变湍流度分析
3.4 变迎角分析
4 结 论
