例题教学中的“变脸”艺术

张孝波

摘要：随着新课改的推进，初中数学课程改革朝着教学的高效性和科学性进步。在初中数学课堂中，教师为了保证教学的高效性，需特别注重培养学生举一反三的自学能力，即教会一道题，会做一片题。这就要求教师在例题讲解中，需要拓展延伸，即所谓的“变脸”艺术，以点带面地将一道例题的全部变式一网打尽。

关键词：初中数学;例题变式;新课改;举一反三

初中数学相对于小学数学来说，开始向综合性方向前进，相关知识的题目量变大，相关知识的应用方式变化多端。许多学生也常常会为此烦恼，碰到初中数学学习的瓶颈，这正是因为初中数学需要迁移能力。迁移能力首先源自于对基础知识的把握，在正确把握了基础知识之后，总结相关规律，才能更好地发挥和把握出题者的意图，从而获得遇题即可开始解答的熟练程度。教师也要在讲解过程中刻意地去训练学生的这种举一反三能力。本文将举例说明这种举一反三式的“变脸”艺术。

一、总结“小定理”

应对初中数学题目变式繁多的问题，作为教师，我们不妨给学生降低难度门槛，给学生总结一些课本上没有的小规律，这些小规律，也是一些小定理，虽然课本上没有总结过，但是在平时我们教学中频繁遇到，每次都让学生自己去证明，固然会浪费大量时间。通过总结这些规律，我们不仅可以提高教学效率，也可以提高学生的学习效率和做题效率。

这些小定理，有的可能被作为口诀记忆，有的可能取了一些好听的小名字。例如我们常说的等角对等边就是个经典例子，等腰三角形能推出其两个腰相等，也能推出其两个腰对应的角相等，反着推也可以，三角形的两个边相等，能推出其是等腰三角形，三角形的两个角相等，也能推出其是等腰三角形，所以我们就有三角形的两个角相等，其对应的边也相等，三角形的两个边相等，其对应的两个角也相等。这些话说起来，很容易将人绕晕，归结起来就是两句话，等角对等边，等边对等角。有些学生害怕这些绕来绕去的定理公理，不妨就这种简单易记的语句方便他们记住，这是他们应对变脸例题的法宝之一。

又例如，我们总结的“看见中线延长一倍”，之所以要说这句话，不是仅仅让学生念口诀，而是希望他们知道这句话的目的。在几何证明里，中线出现频繁，一旦出现中线，就已经有了两个对等的边了，延长一倍之后，立刻会出现一副对顶角，和另一组对等的边。如此一来，我们便快速构造出来了一个全等三角形，这才是这个定理总结的意义所在。至少，要让学生先记住这句话，对于那些基础不扎实的学生，记住这些，就是他们能够学会举一反三的第一步。

二、联想迁移

通过总结一些小结论，使得学生缩短脑回路。即见到特定的条件，便立刻想到相应的结论，从而，读到题目的某些条件时，脑海立马浮现出结论，相当于题目率先就告诉你结论了。实际上，许多题目都是这种小结论的变体，有些可能是这些小结论的合体。如果教师在平常教学中，注意提醒学生总结这些小定理，那么教学的效率便会逐渐提高了。

但是例题的变脸其实也不仅仅是这些现成的东西，还有很多是需要稍微动脑的迁移。比如，关于圆的切割线定理。切割线定理本身没有在教材中出现，但是在初三，这一定理反复出现。由切割线定理延伸出来的还有切线定理、割线定理。这三个定理都可以独自证明（利用相似），也可以相互证明。切割线定理可以说成，同一点引出的切线和割线，切线段长的平方等于割线与圆交点的两条线段长乘积，它的证明可以通过先证明两个三角形相似得到。

那么割线定理可以借切割线定理证明，即过一点作一条切线和两条割线，通过切线过渡，证明两条割线的比例关系，这就是知识的迁移应用。同样，为了培养学生的迁移能力，可以让学生试着用另外一种方法去证明，即证明两个三角形相似。

三、应用举例

接下来，本文举出一个实战例题：

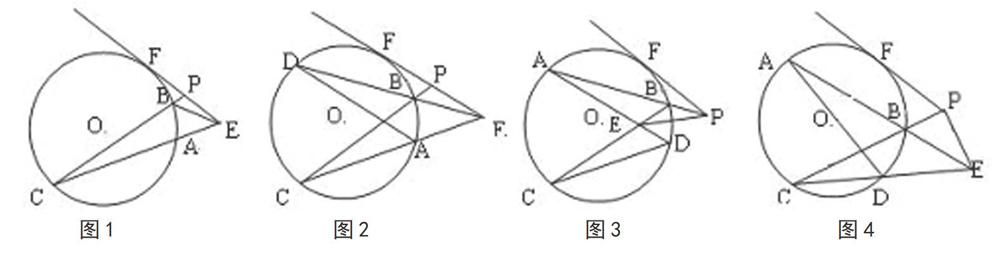
如图，首先来看图1，EF是圆O的切线，F是切点，P是切线上一点，EC是圆O的割线，AC都是割点，∠PBE=∠PEC，请证明：PF=PE。

这道题，要证明PF=PE，可能难倒一些学生。证明相等，很多学生会想方设法构造全等三角形。又或者作各种辅助线。会想到证明P是EF的中线，不妨延长一倍等等，其实都不对。如果对切割线定理熟悉的话，其实这题可以将证明相等转化到证明相似。

根据切割线定理，我们有PF2=PB·PC，下面证明PE2=PB·PC就可以得到PF=PE。而证明PE2=PB·PC的方法也不难，根据条件∠PBE=∠PEC得到△PBE与△PEC相似，由比例交叉相乘即可得到PE2=PB·PC。

这道题目体现了例题讲解中的举一反三的能力迁移，如果将这个题目变换一下，变成图2，题设变为：

如图2，EF、EC分别为圆O的切线、割线，F是切点，弦 AD//EF，ED交圆O于B，弦CB的延长线交EF于P，请证明证：PE=PF。

其实，虽然条件变了，但是这道题的基本思想不會改变，仍然是联合相似三角形的比例以及切割线定理进行解答。只不过这里改为利用平行找到角相等，从而证明△PBE与△PEC相似。

图3、图4分别是其它的变式，思路基本相同，不再赘述，在教学时可以让学生仿照前例，自行解答。

图3中，弦AD与CB相交于E，P为AB延长线上一点，PE//CD，PF为圆O的切线，F是切点，要求证明：PE=PF。

图4中，AB和CD两弦的延长线相交于圆外一点E，PE//AD，PE交BC的延长线于E，PF是圆的切线，F是切点，要求证明：PE=PF。

四、总结

把握例题讲解中的“变脸”艺术，实际上就是要让学生学会迁移应用，保证学生的知识实现模块化，即学生将一个一个熟悉的知识点串联起来，将特定的例题总结成小定理，然后再进行联想迁移，不管遇到什么样的例题变式，都可以分步解决。在教学中注重培养学生这种举一反三、迁移应用的能力，将大大提高教学效率。

参考文献：

[1]费丽超.学习迁移理论在初中数学教学中的应用分析[J].课程教育研究，2019（14）：141-142.