近五年高中数学教与学“理论”研究的回顾与反思

【摘 要】 对2014～2018年间人大复印资料《高中数学教与学》“理论”栏目转载的77篇论文从作者属性、研究方法、研究重点和热点三个维度进行内容分析可知：作者属性呈现出高校引领性、研究独立性、核心群体稳定性的特点;研究方法表现出“重理论思辨，轻实证研究”的异化现象;但历时变化趋势反映出高中数学教与学“理论”研究会适时而变，数学教育研究前景可观. 数学教育发展问题、数学课堂教学问题、数学学习问题、数学文化教育问题和数学核心素养问题是近五年高中数学教与学“理论”研究的重点与热点. 明晰研究问题与研究方法的共生关系、加强教学实践的理论性反思和注重理论的实践性解读是未来“理论”研究的发展方向.

【关键词】 人大复印资料;高中数学;理论研究

1 问题提出

郑毓信曾于“未来十年中国数学教育展望”学术研讨会大会报告中提到：“中国数学教育理论研究的当务之急应当是大力加强理论学习和关注现实，理论的多元化将有益于我们更好的了解数学教育的整体发展”[1].随着“立德树人”根本任务的明确、“中国学生发展核心素养研究”成果的發布和新版《普通高中课程方案》、《普通高中数学课程标准》的颁行，高中数学教育教学改革已迈入深化阶段. 所以，有必要对过去高中数学教与学“理论”研究进行回顾与反思. 正如美国新泽西州拉特格斯大学Daniel Tanner所言：“现在的‘理论知识毕竟是过去实践经验的结果，如果现在要比以往做的更好，就需要加强对先辈们的贡献进行理解和依赖”. 已有研究主要聚焦于《高中数学教与学》年度载文的梳理与解读[2]，但鲜有对“理论”栏目进行历时研究分析. 为此，本研究选取2014～2018年间人大复印资料《高中数学教与学》“理论”栏目转载论文为研究对象，探讨近五年高中数学教与学“理论”研究的作者属性与研究方法有何特征以及这些研究成果关注了哪些重点和热点问题.

2 研究过程与方法

采用人工方式将人大复印资料《高中数学教与学》2014～2018年间的60本样刊按年度和月份次序进行整理，再依次复印每期“理论”栏目下的文章，共收集77篇论文. 这77篇论文是围绕高中数学教与学的基本问题、热点问题、前沿话题及争鸣话题而展开研究的最新成果，是从28种教育类学术刊物中筛选出选题新颖、研究规范、结构完整、逻辑严密的优秀论文. 这些文章具有基础性、权威性、专业性、导向性等特征，当属高中数学教与学“理论”研究的重中之重，也确保了文献来源的信度和文献研究的价值.

根据上述两个研究问题，采用内容分析法，借助SPSS19.0软件对近五年高中数学教与学“理论”研究论文的作者属性、研究方法等确定性顺序变量进行量化统计，分析其基本特征与变化趋势;再反复研读这些论文，按照研究向度和学科视点进行归类分析.

3 研究结果与分析

3.1 作者属性分析

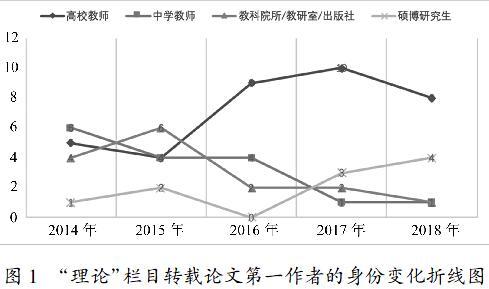
其一，第一作者身份属性. 统计得知，77篇“理论”研究论文的第一作者身份有高校教师、中学教师、教科院所等研究员及硕博研究生四种类型. 高校教师（36篇）几乎占领了半壁江山，比例为46.75%，成为高中数学教与学“理论”研究的主力军;中学教师（16篇）和教科院所等教研员（15篇）次之，两者所占比例相当，分别为20.78%和18.48%;数学教育领域的硕博研究生（10篇）贡献最少，约为12.99%. 但从近五年的变化趋势来看（见图1），高校教师或许仍是高中数学教与学“理论”研究的领头羊，发挥着专家引领作用;硕博士研究生群体呈现递增趋势，将成为“理论”研究的新生力量;而处于“中间地带”的中学教师和教研员呈现递减趋势，但有调查发现，中学数学骨干教师科研能力较为可观[3]，与递减趋势相悖的原因或许是中学教师或教研员还缺乏对教学实践问题的理论性反思.

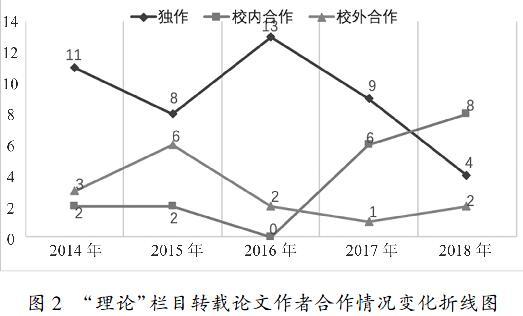
“理论”栏目转载论文第一作者的身份变化折线图其二，作者群体合作情况. 统计得知，77篇“理论”研究论文有45篇为独立作者，约占六成，其中2016年度共转载15篇论文，就有13篇为独立作者;有18篇为校内师生合作和同事合作，约占23.38%;还有14篇为跨校合作，约为18.18%. 但从近五年的变化趋势来看（见图2），自2016年“中国学生发展核心素养研究”成果的发布，数学教育研究“单打独斗”的情况随之减少，新时代倡导的“合作共赢”理念将影响校际教师教研合作共同体的形成.

“理论”栏目转载论文作者合作情况变化折线图其三，高产作者分布. 统计可知，77篇“理论”研究论文共涉及60位第一作者，其中有50位作者分别被转载1篇，有5位作者分别被转载2篇，有5位作者分别被转载3～4篇不等，这也间接性的反映了高中数学教与学“理论”研究的群体面较为广泛. 转载3篇及以上的5位作者被称为高产作者，他们均为高校教师. 现从研究内容的关注点和个体研究的活跃度两方面管窥这5位高产作者的基本特征.

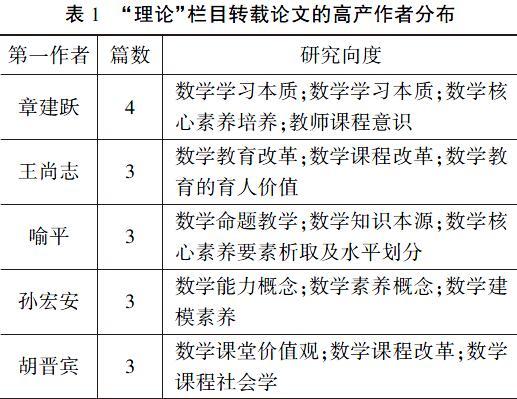
研究内容的关注点主要从近五年5位高产作者被转载的“理论”研究论文的向度中体现. 文献分析可知，章建跃主要从数学教育的本质视角探讨数学学习、数学教学等问题;王尚志主要从教师角度探讨数学教育改革和学科育人问题;喻平主要从心理学角度探讨数学教学问题以及从数学知识角度探讨数学核心素养问题;孙宏安主要关注数学概念分析问题及数学建模素养问题;胡晋宾主要关注数学课程和教学问题. 具体如表1所示.

以上从作者属性对高中数学教与学“理论”研究进行多方面审视，其结果与彭上观对《数学教育学报》论文高频作者的特征研究[4]较为相似，也进一步说明了我国数学教育领域出现的“高校引领性、研究独立性、核心群体稳定性”特征还较为突出，但从近五年高中数学教与学“理论”研究的变化趋势来看，这种现象将会适时而变，数学教育研究将前景可观.

3.2 研究方法分析

论语有言“工欲善其事，必先利其器”，“事”如研究，“器”如方法. 研究方法之于学术研究至关重要，它取决于研究问题，制约着研究结论，决定着研究进展. 按照姚计海等人對教育研究方法的分类[5]，高中数学教与学“理论”研究论文采用思辨研究、质性研究、量化研究、混合研究等方法的数量分别为：64篇、6篇、4篇、3篇，分别占比83.12%、7.49%、5.19%、3.90%. 总体看来，思辨研究仍是“理论”研究的主要方法，高达83%. 这一结果与熊斌等人调查《数学教育学报》（2011～2015）刊载论文所采用的研究方法的结果较为相似[6]，均表现出“重理论思辨，轻实证研究”的异化现象. 但从近五年四种研究方法运用的变化来看，高中数学教与学“理论”研究的方法将由单一思辨向多元混合发展，具体如图3所示.

图3 “理论”栏目转载论文的研究方法变化图由图3可知，《高中数学教与学》“理论”栏目转载论文采用思辨研究方法呈现出逐年递减趋势;即使质性研究、量化研究及混合研究等范式研究成果总量较少，也呈现出“雨后春笋”式的萌发态势. 那么，这些实证研究论文具体采用了什么研究方法，关注了哪些问题？值得特别关注.

6篇质性研究论文，都关涉高中数学教与学的本质问题. 有4篇采用访谈法，其访谈对象分别是齐民友、史宁中、张维忠、数学教师发展指导者，主要探讨数学教育改革、数学核心素养的本质、数学文化与数学课程改革以及信息技术对数学学习的影响等问题;另有2篇采用文本分析法，主要探讨我国数学家对数学课程改革的认识和美国《数学教师》杂志数学文化活动类论文的主题分布等问题.

4篇量化研究论文，有两种类型，一是简单描述性统计和差异性分析，如乔爱萍和王发成采用问卷的方式调查高中数学教师对数学文化教育的认识与实施情况;二是关联性统计分析，如张淑梅等人使用聚类分析、广义相关测量、因子分析等方法对六个数学核心素养进行相关性分析.

3篇混合研究都是采用定性与定量相结合方式探讨数学核心素养和数学基本活动经验等问题. 如王光明等人综合采用文献研究、专家咨询、测试等方法构建了高中生数学素养的操作定义;郭玉峰等人也综合采用文献分析、调查研究、因素分析、聚类分析等方法划分了数学基本活动经验的主成分和层次水平.

3.3 研究重点与热点分析

3.3.1 聚焦数学教育发展问题

教育的根本在于培养“人”，由知识本位向素养本位的转变凸显出数学教育育人价值的根本变革，这种变革有赖于中国数学教育界的专家引领与推动. 如刘祖希（2014年第5期，简写为2014.5，下同）通过回顾当代中国数学教育发展道路，总结出我国初步形成了“一徐二张”的数学教育流派. 随着“立德树人”的提出，学者们就当下高中数学课程改革发展问题展开了讨论，其代表性观点有三：一是展望高中数学课程改革发展方向. 如王尚志（2015.8）、鲍建生（2018.6）、胡晋宾（2015.10）、俞求是（2014.6）等人从课程教材、教师发展、课堂教学、学习材料等方面对高中数学教育进行了展望. 二是重新定位数学育人价值. 如史宁中（2017.7）认为数学教育的根本在于培养学生的数学直观;王尚志（2018.12）认为数学的育人价值在于促进人的理性思维、科学精神、严谨求实态度、数学建模素养、创新意识和能力以及学会学习的形成与发展. 朱哲（2017.10）也持类似的观点，认为培养学生数学学科学习力至关重要. 三是对数学资优教育的博弈. 相较于大众数学教育，数学资优教育一直是国内数学教育界争鸣不断的话题. 高中数学教育要落实基础性、发展性、选择性的课程性质，理应思考数学资优教育问题. 张倜等人（2017.9）总结了国外数学英才教育研究在选拔方式、项目培训、课程设置等理论和实践层面取得的成果，启示我国数学英才教育研究需要在课程和教师两方面加以改进. 鲍建生等人（2018.6）认为不论资优教育，还是大众教育，最重要的是让学生真正爱上数学.

“四基”已俨然成为中国数学教育独具特色的“名片”，历来备受关注. 五年来，学者们对“四基”问题进行了深化研究. 在基础知识上，于波等人（2017.2）认为除数学公式、定理、概念等显性知识外，数学缄默知识同等重要，它关涉学生对数学知识的理解与建构，其外部表征有助于学生数学思想、数学思维的发展和利用. 在基本技能上，孙宏安（2016.3）系统分析了数学能力概念的内涵与外延，指出数学能力的内涵有心理学和数学活动两种视角的表述，外延也有“由能力出发进行数学限定得出的各种数学能力”和传统的“三大能力+解决问题能力”两类表述，数学能力概念虽然有不同表述，但其内涵与外延的对应关系具有本质一致性. 在基本思想上，马文杰等人（2018.3）认为数学思想方法具有概括性、深刻性、内隐性、层次性、发展性、迁移性、启发性、广泛应用性等基本特征. 数学思想方法蕴含于具体的数学知识之中，二者具有密不可分的联系. 随着信息技术与数学课程的深度融合，将信息技术融入数学教学对发展学生数学思想具有重要价值. 如刘咏梅（2017.5）等人以抽象、推理及模型3种数学思想为例，结合案例分析了信息技术融入数学教育将有利于展现抽象思维的理性文化特点，提升对数学对象关联性的理解;有利于增强归纳推理的客观性和演绎推理的深刻性;有利于为建模和用模解决问题提供丰富素材. 在基本活动经验上，郭玉峰等人（2017.10）通过实证研究划分出数学基本活动经验的4个主成分，分别为归纳概括、类比推广、数学表达、证明，以及每个主成分所对应的3个层次水平.

3.3.2 重视数学课堂教学问题

理解数学是教师教学的基本前提，当下教学中所暴露的问题，主要源于教师教学观的缺失. 近五年高中数学教与学“理论”研究主要从应然层面探讨了教师理解数学的观念问题. 如严亚强（2016.6）建议教师应该学点数学教育哲学;章建跃（2016.9）认为教师应增强课程意识. 李祎（2014.10）、李昌观（2017.8）、张曜光（2018.11）等人主要从数学教育的整体性和数学知识的联系性等方面强调教师理解数学的根本之道.

作为中介的教学模式在教学理论与教学实践中起着重要的作用，当前关于高中数学教学模式的研究主要有两个方面，一是问题教学模式的应用研究. 问题是数学的心脏，自20世纪80年代以来，问题教学在数学教学中得到广泛应用. 如孙福明（2015.5）、朱占奎（2014.8）等人结合案例阐述了“问题引领课堂”的重要性. 二是数学教学模式的问题研究. 傅海伦等人（2014.2）从理论研究、实践研究和课堂选用三个方面分析了数学教学模式存在的主要问题，启示研究者在构建新型数学教学模式时要注意研究方法的科学性;实验者在推广新型数学教学模式时要注意对一线教师的培训与指导;一线教师在运用数学教学模式时，要注意更新观念，形成正确的数学教学模式观. 李建军（2015.9）也具体分析了数学学案导学教学模式在高中数学教学中存在学案的强化与教案的虚化、预习环节的巩固与学习负担的增加、学生主体性的凸显与教师主导作用的缺失的矛盾问题.

数学课堂教学变革反映了课程改革是否实施的依据，“什么样的课堂教学才有价值”一直是教育改革热议的话题. 五年来，大多数学者就数学课堂教学价值标准问题进行了多方面的探讨，主要有四种视角的认识. 一是课程视角. 如李祎（2015.3）认为高水平数学教学应在教教材中显性知识的同时，更要深度挖掘和解读教材中的隐性知识，这些隐性知识就是数学的本质（概念、结论、方法）、过程、思想和结构;同样，曹广福（2016.7）认为要批判性的看待数学教材，数学课堂教学不能拘泥于教材，应抛弃充斥于教材中的伪问题，以真正的问题驱动课堂教学，通过引入思辨因素以增强课堂的弹性. 二是知识视角. 如章建跃（2017.9）认为应结合具体内容从数学知识的发生发展过程，特别是如何发现和提出数学问题、获得数学对象的角度进行教学. 三是学生视角. 如章建跃（2015.11）、朱哲（2015.7）、李建军（2015.6）、孙福明（2014.3）、朱占奎（2014.8）等人认为数学教学的目的是为了发展学生的数学思维，学会数学的思考;何勇（2014.8）还从概念课、原理课及解题课3个模块具体阐述了数学课堂教学还应兼顾学生数学素养的差异. 四是哲学视角. 如俞昕（2014.2）和胡晋宾（2015.5）认为数学课堂教学应体现目标达成、主体互动、知识呈现、教学环节、知识生成的和谐统一以及在數学味、教学味和文化味之间寻求一种动态平衡.

3.3.3 把脉数学学习问题

数学教学的根本指向在于造就学生良好的数学认知结构. 文献分析可知，近五年主要围绕数学学习CPFS结构的教育价值进行了探讨. 如喻平（2016.5）认为学生数学学习中特有的认知结构是由概念域、概念系、命题域、命题系组成，CPFS结构体系是学生头脑中内化的数学知识网络，对学生的数学理解、学习迁移、探究问题能力、解决问题能力产生正面影响. 谢全苗（2016.5）在CPFS结构理论基础上，探讨了数学教学应从数学知识的生长点出发，按数学知识的自然生长机理设计教学，使得学生的数学认知结构随着数学知识、方法的生长而共同生长.

适切的学习方式有助于学生数学成就的表现，但当前出现的数学学习方式也存在诸多问题. 如刘清昆（2018.9）结合实践探索发现混合式学习存在认知理念故步自封、网络学习资源供给侧失衡、实践操作囿于简单思维等问题，针对这些问题，阐述了高中混合式学习应在网络学习资源建设、模式创新、课型实践机制方面加以改进. 学生数学核心素养的落实有赖于数学学习方式的变革，迈向学生主体的深度学习、学会学习. 如徐章韬（2017.12）认为要达成“以学定数”，凸显数学学习理论之用，需深化对教学方式和方法的认识，鼓励学生多种思维能力协同发展;安排进阶式教学序列，塑造学生良好的认知结构推动理解;根据知识的层次体系施教，推动学生情意系统发生变化走向“乐学”. 作为数学教与学过程的媒介，信息技术越来越多地应用于数学教育领域，信息技术与数学课程与教学的深度融合，终究给学生数学学习带来了哪些影响？毛耀忠等人（2018.5）对42位数学教师发展指导者的访谈发现：信息技术的应用形式、应用功能、课堂规范、身份认同等因素对数学学习产生重要影响，启示数学教育工作者在实践过程中应创造性地使用信息技术、重视信息技术支持下的数学课堂规范塑造、建构学生在信息技术支持下的数学学习自我身份认同、优化信息技术与数学学习融合的外部环境.

3.3.4 关注数学文化教育问题

数学是一种文化，数学教学是一种文化实践的教学[7].五年来，主要从两个方面对数学文化教育问题进行探讨. 一是学理分析. 如殷玉波（2014.9）认为数学具有真善美的欣赏性;黄友初（2014.12）诠释了数学文化的教育性和教学性. 数学文化写入课标、进入高考以及对数学教科书编写产生重要影响，足以见得数学文化与数学课程改革的深层关系. 如史嘉（2018.4）通过对话形式对张维忠教授就“数学文化与数学课程教学改革”问题进行了深度访谈. 那么，数学教育教学过程中，应如何实施数学文化教育呢？王生（2014.6）从数学家徐利治的数学教育观中指出当前数学教学应该重视和加强数学文化内涵、数学思想观念、数学素养、优秀人格品质等方面的研究;张奠宙（2015.4）则认为数学课堂教学应注重弘扬中华传统文化. 二是问题研究. 自高中课标实验版实施以来，理念与实践的脱节仍是当前数学文化教育亟待解决的问题. 如黄友初（2014.12）、乔爱萍（2016.1）、王发成（2017.3）等人通过实证研究得出高中大部分教师在观念与行为上不重视课堂教学渗透数学文化，主要是教师自身缺乏数学文化素养以及教学评价机制的影响. 因此，促使数学文化教学性的理性回归，需要从内部与外部两方面加以引导，首先教师自己要养成文化自觉的意识;其次还应从外部加强数学文化与数学教育的培训、开发数学文化融入数学教学案例、营造数学文化课堂评价机制的生存空间.

3.3.5 热议数学核心素养问题

随着高中数学课程标准的修订与颁布，数学核心素养一度成为当前讨论最热的话题. 总体看来，学者们主要围绕数学核心素养的内涵、要素、体系建构、培养策略等方面进行多样化的探讨，虽然没有达成统一的共识，但是也丰富了人们对数学核心素养的理解.

一是对数学核心素养内涵的认识. 史宁中（2017.6）认为数学核心素养的本质是培养学生“三会”. 这种描述性定义为其他学者从构成要素角度认识数学核心素养的内涵提供了思考空间. 如王光明（2016.11）认为高中生数学素养是对数学内容的融通素养，是将现实问题转化为数学问题的建模素养，是用数学的眼光看世界、数学的思维分析世界、数学的语言诠释世界的数学能力素养，并从数学内容、现实情境、数学过程三个维度构建了高中生数学素养的可操作定义. 吕世虎（2017.12）认为数学核心素养是个体从数学的角度观察事物，并借助数学知识与思想方法解决数学学习或者现实生活情境中相关问题的综合能力以及个体所持有的数学情感态度、价值观等.

二是对数学核心素养构成要素和体系建构的认识. 孙宏安（2017.1）、华志远（2016.9）、武小鹏（2018.10）等人主要对高中数学课标划分的六大素养进行了重新理解与解读;还有一部分学者对这种划分进行了“再创造”，体现了对数学人文价值和理性精神的重视. 如何小亚（2016.10）反思六大素养的内涵与表述，提出数学核心素养应当由数学化、数学运算、数学推理、数学意识、数学思想方法、数学情感态度价值观组成. 喻平（2017.4）则在六大素养基础上从实证研究角度析取出数学核心素养还应包含问题解决能力和数学文化品格. 六大素养在逻辑上构成一个有机整体，相互联系、相互促进. 如张淑梅（2018.2）对六大素养之间的相关性进行分析，认为数学素养可以分为三类：数学抽象、逻辑推理、直观想象、数学运算作为基本数学素养为一类，数学建模与数据分析各成一类. 吕世虎（2017.12）还构建了数学核心素养的数学双基层、问题解决层、数学思维层、数学精神层的体系结构.

三是对数学核心素养培养的认识. 最近三年，关于学生数学核心素养的培养问题得到了诸多学者的重视，如吴新华（2016.12）、孙成成（2017.5）、朱立明（2018.7）等人通过对数学核心素养的认识与理解，阐述了多样化的培养策略，在此不一一展开. 在探讨培养路径与落实问题上略显经验化，甚至还有研究将六大素养分割开来从教学案例中思考素养落地问题，这些教学实践还需加强理论性解读.

4 反思

高中数学教与学“理论”研究在数学教育发展问题、数学课堂教学问题、数学学习问题、数学文化教育问题和数学核心素養问题等方面得到积极探讨，不仅开阔了数学教育研究者和实践者的理论视野，还夯实了数学教育研究领域的理论基础. 但同时还应注意到，研究群体的高校引领性和独立性以及思辨研究方法的推崇性或许成为高中数学教与学“理论”研究的藩篱，为此，应反思如下两个问题.

4.1 明晰研究问题与研究方法的共生关系

从理论的界定来看，国际数学教育委员会前秘书长Mogens Niss从数学角度指出：“理论是一个有结构的、连贯的关于概念和论点的网络. 其中论点是由基于实证数据、材料或者逻辑推理得到的简单论点构成”[8].所以，高中数学教与学“理论”研究方法理应在思辨与实证之间取得平衡. 同时，还应关乎所要研究的问题，采取适切的研究方法，因为研究方法是根据具体研究问题的确定而得到选择. 例如，在数学文化教育问题上，目前对数学文化的概念尚未统一，但数学文化融入数学教育教学已成当下热点之一，这种追认式的概念迷思或许影响着数学文化教育的发展. 因此，有必要从内涵与外延阐述数学文化的概念及其二者之间的关系;同时，有待进一步构建评价指标体系，使之数学文化教育教学的评价问题得以实证化. 再如，核心素养导向下的深度学习有赖于深度教学的引领，那么，什么样的课堂教学可谓深度教学，就需要通过课堂观察、凯利方格等实证方法加以研究，等等.

4.2 加强教学实践的理论性反思和注重理论的实践性解读

从教与学的文化属性来看，理论与实践是一种文化性同在，其关系是文化关涉的文化事件与文化现象[9].所以，要想超越高校教师与一线教师之间形成的理论与实践的限度，理解理论与实践的文化同在性至关重要，或将 “理论”研究朝向“理论的实践性解读”和“教学实践的理论性反思”发展[10].例如，在培养学生数学核心素养问题上，应注重理论的实践性解读，进一步将发展学生数学核心素养的理念真正落实到课程、教科书、课堂教学以及学业评价，使之成为可操作、可测评、可诊断的有机体系，并从实践的角度对此作出分析与解读. 再如，在数学课堂教学价值观问题上，应加强教学实践的理论性反思，目前对数学课堂教学价值标准问题的探讨多源于一线教师的教学主张，进一步将教学实践的总结与反思从更为一般的角度进行理论分析与思考，从而引出具有更大普遍性的问题、启示与教训，使之形成教师的教育智慧.

参考文献

[1] 郑毓信.数学教育的理论建设[J].数学教学，2014（7）：1-5.

[2] 张定强，闫佳洁.高中数学教育研究的热点与重点——对2017年度人大复印报刊资料《高中数学教与学》转载论文的分析与展望[J].中学数学，2018（5）：44-49.

[3] 吕世虎，金晶，岳艳萍.中小学数学骨干教师科研现状的调查研究[J].中小学教师培训，2012（4）：37-39.

[4] 彭上观.《数学教育学报》论文高频作者的特征研究——基于1992-2015年载文的实证视角[J].数学教育学报，2017，26（2）：96-100.

[5] 姚计海，王喜雪.近十年来我国教育研究方法的分析与反思[J].教育研究，2013，34（3）：20-24+73.

[6] 牛伟强，张丽玉，熊斌.中国数学教育研究方法调查研究——基于《数学教育学报》（2011-2015）的统计分析[J].数学教育学报，2016，25（6）：88-92.

[7] 张维忠.数学教育中的数学文化[M].上海：上海教育出版社，2011：6-14.

[8] 张舒，曹一鸣.“问题”“理论”与“方法”：如何做好数学教育研究——访国际数学教育委员会前秘书长Mogens Niss教授[J].数学教育学报，2018，27（6）：50-54.

[9] 段兆兵.教学理论与实践关系的文化思考[J].教育理论与实践，2009，29（25）：46-49.

[10] 郑毓信.新数学教育哲学[M].上海：华东师范大学出版社，2016：369-375.

作者简介 汪飞飞（1992—），男，安徽合肥人，博士生，主要从事数学课程与教学论研究.