解析几何测试题A 参考答案
2019-12-06
一、选择题
1.B 2.C 3.B 4.A 5.D 6.B
7.C 8.C 9.A 10.D 11.A 12.B
二、填空题
13.4 14
15.-3 16.a=-1或a=5 2
三、解答题
17.(1)直线2x+y-1=0 与x轴的交点是故p=1。所以抛物线的方程是y2=2x。
(2)设过点A(2,0)的直线方程为l:x=my+2,当m不存在时,直线l与抛物线只有一个交点,故舍去。
当m存在时,联立消去x整理得y2-2my-4=0,Δ=4m2+16>0恒成立。设B(x1,y1),C(x2,y2),则y1+y2=2m,y1y2=-4。所以(x2,y2)。
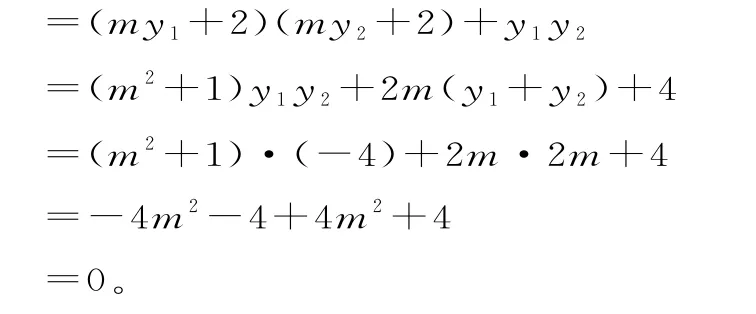
所以OB⊥OC,所以∠BOC=90°。
18.(1)因为C2:y2=2px的焦点F的坐标为由点F到直线x-y+1=0 的距离为得
因为p>0,所以p=2,所以F(1,0)。
(2)因为F(1,0)为椭圆的一个焦点,所以
因为C1与C2的公共弦长为与C2都关于x轴对称,所以C1与C2的公共点的纵坐标为
联立①②解得a2=9,b2=8,所以C1的。
19.(1)设边界曲线上的动点为P(x,y),则由|PA|+|PB|=10,可知点P在以A,B为焦点(焦距为2c=8),长轴长为2a=10的椭圆上。此时短半轴的长为b=3,所以方程为考察区域边界曲线的方程为
(2)由于经过P1(-14,-3),P2(-5,9)两点的直线方程为4x-3y+47=0,所以点A(-4,0)到直线P1P2的距离为d=
又经过n年,冰川边界线所移动的总距离为由点A恰好在冰川的边界线上,得解得n=5。
所以经过5年点A恰好在冰川的边界线上。
20.(1)由抛物线的性质,知焦点F到准线的距离为8。
由|MF|=p+|MF|cos 60°,得8=p+4,即p=4,故抛物线C的方程为y2=8x。
(2)焦点F(2,0),由题意知直线斜率不为0,所以设直线l的方程为x=ty+2。
与C的方程联立消去x整理得y2-8ty-16=0。
由韦达定理可得y1+y2=8t,y1y2=-16。
又坐标原点到直线l的距离d=因为所以
当t=0时,取到最小值8,故△AOB面积的最小值为8。
21.(1)由椭圆的定义可知,2a=4,a=2。又因为点上,故,得b2=3,故椭圆方程为(2)设直线l的方程为y1),C(x2,y2),联立直线l的方程与椭圆方程得
当Δ>0时,即m2-4(m2-3)>0,也即|m|<2时,直线l与椭圆有两个交点。
所以k1+k2=0。
