空间几何知识结构与拓展
2019-12-06安徽省利辛高级中学
■安徽省利辛高级中学 胡 彬
一、知识结构框架

二、结构分析
立体几何研究现实世界中物体的形状、大小与位置关系。通过对立体几何初步的学习,可以帮助同学们以长方体为载体,认识和理解空间点、直线、平面的位置关系;用数学语言表述有关平行、垂直的性质与判定,并对某些结论进行论证;了解一些简单几何体的表面积与体积的计算方法;运用直观感知、操作确认、推理论证、度量计算等认识和探索空间图形的性质,建立空间观念。通过对空间向量与立体几何的学习,可以帮助同学们在平面几何的基础上,运用向量的方法研究基本图形的位置关系和度量关系,体会向量方法和综合几何方法的共性和差异;运用向量方法解决简单的数学问题和实际问题,感悟向量是研究几何问题的有效工具。
本部分一直是高考的重点、难点与热点。一般以基本图形为载体,利用其定义、性质进行判定、计算,或利用空间向量有效研究立体几何相关问题。本部分涉及的数学思想主要为函数与方程思想、转化与化归思想、分类讨论思想。较好地培养了同学们的空间想象能力、推理能力和运算求解能力。考查的核心素养是直观想象、逻辑推理和数学运算。
三、经典例题
典例1(2019 年浙江卷)祖暅是我国南北朝时期的伟大科学家,他提出的 “幂势既同,则积不容异”成为祖暅原理,利用该原理可以得到柱体的体积公式V柱体=Sh,其中S是柱体的底面积,h是柱体的高,若某柱体的三视图如图1 所示(单位:cm),则该柱体的体积(单 位:cm3)是( )。

图1
A.158
B.162
C.182
D.324
解析:由三视图可知,该几何体是一个直五棱柱,由正视图与侧视图可知俯视图(五边形)的参数,即3+2×3+6×6)=27(cm2)。又柱体的高为6 cm,所 以 其 体 积V=Sh= 27 × 6 =162(cm3)。故选B。
点评:三视图问题的常见类型及解题策略:(1)由几何体的三视图还原几何体的形状,要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图。(2)由几何体的直观图求三视图。注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示。(3)由几何体的部分视图画出剩余的部分视图。先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式。
典例2(2019年洛阳第二次统考)在四面体ABCD中,AD⊥平面ABC,AB=,BC=2,若四面体ABCD的外接球的表面积为则四面体ABCD的体积为( )。
A.24 B.12 C.8 D.4
解析:如图2,因为四面体ABCD的外接球的表面积为所以球的半径为又AB=AC=BC=2,所以cos∠BAC所以sin∠BAC=所以△ABC的外接圆的直径为所以O1A=所以球心O到平面ABC的距离OO1=4。又AD⊥平面ABC,所以AD=2OO1=8,所以四面体ABCD的体积为故选C。

图2
点评:(1)解决与球有关的内切或外接的问题时,关键是确定球心的位置,若求内切问题,则球心到各面的距离相等且都为球的半径;若求外接问题,则球心到各个顶点的距离相等且都为球的半径,同时要构造出球心到截面圆的垂线段,小圆的半径和球半径组成的直角三角形,从而利用解直角三角形求出待求量。(2)熟记正方体、长方体、正四面体的内切(外接)球的半径对解答客观题是有很大帮助的。
典例3(2018年全国Ⅰ卷)如图3,四边形ABCD为正方形,E,F分别为AD,BC的 中 点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF。
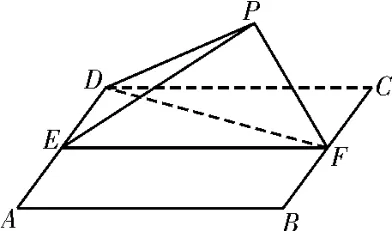
图3
(1)证明:平面PEF⊥平面ABFD;
(2)求DP与平面ABFD所成角的正弦值。
解析:(1)由已知可得,BF⊥PF,BF⊥EF,所 以BF⊥ 平 面PEF。 又BF⊂ 平 面ABFD,所以平面PEF⊥平面ABFD。
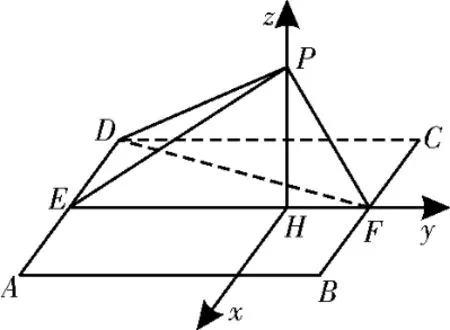
图4
(2)作PH⊥EF,垂足为H,由(1)得,PH⊥平面ABFD,以H为 坐 标 原 点的方向为y轴正方向,为单位长,建立如图4 所示的空间直角坐标系H-xyz。由(1)可得,DE⊥PE,又DP=2,DE=1,所以又PF=1,EF=2,故PE⊥PF,可得则H(0,0,0),为平面ABFD的法向量。设DP与平面ABFD所成角为θ,则所以DP与平面ABFD所成角的正弦值为
点评:(1)平行、垂直关系的证明问题是以空间几何体(主要以柱体和锥体)为载体,通过空间平行、垂直关系的证明进行命题,主要考查公理4及线面(面面)间的平行与垂直的判定或性质定理,常与平面图形的有关性质进行交汇考查。(2)求线面角时,应注意点的坐标的求解的准确性及公式中角的范围为
典例4(2019 年全国Ⅲ卷)图5 是由矩形ADEB、Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连接DG,如图6。

图5
(1)证明:图6 中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
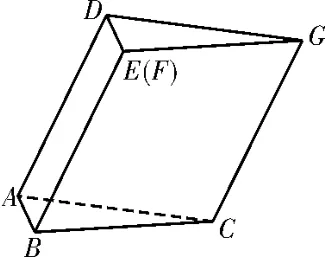
图6
(2)求图6中的二面角B-CG-A的大小。
解析:(1)由已知得AD∥BE,CG∥BE,所以AD∥CG,故AD,CG确定一个平面,从而A,C,G,D四点共面。 由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE。又因为AB⊂平面ABC,所以平面ABC⊥平面BCGE。
(2)作EH⊥BC,垂足为H,因为EH⊂平面BCGE,平面BCGE⊥平面ABC,所以EH⊥平面ABC。由已知得菱形BCGE的边长为2,∠EBC=60°,可求得BH=1,EH=以H为坐标原点的方向为x轴正方向,建立如图7所示的空间直角坐标系H-xyz,则A(-1,1,0),C(1,0,0),G设平面ACGD的法向量为n= (x,y,z),则即所以可取n=(3,6,-又平面BCGE的法向量可取为m=(0,1,0),所以因此二面角B-CG-A的大小为30°。

图7
点评:(1)对于折叠问题,关键是理清折叠前后变与不变的数量关系及位置关系,特别是隐含着的垂直关系。(2)建系时,无明显的垂直关系需要给予证明。
典例5(2019年济南市高三模拟)如图8,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,PA=AB=2,M为 棱PC的中点,E,F分别为棱AB,BC上的动点(E,F与 所在棱的端点不重合),且满足BE=BF。

图8
(1)证明:平面PEF⊥平面MBD;
(2)当三棱锥F-PEC的体积最大时,求二面角C-MF-E的余弦值。
解析:(1)连接AC交BD于N,连接MN。因为底面ABCD为正方形,所以AC⊥BD,AN=CN。又PM=MC,所以MN∥PA。又PA⊥底面ABCD,所以MN⊥底面ABCD。又AC⊂底面ABCD,所以AC⊥MN。又BD∩MN=N,BD,MN⊂平面MBD,所以AC⊥平面MBD。 因为BE=BF,BA=BC,所以即EF∥AC,所以EF⊥平面MBD。又EF⊂平面PEF,所以平面PEF⊥平面MBD。
(2)设BE=BF=x,由题意知,S△CEF=又PA=2,所 以V三棱锥F-PEC=易知当三棱锥F-PEC的体积最大时,x=1,即此时E,F分别为棱AB,BC的中点。
以A为坐标原点,的方向为x轴正方向,建立如图9 所示的空间直角坐标系A-xyz,则C(2,2,0),F(2,1,0),E(1,0,0),M(1,1,1设n=(x1,y1,z1)是平面MEF的法向量,则可取n=(1,-1,1)。设m=(x2,y2,z2)是平面MCF的法向量,则即可取m= (1,0,1),则由图知所求二面角为钝二面角,所以二面角C-MF-E的余弦值为

图9
点评:二面角的求解策略:(1)向量法,又有两种求法:①分别求出二面角的两个半平面所在平面的法向量,利用其法向量的夹角并结合实际图形或法向量的方向确定其二面角的大小。②分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量,显然这两个向量的夹角的大小就是二面角的大小。(2)综合法,根据定义,在图中指(作)出,并给予证明,然后将其纳入可解三角形中求解。
