立体几何“易错问题”归类剖析
2019-12-06江苏省江都中学唐海军
■江苏省江都中学 唐海军
立体几何主要考查空间想象能力(识图、画图、用图、构图)、推理论证能力、运算求解能力、将 “空间问题平面化、模型化和代数化”的转化能力,以及一些重要的数学思想方法的应用。同学们在学习和复习中受认知水平所限,容易出现种种思维误区,本文对立体几何中的易错题归类剖析,给出错因分析和提醒,希望能助同学们一臂之力。
易错1——三视图还原几何体时 “虚实不分,对应不当,不作检验”
例1如图1,网格纸上的小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的体积为( )。
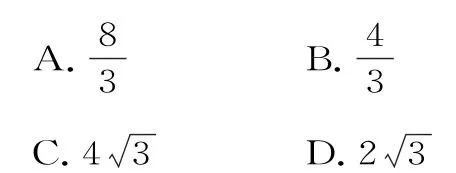
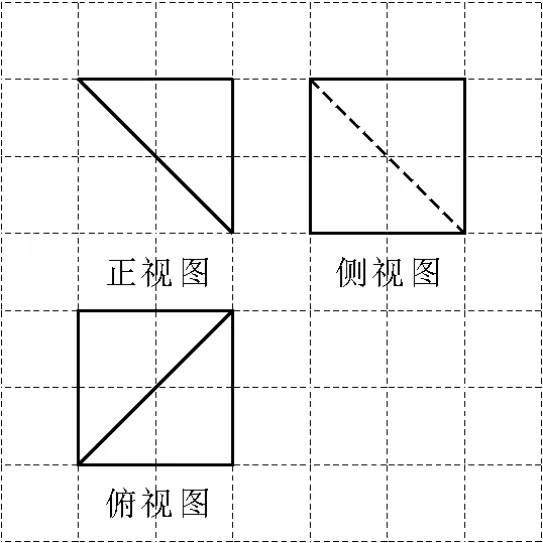
图1
错解:由三视图知,四棱锥的底面为正方形,其边长为2,高为2,则体积故选A。
错因剖析:凑巧蒙对答案,还原几何体时缺少模型化的意识。
正解:由三视图知该棱锥为一个边长为2的正方体中的四棱锥,如图2所示,底面是矩形A1B1CD,宽CD=2,长因为CD⊥平面ADD1A1,所以平面A1B1CD⊥平面ADD1A1,过D1作A1D的垂线D1E,则有D1E⊥ 平面A1B1CD,即 高D1E=所以棱锥的体积V=
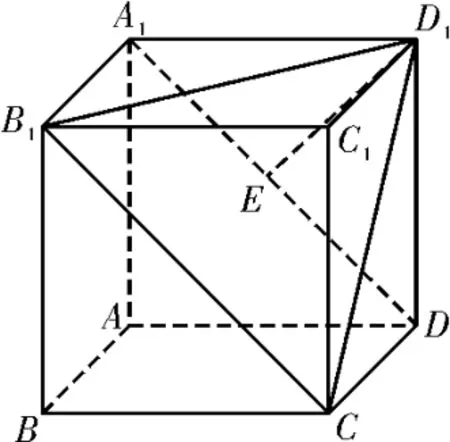
图2
提醒:由三视图还原几何体求体积,要弄清几何体的特征,把三视图中的数据、图形特点准确地转化为对应几何体中的线段长度、图形特点,进而用公式求解。若几何体的三视图中至少有两个视图为三角形,则该几何体为锥体;如果三视图中出现两个或三个矩形或直角三角形,就可考虑以长方体为载体进行视图还原。
易错2——三棱锥体积求解中忽略 “等积变换”
例2如图3,在棱长为5 的正方体ABCDA1B1C1D1中,EF是棱AB上的一条线段,且EF=2,Q是A1D1的中点,P是棱C1D1上的动点,则四面 体PQEF的 体 积( )。

图3
A.有最小值的一个变量
B.有最大值的一个变量
C.没有最值的一个变量
D.一个不变量
错解:选A 或B或C。
错因剖析:忽略三棱锥体积等积变换的目标:找出易求的底面和高。
正解:连接QA,则QA为Q点到AB的距离。又因为EF=2,故S△QEF为定值。又因为C1D1∥AB,则由线面平行的判定定理易得C1D1∥面QEF。又P是棱C1D1上的动点,故P点到平面QEF的距离也为定值,即四面体PQEF的底面积和高均为定值,所以四面体PQEF的体积为定值。故选D。
提醒:对于三棱锥的体积,可任选一面作底面,目标是易求出该底面面积和对应的高。
易错3——将空间问题转化为平面问题时,缺少割补法的意识
例3一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞D,E,F,且知SD∶DA=SE∶EB=CF∶FS=2∶1,如图4 所示,若仍用这个容器盛水,则最多可盛水的体积是原来的( )。
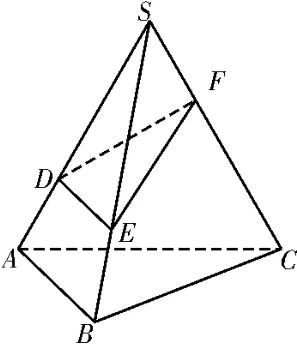
图4
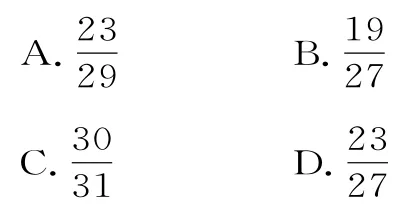
错解:选A 或B或C。
错因剖析:不理解这个容器盛水最多的意义,由过D或F作面ABC的平行平面,通过规则几何体的体积求出不规则几何体的体积。
正解:当平面EFD处于水平位置时,容器盛水最多,所以则最多可盛水的体积是原来故选D。
提醒:理解这个容器盛水最多的意义是解答的关键,将非规则体转化为规则体进行求解。
易错4——缺少 “作直接面化斜为直”割补法求体积的意识
例4斜三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长等于b,一条侧棱AA1与底面相邻两边AB、AC都成45°角,求这个三棱柱的侧面积和体积。
错解:侧面积体积
错因剖析:错解中把三棱柱当作直三棱柱求侧面积和体积,缺少作直截面化斜为直的方法。
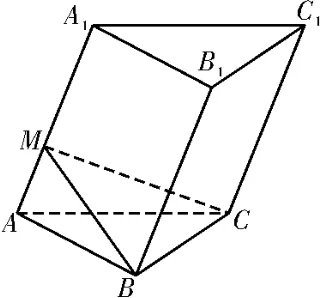
图5
正解:“过BC作平面与AA1垂直于M”是求解的关键。 如图5,过点B作BM⊥AA1于M,连接CM,在△ABM和△ACM中, 因 为AB=AC,∠MAB= ∠MAC=45°,MA为公共边,所以△ABM≌△ACM,所以∠AMC= ∠AMB=90°,所 以AA1⊥ 面BMC,即平面BMC为直截面。又BM=CM所以△BMC的周长为因为棱长为b,所以S侧= (1+ 2)ab,V=S△BMC·AA1=
提醒:斜棱柱的侧面积和体积的计算,常常依据题设的特殊性构建棱的直接面,利用割补法化归为底面为直接面、高为侧棱长的直棱柱,其S侧=C直截面×L侧棱,V=S直截面×L侧棱。
易错5——盲目类比平面几何中的定理和性质
例5如图6 所示,已知E,F分别是正方体ABCD-A1B1C1D1的棱AA1,CC1上的点,且AE=C1F。 求 证:四 边 形BED1F是平行四边形。
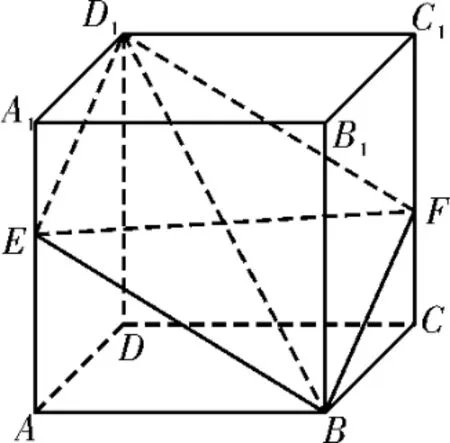
图6
错 解:在 正 方 体ABCD-A1B1C1D1中,平面A1ADD1∥平面B1BCC1,由两平行平面与第三平面相交得交线平行,故D1E∥FB,同理可证D1F∥EB,故四边形EBFD1为平行四边形。
错因剖析:盲目地套用平面几何定理。
正解:在△ABE和△C1D1F中,因为AB=C1D1,AE=C1F,∠EAB= ∠FC1D1=90°,所以Rt△EAB≌Rt△FC1D1,所以EB=D1F。 同 理 可 证D1E=BF。 连 接EF,BD1,则它们相交于各自中点,从而B,E,F,D1四点在同一平面内。 所以四边形EBFD1是平行四边形。
提醒:平面几何中的有关结论在空间不一定成立,平面几何中的结论在立体几何中应用时应遵循两点:(1)空间中放在同一平面内用;(2)先证明在空间是真命题再用。
易错6——折叠问题中忽视折叠前后的“不变量”
例6△ABC的边BC上的高线为AD,BD=a,CD=b,将△ABC沿AD折成大小为θ的二面角B-AD-C,若则三棱锥A-BCD的侧面三角形ABC是( )。
A.锐角三角形
B.钝角三角形
C.直角三角形
D.形状与a、b的值有关的三角形
错解:选D。
错因剖析:将平面图形折成空间图形后线面位置关系理不清,易瞎猜。
正解:作出平面图形(图7)和空间图形(图8),寻求折叠前后在同一平面内的图形为不变量切入,如图8,且BD=a,CD=b,由余弦定理所以BC2=b2-a2,则BD⊥BC。又AD⊥面BCD,所以AD⊥BC,所 以BC⊥ 面ABD,所以BC⊥AB,即△ABC为直角三角形。故选C。
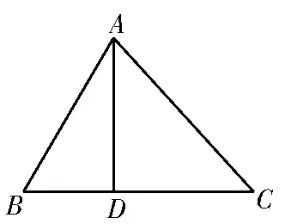
图7
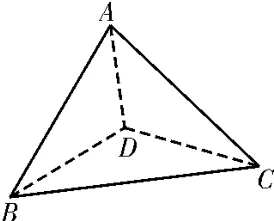
图8
提醒:翻折与展开是一个问题的两个方面,均要注意平面图形与立体图形各个对应元素的相对变化,元素间的大小与位置关系。在翻折过程中,处在同一个半平面内的元素是不变的,弄清这一点是解决这类问题的关键。
易错7——混淆二面角与两向量夹角的概念
例7如图9,在四棱锥V-ABCD中, 底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD,求 二面角A-VD-B的余弦值。
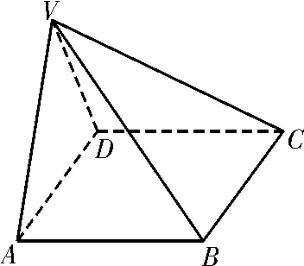
图9
错解:过V作VO⊥AD于O,由已知平面VAD⊥底面ABCD,所以VO⊥底面ABCD,所以以OA,OV分别为x轴,z轴建立如图10所示的空间坐标系,分别计算出面VAD与面VBD的法向量为n1=(0,1,0),所 以
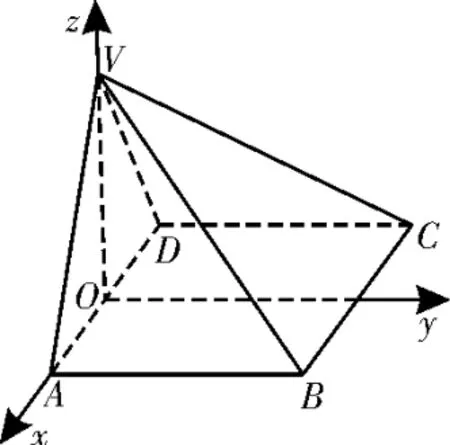
所以二面角A-VD-B的余弦值为
剖析:法向量的夹角与二面角相等或互补,本题中观察知二面角A-VD-B为锐二面角。
正解:错解中应补充,由图形知二面角A-VD-B为锐二面角,则二面角A-VD-B的余弦值为
提醒:利用空间向量求二面角,先求两平面的法向量,利用向量的夹角公式求出两法向量的夹角,二面角的平面角与法向量的夹角相等或互补,具体是哪一种,一般有两种判断方法:(1)根据图形判断二面角是锐角还是钝角;(2)根据两法向量的方向判断。
