高慧明老师讲数学(2)
——以圆锥曲线的几何性质为背景的压轴选择题
2019-12-06北京市第十二中学高慧明
■北京市第十二中学 高慧明
高考数学试题中以圆锥曲线的几何性质为背景的压轴选择题主要涉及以下几种类型问题:求圆锥曲线的离心率,求特定字母的取值范围,求圆锥曲线中的最值,以及平面图形与圆锥曲线相结合的问题。
类型一、求圆锥曲线的离心率问题
例1如图1,已知双曲线b>0)的左、右焦点分别为F1、F2,A是双曲线的左顶点,双曲线C的一条渐近线与直线交于点且F1P⊥AM,则双曲线C的离心率为( )。
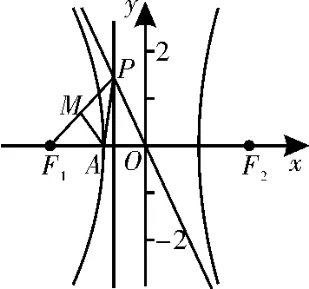
图1
解析:已知双曲线b>0)的左顶点为A(-a,0),左焦点为F1(-c,0),由知M为线段F1P的中点,且F1P⊥AM,可得|AP|=|AF1|,由题意知渐近线OP的方程为则有所以由|AP|=|AF1|得即a2(c-a)2+a2b2=c2(c-a)2,即(c2-a2)(c-a)2=a2b2,可得c-a=a,即c=2a,所以故选C。
评注:在求解有关离心率的问题时,一般并不是直接求出c和a的值,而是根据题目给出的椭圆或双曲线的几何特征,建立关于参数c,a,b的方程或不等式,通过解方程或不等式求得离心率的值或范围。一般来说,求离心率的取值范围,通常可以从两个方面来研究:一是考虑几何关系,例如根据线段的大小关系或者角的大小关系列不等式;二是考虑代数关系,通过设点,将所给问题坐标化,结合圆锥曲线方程和本身的范围来确定。

相关链接1.已知椭圆b>0)的左、右焦点分别为F1、F2,过F1且与x轴垂直的直线交椭圆于A,B两点,直线AF2与椭圆的另一个交点为C,若S△ABC=3S△BCF2,则椭圆的离心率为( )。

解析:设椭圆的左、右焦点分别为F1(-c,0)、F2(c,0),由x=-c,代入椭圆方程可得可设y),由S△ABC=3S△BCF2。 可 得即有即2c=2x-可得代入椭圆方程可得由c2,可得,解得故选A。
类型二、与圆锥曲线有关的最值问题和取值范围问题
例2在等腰梯形ABCD中,AB∥CD,且|AB|=2,|AD|=1,|CD|=2x,其中x∈(0,1),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,若对任意x∈(0,1)都有不等式恒成立,则t的最大值为( )。

解析:如图2,过D作DE⊥AB交AB于E,则AE=1-x,EB=1+x,所以所以e1=所以则e1+e2因为所以e1+e2>所以故选C。
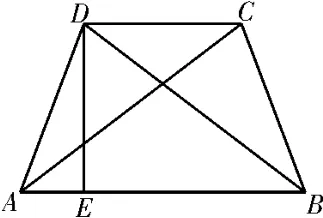
图2
评注:抛物线的定义是转化抛物线上的点到焦点距离和到准线距离的桥梁,通过设点的坐标并结合抛物线的定义,将待求对象坐标化,同时结合抛物线的方程消元,利用函数思想求解最值问题是常见的求最值的方法,有时还可以用几何平面几何知识求解。
相关链接2.如图3,直线x=m与抛物线x2=4y交于点A,与圆x2+(y-1)2=4 的实线部分(即在抛物线内的圆弧)交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )。
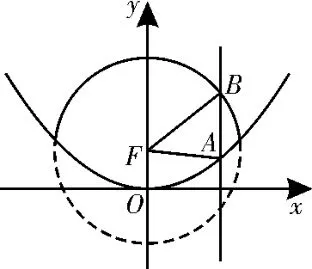
图3
A.(4,6) B.(4,6]
C.(2,4) D.(2,4]
解析:因为圆x2+(y-1)2=4的圆心为(0,1),抛物线的方程为x2=4y,所以圆心与抛物线的焦点重合,所以|FB|=2,|AF|=yA+1,|AB|=yB-yA,所以△ABF的周长为2+yA+1+yB-yA=yB+3。因为1<yB<3,所以△ABF的周长的取值范围是(4,6)。故选A。
相关链接3.已知直线x+y-k=0(k>0)与圆x2+y2=4交于不同的两点A,B,O是坐标原点,且有那么k的取值范围是( )。

解析:设AB的中点为D,则OD⊥AB。因为所 以所 以因 为所以因为直线x+y-k=0(k>0)与圆x2+y2=4交于不同的两点,所以所以1≤即解得故选C。
类型三、平面图形与圆锥曲线相结合的问题
例3设双曲线>0)的左焦点为F(-c,0),点M,N在双曲线C上,O是坐标原点,若四边形OFMN为平行四边形,且四边形OFMN的面积为cb,则双曲线C的离心率为( )。

解析:设M(x0,y0),因为四边形OFMN为平行四边形,所以因为四边形OFMN的面积为所以即所以代入双曲线方程得因为e>1,所以故选D。
评注:求离心率问题实质上是根据已知条件,挖掘题中a,b,c的等量关系或者不等关系,可以借助平面图形自身满足的条件或者点的坐标所满足的方程或者范围等,本题利用平行四边形的性质并结合双曲线方程和平行四边形的面积公式得到关于a,b,c的方程,进而确定离心率的值。
相关链接4.已知椭圆和双曲线有共同的焦点F1,F2,P是它们的一个交点,且记椭圆和双曲线的离心率分别为e1,e2,则的最大值为( )。
解析:考查一般性结论,当∠F1PF2=θ时,设|PF1|=m,|PF2|=n,椭圆的长半轴长为a1,双曲线的长半轴长为a2,两曲线的焦距为c,结合题意有m+n=2a1,|m-n|=2a2。两式平方相加可得m2+n2=2(+);两式平方作差可得mn=-。由余弦定理得4c2=m2+n2-2mncosθ,则4c2=即2c2=(1-即结合二倍角公式有
【归纳领悟】
1.求解圆锥曲线的离心率的常用方法
求椭圆、双曲线的离心率,关键是根据已知条件确定a,b,c的等量关系,然后把b用a,c代换,最后求得的值。在双曲线中,由于故双曲线的渐近线与离心率密切相关。求离心率的范围问题关键是确立一个关于a,b,c的不等式,再根据a,b,c的关系消掉b得到关于a,c的不等式,由这个不等式可以确定a,c的关系,从而求得离心率的范围。
2.求解特定字母取值范围问题的常用方法
(1)构造不等式法。根据题设条件及曲线的几何性质(如:曲线的范围、对称性、位置关系等),建立关于特定字母的不等式或不等式组,然后解不等式或不等式组,从而求得特定字母的取值范围。
(2)构造函数法。根据题设条件,用其他的变量或参数表示欲求范围的特定字母,即建立关于特定字母的目标函数,然后研究该函数的值域或最值情况,从而得到特定字母的取值范围。
(3)数形结合法。研究特定字母所对应的几何意义,然后根据相关曲线的定义、几何性质,结合数形结合的方法求解。
3.求解圆锥曲线中的最值问题的常用方法
(1)几何方法。利用曲线的定义、几何性质,以及平面几何中的定理、性质等进行求解。
(2)代数方法。把要求最值的几何量或代数表达式表示为某个(些)参数的函数(解析式),然后利用函数方法、不等式方法等进行求解。
常见的几何方法有:①直线外一定点P到直线上各点距离的最小值为点P到直线的垂线段的长度;②圆C外一定点P到圆上各点距离的最大值为|PC|+r,最小值为|PC|-r(r为圆C半径);③过圆C内一定点P的圆的最长的弦即为经过P点的直径,最短的弦为过P点且与经过P点的直径垂直的弦;④圆锥曲线上本身存在最值问题,如:椭圆上两点间最大距离为2a(长轴长);双曲线上两点间最小距离为2a(实轴长);椭圆上的点到焦点的距离的取值范围为[a-c,a+c],a-c与a+c分别表示椭圆的焦点到椭圆上点的最小与最大距离;抛物线上的点中顶点与抛物线的准线距离最近。
常用的代数方法有:①利用二次函数求最值;②通过三角换元,利用正、余弦函数的有界性求最值;③利用基本不等式求最值;④利用导数法求最值;⑤利用函数单调性求最值。
