2019 年高考“立体几何经典问题”聚焦

■江苏省口岸中学 曹 艳

2019 年高考对立体几何的考查始终围绕 “空间问题平面化、模型化和代数化”展开的。本文以2019年的高考真题为载体,探究立体几何经典问题求解的思维方法,希望对同学们的学习或复习有所启示。

聚焦1——几何体的体积或表面积的计算

例1(2019 年高考江苏卷9)如图1,长方体ABCD-A1B1C1D1的体积是120,E为CC1的中点,则三棱锥E-BCD的体积是_____。

图1

解析:由题意结合几何体的特征和所给几何体的性质可求得三棱锥的体积。因为长方体ABCD-A1B1C1D1的体积为120,所以AB·BC·CC1=120。因为E为CC1的中点,所以

由长方体的性质知CC1⊥底面ABCD,所以CE是三棱锥E-BCD的底面BCD上的高,所以三棱锥E-BCD的体积

回味:求解组合体的体积或面积,关键是准确理解几何体的定义,真正把握几何体的结构特征,借助正方体和长方体等几何模型,在几何模型中确定底面和高,用体积或面积公式计算。本题蕴含 “整体和局部”的对立统一规律。在几何体的表面积或体积的计算问题中,往往需要理清整体和局部的关系,灵活利用 “割”与 “补”的方法解题。

聚焦2——多面体外接球中的“补形法”

例2(2019年高考全国Ⅰ卷理12)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2 的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,如图2所示,则球O的体积为( )。

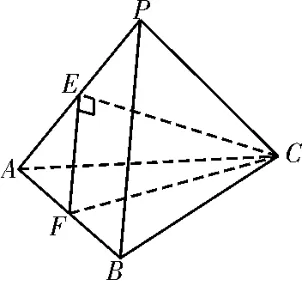
图2

解析:正三棱锥的外接球,把握其特殊性,先证得PB⊥平面PAC,再求得PA=PB=PC=从而得三棱锥P-ABC为正方体一角,补形后知体对角线即为球的直径。

因为PA=PB=PC,△ABC是边长为2的正三角形,所以三棱锥P-ABC为正三棱锥,所以PB⊥AC。

又E,F分别为PA,AB的中点,所以EF∥PB,所以EF⊥AC。

又EF⊥CE,CE∩AC=C,所以EF⊥平面PAC。

又EF∥PB,所以PB⊥平面PAC,所以PB⊥PA,PB⊥PC,所以PA=PB=PC

所以三棱锥P-ABC为正方体的一部分即所以球O的体积故选D。

回味:正三棱锥的对边互相垂直和题设的垂直条件得到正三棱锥从顶点出发的三条侧棱两两垂直,从而得到该正三棱锥是正方体的一角,将特殊的正三棱锥补成正方体即可解决外接球问题。

聚焦3——等积法求解“点到平面的距离”

例3(2019 年高考全国Ⅰ卷文19)如图3,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点。

图3

(1)证 明:MN∥平 面C1DE;

(2)求点C到平面C1DE的距离。

解析:(1)构造平行四边形找到线和面内的直线平行。如图4,连接ME,B1C,因为M,E分别为BB1,BC的中点,所以ME为△B1BC的中位线,所以ME∥B1C且

又N为A1D的中点,且A1D■B1C,所以ND∥B1C且

所以ME■ND,所以四边形MNDE为平行四边形,所以MN∥DE。

又MN⊄平面C1DE,DE⊂平面C1DE,所以MN∥平面C1DE。

(2)构造三棱锥利用等积法求点到面的距离。在菱形ABCD中,E为BC的中点,所以DE⊥BC,根据题意有因为棱柱为直棱柱,由面面垂直的性质定理有DE⊥平面BCC1B1,所以S△DEC1=

设点C到平面C1DE的距离为d,根据题意有V三棱锥C1-CDE=V三棱锥C-C1DE,则有解得d=所以点C到平面C1DE的距离为

回味:等积法求解点到平面的距离,不需要直接找到点到平面的垂线段,利用一个几何体的不同面作底面时几何体的体积不变列出等式,间接求出点到平面的距离。常常构造三棱锥换底可求点到平面的距离。

聚焦4——几何法求解线面角

例4(2019 年高考天津卷文17)如图5,在四棱锥P-ABCD中,底面ABCD为平行四边形,△PCD为等边三角形,平 面PAC⊥平面PCD,PA⊥CD,CD=2,AD=3。

图5

(1)设G,H分别为PB,AC的中点,求证:GH∥平面PAD;

(2)求证:PA⊥平面PCD;

(3)求直线AD与平面PAC所成角的正弦值。

解析:(1)结合平行四边形的性质,以及三角形中位线的性质进行证明。

如图6,连接BD,易知AC∩BD=H,BH=DH。

图6

因为BG=PG,所以GH∥PD。

又因为GH⊄平面PAD,PD⊂平面PAD,所以GH∥平面PAD。

(2)如图6,取棱PC的中点N,连接DN,依题意得DN⊥PC,结合面面垂直的性质及线面垂直的性质得到DN⊥PA,利用线面垂直的判定定理进行证明。

因为△PCD为等边三角形,依题意得DN⊥PC。

又因为平面PAC⊥平面PCD,平面PAC∩平面PCD=PC,所以DN⊥平面PAC。

又PA⊂平面PAC,故DN⊥PA。

又因为PA⊥CD,CD∩DN=D,所以PA⊥平面PCD。

(3)利用线面角的平面角的定义找角。连接AN,由(2)知DN⊥平面PAC,所以∠DAN为直线AD与平面PAC所成的角。

因为△PCD为等边三角形,CD=2,且N为PC的中点,所以

又DN⊥AN,在 Rt △AND中,所以直线AD与平面PAC所成角的正弦值为

回味:求直线和平面所成角,关键在于找到斜线在平面上的射影,找射影的关键在于找到平面的垂线段,得到垂足,连接斜足和垂足就是射影。常常用到线线垂直、线面垂直和面面垂直的相互转化。

聚焦5——向量法探究 “线面角和二面角” 的大小

例5(2019 年高考天津卷理17)如图7,AE⊥平面ABCD,CF∥AE,AD∥BC,AD⊥AB,AB=AD=1,AE=BC=2。

图7

(1)求 证:BF∥ 平 面ADE;

(2)求直线CE与平面BDE所成角的正弦值;

(3)若二面角E-BD-F的余弦值为求线段CF的长。

解析:利用几何体的特征建立空间直角坐标系,用向量法求解。依题意,可以建立以A为 原 点,分 别 以的正方向为x轴,y轴,z轴正方向的空间直角坐标系,如图8所示。由AE⊥平面ABCD,CF∥AE,AD∥BC,AD⊥AB,AB=AD=1,AE=BC=2,可得A(0,0,0),B(1,0,0),C(1,2,0),D(0,1,0),E(0,0,2)。

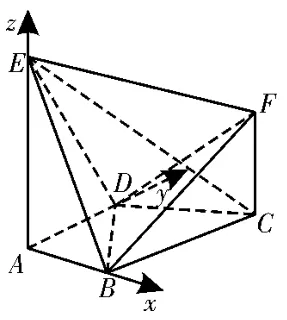
图8

设CF=h(h＞0),则F(1,2,h)。

(1)探究直线BF的方向向量和平面ADE的法向量的关系。

又因为直线BF⊄平面ADE,所以BF∥平面ADE。

(2)利用直线CE的方向向量和平面BDE的法向量求解线面角的正弦值。

不妨令z=1,可得n=(2,2,1),因此有

所以直线CE与平面BDE所成角的正弦值为

(3)确定两个半平面的法向量,然后利用二面角的余弦值计算公式得到关于CF长度的方程,解方程可得CF的长度。

设m=(x,y,z)为平面BDF的法向量,则即

不妨令y=1,可得

经检验,符合题意。

所以线段CF的长为

回味:利用法向量可探究线面的位置关系,可求解空间的角,关键在于:第一,破 “建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破 “求法向量关”,构建方程组求出平面的法向量;第四,破 “应用公式关”,准确理解和熟练应用夹角公式|cosθ|=|cos〈m,n〉|=求解空间角。