高含水油藏薄砂体精细刻画技术探讨

张会卿，周宗良，曹国明，燕 云

(中国石油大港油田公司勘探开发研究院 天津300280)

0 引 言

大港 X开发区位于北大港构造带东部，构造异常破碎，主力层明化镇组受曲流河河道迁移摆动影响，储层具有单砂体厚度薄、横向变化快等特点，均属于 1/4地震波波长以下的薄砂体[1]，无法从地震剖面上直接识别。为了解决上述问题，将“两宽一高”地震勘探理念引入该区复杂油藏薄砂体精细预测中。本次依托高密度地震资料，创新提出基于小入射角道集叠加的最大熵地震频谱分解预测方法，综合利用小入射角道集叠加处理、薄层调谐分析、井震多参数交会等方法，破解了复杂地表条件下地震采集频率低的业界难题，建立了调谐频率、调谐厚度和砂岩厚度的关系，实现了单一薄砂体的准确预测。

1 小入射角叠加处理

1.1 技术原理

俞寿朋[2]指出，地震勘探分辨率随炮检距增大而降低。由于地下介质是一组或多组由不同断层、裂缝等组成的地层，地震波在传播过程中要发生不同程度的衰减。总体而言，同一深度下，入射角越小，炮检距越小，地震波能量和频率的衰减程度越低。

下面论证地震波入射角与分辨率之间的理论关系[3]。假设存在一水平地层，地层顶面、底面埋深分别为H1、H2，地层厚度为h，地层顶、底面地震波入射角分别为θ1、θ2，地层上覆介质速度为 V1，地层速度为 V2。由于 H2、H1h，则有：

地层顶界面双程旅行时 t1和底界面双程旅行时t2可分别表达为：

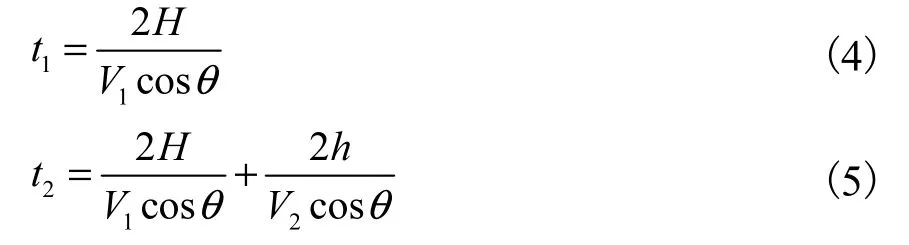
由于 V1≈V2=V，则地层顶底界面双程旅行时平方差为：

因为H≫h，所以上式可整理为：

根据Rayleigh准则，双程旅行时差为1/2周期时达到地震纵向分辨率极限，则有：

此时可分辨地层厚度近似为：

根据公式 9可得，对于某一时间深度(t0)处的地层，入射角越小，则可分辨储层厚度越小，即分辨率越高。因此，选取小入射角道集进行叠加处理，可提高地震分辨率。

常规地震资料由于覆盖次数不足，难以确保小入射角道集的有效叠加处理，而高密度地震资料则由于地震采样点密集、覆盖次数高的特点，破解了这一难题。

1.2 应用实例

本次应用“两宽一高”地震数据体覆盖次数为360次。其中，0～10°入射角覆盖次数为 32～37次，0～20°入射角覆盖次数为 140次，大于 25°的大角度入射角覆盖次数为 78～86次。本次以确保入射角较小和覆盖次数较高为原则，选取 0～20°入射角道集进行叠加处理。

图1为全叠加剖面与小入射角道集叠加剖面对比实例。图1c显示，lq5-9、lq7-8等井 NmⅢ-4发育2层薄砂体NmⅢ-4-1、NmⅢ-4-2，这2层砂体从全叠加剖面(图1a)难以识别，但在小入射角道集叠加剖面中(图1b)却能够非常清晰地识别出来，表明通过选取小入射角道集进行叠加处理，可以提高地震垂向分辨能力。

图1 NmⅢ-4小层地震剖面对比Fig.1 Comparison of NmⅢ-4 formation seismic sections

2 最大熵谱分解

2.1 技术原理

20世纪90年代中期，Partyka等[4]首次提出谱分解概念，即利用时频分析方法，通过数学变换将地震信息从时间域转换到频率域，进而精确表征地震信号中每一时间点的频率成分[5]，继而衍生出离散傅里叶变换、最大熵等多种谱分解算法。

最大熵在 1967年由 J.P.伯格提出，用来衡量信息的不确定性；之后 Aydm Akan[6]等将最大熵引入地震信号分析，用于计算地震信号的功率谱。最大熵谱分解原理如下：地震记录x(t)为一个平稳的离散时间序列，其熵的表达式为[7]：

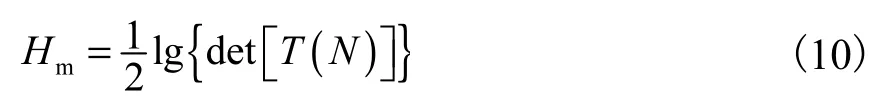
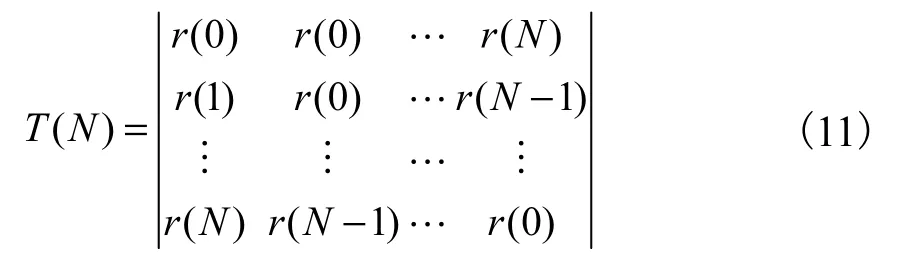
式中：Hm为熵，J/mol·K；t＝1，2，...，N+1，ms；T(N)为托布里兹形式的信号矩阵，dB。若 r(0)，r(1)，...，r(N)值已知，则可重复利用递推算法求取 r(N+1)，r(N+2)，...的值。

地震数据道x(t)可用一个 K阶自回归差分方程模拟：

相应的地震信号功率谱P(f)为：

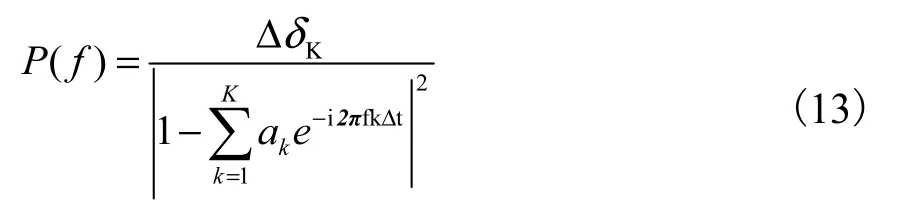
式中：x(t)为地震数据道，CDP's/cm；e(t)为预测误差，CDP's/cm；ΔδΚ为预测误差的方差；P(f)为地震信号功率谱，dB2/Hz；ak为预测误差滤波器的系数，无量纲；k 为常数，k＝1，2，...，K；f 为角频率，rad/s；Δt 为采样间隔，ms。

最大熵谱分解确保地震记录在分析时窗内的自相关函数符合已知数据要求，而使时窗外自相关函数的不确定性最大。相比傅里叶变换要求地震信号在(-∞，+∞)之间取值，最大熵减少了因时窗长度有限而产生的误差。最大熵谱分解可生成调谐体。

调谐体预测薄砂体厚度源于 Widess模型：Widess楔形模型证实，1/4波长以下薄层的顶、底反射界面发生干涉[1]；Kallweit得出薄层等于 1/4波长时将产生调谐效应，且调谐点处振幅值最大[8-9]。黄绪德[10]论证了薄层振幅谱的周期性陷频特征，其陷频周期和频率互为倒数。边立恩等[11]论证了薄层调谐频率与调谐厚度关系，推导出调谐厚度估算公式：

式中：ΔZ为调谐厚度，m；v为目的层速度，m/s；f0为调谐频率，Hz。

2.2 应用实例

利用最大熵法制作调谐体并得到调谐频率，调谐体时窗依据砂岩时间厚度确定为 30ms。东西向调谐体剖面中，A1井调谐频率约为 25Hz，向两翼调谐频率急剧升高，反映调谐厚度减薄(图2)；南北向调谐体剖面中，调谐频率始终稳定在 25～30Hz，反映调谐厚度基本不变(图3)。调谐体剖面反映岩性边界更加直观，且与单频体切片对应性很好。

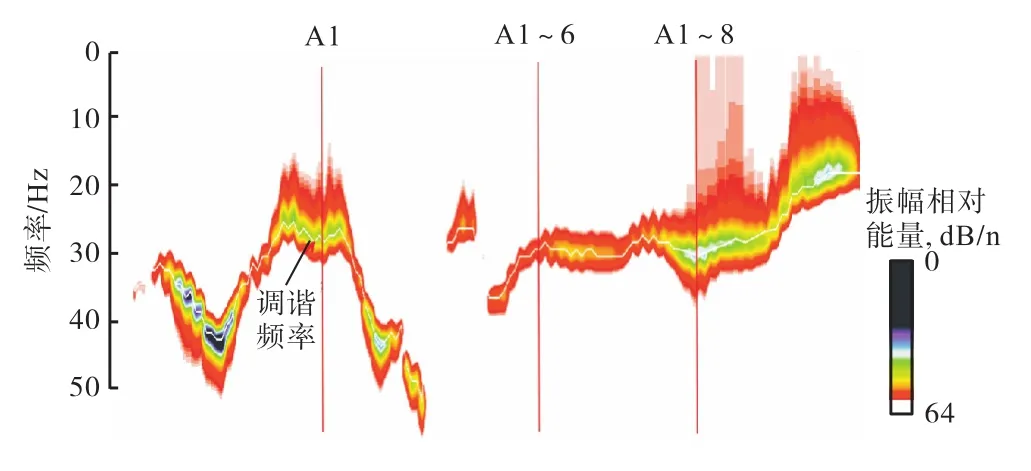
图2 A1井-A1-8井最大熵调谐体剖面Fig.2 Maximum entropy tuning cube profile of wells A1-A1-8

图3 A1-3井-A1-7井最大熵调谐体剖面Fig.3 Maximum entropy tuning cube profile of wells A1-3-A1-7

马跃华等[12]利用调谐频率计算调谐厚度，单砂体厚度误差为15%～83%。误差源于以下因素[13]：①任何算法均存在误差，造成调谐频率的求取不准确；②由于单砂体厚度的空变性，难以用一个确定的调谐体时窗确保只有目的层地震信号参与计算；③地震信号中低频噪声与有效的低频信息相夹杂，影响低频端厚度估算；④受测不准原理、测井-地震观测频率不同、储层物性参数不同等因素的影响[14-15]，速度参数难以准确获取。因此，调谐厚度不能直接表征单砂体厚度，而应理解为相对厚度。在地层速度较稳定的地区，可通过统计完钻井资料，建立调谐厚度与单砂体厚度相对关系，从而求取井间单砂体厚度。

本次统计了 15口完钻井的储层参数，利用声波时差获取单井层速度，代入调谐厚度估算公式，计算得到调谐厚度。通过建立多井调谐厚度和单砂体厚度关系，证实二者呈线性正相关(图4)，关系式为：

式中：Z为单砂体厚度，m；ΔZ为调谐厚度，m。

3 应用效果

应用公式(15)完成单砂体厚度预测(图5)，在此基础上优选构造有利区部署2口新井A1-1-1和A1-1-2，新井成功钻遇 NmⅢ-8-2储层，且单砂体厚度与预测厚度吻合率达 90%以上。钻井结果与预测结果吻合，证明基于最大熵谱分解方法的单砂体定量预测方法在本区适用。

图4 A1井区单砂体厚度与调谐厚度关系Fig.4 Relation between thickness of single sand body and tuning thickness in well A1 area

图5 A1井区NmⅢ-8-2砂岩厚度等值图Fig.5 Contour map of NmⅢ-8-2 sandstone thickness in well A1 area

4 结 论

①地震纵向分辨率与地震波入射角近似呈正比，基于“两宽一高”的小入射角道集叠加处理能够有效提高地震资料垂向分辨能力。

②应用最大熵谱分解可得到薄层调谐体，利用调谐频率可计算调谐厚度。

③单一薄砂体厚度和调谐厚度呈线性正相关关系，据此可实现井间单一薄砂体厚度预测。