直角坐标系下三维轴对称非齐次不可压缩MHD方程的基本能量估计

刘芳君，马 倩

(云南民族大学 数学与计算机科学学院，云南 昆明 650500)

0 引言

磁流体(Magnetohydrodynamics,MHD)是涉及磁场和导电流体之间相互作用的研究，例如：等离子体、液态金属、盐水和电解质等，MHD方程是研究磁特性和导电流体动力学行为的一个方程.MHD方程最早由Hannes Alfvén[1]提出，他也因此获得了1970年的诺贝尔物理学.

由于MHD方程是Navier-Stokes方程和Maxwell方程耦合得到的，目前，关于MHD方程的数学理论研究还很少.Duraut和Lions[2]构造了一类能量有限弱解和一类局部强解，特别地，二维的局部强解已经被证明是整体的而且是唯一的，更多的研究见文献[3-6]等；侯一钊和李从明[7]证明了具有涡旋的三维轴对称Navier-Stokes方程的动态稳定性；之后，王术和吴继晖[8]用侯一钊的方法构建了一系列电阻MHD方程(uθ=Br=Bz=0)的整体光滑解；雷震[9]在流体速度和磁场中分量为零的条件下，即(uθ=Bθ=0)，证明了轴对称MHD方程的全局适定性；2017年，苏文火、郭真华和杨干山[10]在不要求流体速度和磁场中的分量为零的条件下，证明了三维柱对称的一类大初值的整体光滑解的存在性.

本文主要针对三维轴对称非齐次不可压缩MHD方程的基本能量估计展开研究，即文献[10]中的引理4.1，该引理对后续证明MHD方程解的存在性至关重要.文献[10]考虑的是柱对称条件下的MHD方程的基本能量估计，在柱坐标系下将原始的MHD方程中的第2个和第3个等式转变成了文献[10]中式(2.6)和(2.7)中的6个等式，且将质量守恒和不可压缩约束条件转变成了式(2.5)和(2.8)的形式，在一定程度上限制了MHD基本能量估计的应用范围，简化了其求解过程.为了使MHD方程基本能量估计的适用范围较广，本文将推导三维轴对称非齐次不可压缩MHD方程在直角坐标系下的基本能量估计.

1 三维轴对称非齐次不可压缩MHD方程在直角坐标系下的模型

三维轴对称非齐次不可压缩MHD方程为

(1)

将质量守恒方程和不可压缩条件分别转换为直角坐标系下的形式，即

ρt+div(ρu)=0⟹ρt+ρx1u1+ρx2u2+ρx3u3=0,

(2)

(3)

其中，x1、x2和x3分别表示直角坐标系的3个坐标轴，u1、u2和u3分别表示每个坐标轴对应的u的分量，B1、B2和B3分别表示每个坐标轴对应的B的分量，u1x1表示u1对x1求偏导，u2x2、u3x3、B1x1、B2x2、B3x3的含义与u1x1类似.

将式(1)中的第2个等式乘以u，第3个等式乘以B，并将其在直角坐标系下的展开得

(4)

(5)

其中，ux1x1表示u对x1求2次偏导，ux2x2、ux3x3、Bx1x1、Bx2x2、Bx3x3的含义与ux1x1类似.

将式(4)和式(5)相加并积分，整理后可得

(6)

将式(6)进一步化简、整理可得

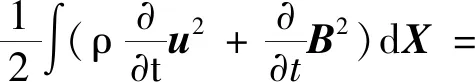
(7)

下面将在下一节对式(7)进行详细推导.

2 MHD方程的基本能量估计

本节主要完成式(7)的推导.下面，将利用式(2)和(3)的约束条件对式(7)中等式右端包含的6项进行详细推导，即分别对Ia至If进行推导.先来看第一项Ia，即

(8)

将式(8)拆成2部分，即Ia1和Ia2，其可分别表示为

通过仿真验证,在添加了卡尔曼滤波程序后,极大地改善了锁相环的输出,且扩展了锁相环可跟踪的信噪比范围。通过仿真验证,本文的算法最大可提取信噪比在-20 dB左右的信号。

(9)

(10)

下面，分别对Ia2中的每一项进行单独计算，即

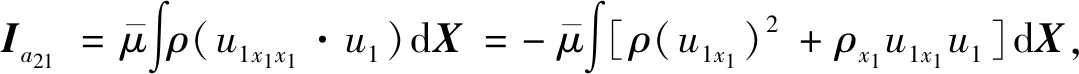
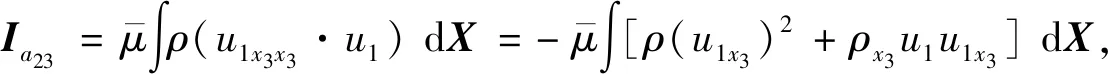
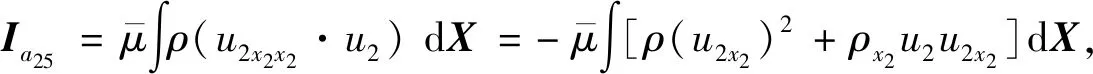
结合式(9)和Ia21至Ia29可知，Ia1中的全部项均可在Ia2中找到相应项的相反值，故可全部抵消.最终得到的Ia为

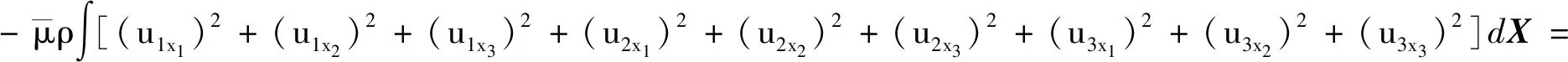
(11)

第2项Ib可以表示为

(12)

通过对比式(12)和(10)可知，两者在形式上基本相同，只是式(12)中的系数υ是常量，因此，采用与Ia2相同的推导方式，最终得到的Ib为

(13)

第3项Ic可以表示为

(14)

采用与Ia2相同的推导思路，分别对Ic中的每一项进行单独计算，即

(15)

结合式(15)和Ic1至Ic9，Ic可进一步化简为

(16)

利用式(2)所表示的质量守恒方程，最终得到的Ic为

(17)

(18)

第5项Ie可以表示为

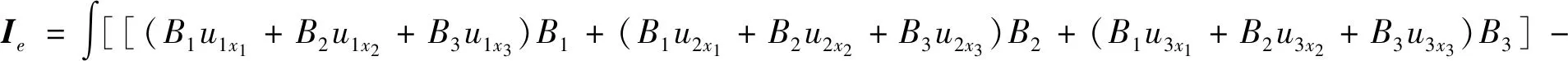
(19)

采用与Ia2相同的推导思路，分别对Ie中的每一项进行单独计算，即

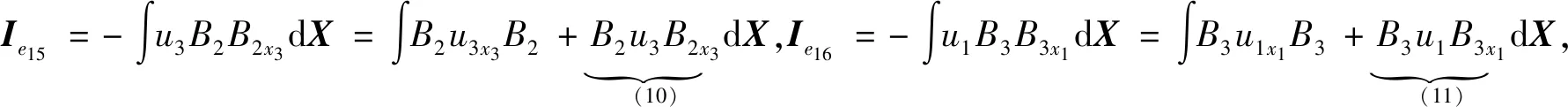
(20)

Ie10+Ie11+Ie12=0，Ie13+Ie14+Ie15=0，Ie16+Ie17+Ie18=0.

(21)

结合式(18)、(20)和(21)，可得

Id+Ie=0.

(22)

第6项If可以表示为

(23)

至此，式(7)右侧包含的6项已全部求解完毕.利用式(11)、(13)、(17)、(22)和(23)，将右侧6项相加后可得

(24)

结合式(7)和(24)，并对式(7)两端同时对t在[0,T]的范围内进行积分，最终推导得到三维轴对称不可压缩MHD方程在直角坐标系下的基本能量估计为

(25)

3 结语

本文主要研究三维轴对称非齐次不可压缩MHD方程在直角坐标系下的基本能量估计，通过在原始MHD方程的第2个式子和第3个式子的两端分别乘以u和B，将相乘后的第2个式子和第3个式子相加并在直角坐标系下展开，利用直角坐标系下的质量守恒公式和不可压缩条件，最终推导得到了MHD方程在直角坐标系下的基本能量估计，为后续MHD方程在直角坐标系下解的存在性证明奠定了基础.