基于split-and-conquer和非参数向前选择法的变量选择

李顺勇，赵永胜

(山西大学 数学科学学院，山西 太原 030006)

大数据时代，为获取更多的数据提供了便利条件，也给数据研究带来了挑战.当数据维数远远高于样本量时，很多常用的经典算法往往举步维艰.面对巨多杂乱的数据，如何处理，才能为研究做数据支撑？统计学者把变量选择作为解决这一问题的突破口.选择出相关性高的变量，为进一步对模型进行预测和解释埋下伏笔.Fan和Lv[1]将变量选择作为处理超高维数据的突破口.目前最常用的变量选择方法有：基于统计学方法的主成分分析、充分降维、偏最小二乘回归、全部子集法等.其中，李正欣等[2]提出了一种基于共同主成分的降维方法；解洪胜等[3]介绍3种非线性降维算法的概念和实现步骤；李向杰等[4]提出了一种稳健的降维方法，使用了切片逆回归方法.基于范数的变量选择方法有：岭回归、Lasso回归、弹性网回归及SCAD等.其中，Tibshirani[5]提出的Lasso方法已经得到了广泛的运用；Efron 等[6]提出了LARS算法；Sherwood[7]利用 SCAD估计方法和MCP估计算法进行变量选择；Zhang[8]在进行降维的过程中，既保留了数据的代表性又节省了运算空间.

上述方法适用于线性回归的变量选择，而对于复杂的模型，尤其当数据维数比较大的时候，会出现消耗时间过长的问题.并且当数据的维数大于样本量时，变量选择的效果比较差.针对这一问题运用split-and-conquer加向前选择法对非参数可加模型进行研究，以解决传统方法在处理超高维数据时耗时过长的问题.

1 非参数可加模型

Stone[9]首次提出非参数可加模型，具体的表达式为

(1)

其中，X表示解释变量，Xij表示向量Xi的第j个变量，Y表示被解释变量，(Yi,Xi),i=1,...,n与(Y,X)独立同分布.μ在这里是常数，作为截距项.εi是一个随机变量，其均值为0，方差为σ2.fj(j=1,…,p)表示函数项.当E(Xij)=0,Var(Xij)=1,E(Yi)=0,Var(Yi)=1时，常数项变为0，即μ=0.本文假设函数满足Efj(Xj)=0,1≤j≤p使得函数展开时具有唯一性，即使得被解释变量的均值为0.我们定义指标集P1={1,2,…,p},|P1|=p=pn，使得fj(Xj)≠0时的变量为相关联的变量，与之对应的集合为M0={j:Efj(Xj)2>0}，那么此时得到的稀疏模型就为p0=|M0|.

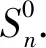
(2)

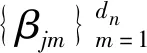
2 数据处理方法

面对大量的高维数据，尤其当数据维数高于样本量的时，进行变量选择迭代次数很大，会浪费很长的时间.而split-and-conquer方法进行变量选择前的数据处理可以解决耗时长的问题.

2.1 spilt-and-conquer方法

Chen提出的split-and-conquer方法[10]，不仅能够很好的去除错误模型选择带来的伪相关，而且可以极大地降低计算时间.计算机产生的时间复杂度正比于O(na,pb),a>1,b≥0.

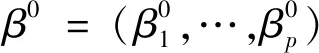
(3)

相应的惩罚估计为:

(4)

其中ρ(β;λk)训练参数λk的惩罚函数，可参见文献[11].当数据量比较大的时候，此方法不仅能够选择出关联特征，还能很大程度上节省时间.

2.2 非参数向前选择法

秦玲晔[12]提出了非参数向前选择法.向前选择方法一般用于参数回归中，将其用到非参数回归中，运用残差平方和进行选择，得到使残差平方和最小的变量.筛选的变量集合为：

具体步骤为：

1)设t1=0,S0=0.

2)进行迭代.当t1次迭代，St1-1和P1﹨St1-1中的各个元素为备选模型Mj,t1-1=St1-1∪{j}，计算每个j值的RSSMj,t1-1，选择出RSS最小时的j值记为at1=arg minj∈P1﹨St1-1RSSMj,t1 - 1,迭代得到St1-1∪{at1}.

由于非参数向前选择法比较复杂，会消耗很长时间，所以本文通过设置残差平方和的大小来控制迭代.设迭代次数为D0时可以停止,记BIC准则为：

(5)

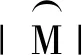
非参数向前选择法具有变量选择一致性的特点.

2.3 评价标准

本文考虑真正例、假正例、R23个指标来衡量模型的好坏.

真正例表示预测值和真实值同为1，而假正例表示真实值为0，预测值为1的情况，在文章中我们希望真正例越大越好，而尽量避免假正例的存在.

平均模型大小可以看做变量选择模型好坏的评价指标，可通过计算样本的R2，即

(6)

当R2越大，则表示模型的拟合效果越好.

3 数据模拟

考虑模型1：Y=g1(X)+g2(X)+g3(X)+g4(X)+ε

其中g1(X)=-sin(2x)，g2(X)=x2-25/12，g3(X)=x，

g4(X)=exp(-x)-2/5×sin(2.5)，X～U(-2.5,2.5),ε～N(0,1).

定义信噪比为3.可得到函数与非参数可加模型的拟合结果图如图1所示.

图1中是通过变量选择后前 4个得出来的图，虚线是函数的真实值，实线是预测值，2条外部的实线表示预测值的置信区间.图1、2中横坐标表示自变量，纵坐标表示预测值.从模拟图c中可以明显地看出来，当预测的函数比较简单，呈一条直线时，预测效果较好，预测曲线与真实曲线都比较接近；当预测的函数为一条简单曲线，如拟合图d，预测值与真实值会在曲线的地方发生较小偏离；从拟合图a和b中可以看出，非参数向前选择法在预测曲线的拐角处时会发生较大偏离，预测效果较差.总的来说，随着真实曲线的曲度不同，非参数向前选择法预测的效果稍有差别，但总体预测效果较好.

图2中预测曲线与真实曲线都比较接近.当曲线比较简单时，模型拟合的比较好；当曲线比较复杂时，模型模拟的稍微差一点.但是总的来说，选择出的变量还是与真实曲线的走势一致，如模拟图f1，当真实曲线发生较多拐弯，虽然在拐弯处发生了偏离，但预测曲线仍可以适应其正确的走势.根据模拟1和2，得出模型在时间和预测准确度方面的结果.为了对比，加入split-and-conquer(SAC)方法对数据处理，以验证是否在保持模型准确性的同时，能节省时间.非参数向前选择法，文献[12]给出了详细的解释.本节得出的数据结果，如表1所示.

表1 模拟数据效果对比

表1中，模拟1的数据通过非参数向前选择法得到的正确率为0.936，消耗时间为 12.12 min.通过 SAC 方法处理数据后，再使用非参数向前选择法得到的准确率为 0.923，消耗时长为4.31 min.结果表明，数据通过SAC方法处理后准确率减小了，但是影响程度不大.从消耗时长的角度来看，有很好的效果，节省了 7.81 min；模拟 2的数据通过非参数向前选择法得到的正确率为 0.797，消耗时长为 15.68 min.通过SAC方法处理数据后，再使用非参数向前选择法得到的准确率为 0.824，消耗时长为 3.96 min.结果表明，数据通过SAC方法处理后准确率增加了，但是影响程度也不大，而从消耗时长来看，节省了 11.72 min.总之，数据进行SAC处理后，通过非参数向前选择方法进行变量选择，对模型的准确率影响不大，能保证处理前后结果的一致性，然而对数据进行SAC方法处理后，能较好地节省时间.

4 结语

变量选择是解决大数据的一种方法，但是有效地处理高维数据有一定难度.本文针对这一问题提出了一种新的方法进行变量选择.首先使用split-and-conquer方法将数据进行拆分，然后使用B样条函数逼近的非参数向前选择法进行研究.模拟实验表明，基于split-and-conquer的非参数向前选择法可以将变量选择出来，并且节省了大量时间.