Benard对流问题五模类Lorenz方程组混沌行为的数值模拟
2019-12-03王贺元
王贺元, 张 颖
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
0 引 言
Lorenz方程是将满足一定边界条件的Navier-Stokes方程和热传导方程进行傅立叶展开后截断而产生的[1-2]。其实际背景来源于简化的大气对流模型,两平行板间充满流体从下板加热,热量从下至上传递,当温度比较低时,热量通过热传导方式传递,流体不发生运动。当温度增高时,液体就要发生对流,当温度继续升高时,液体会发生对流。在热压力条件下不可压缩的流体运动可以被描述为如下偏微分方程组:

(1)
其中u=u(x,y,z)为流体的速度场,T=T(x,y,z)为流体的温度场,在这个方程中式中常数g,ε,v和k分别表示重力加速度,热膨胀系数,运动粘性系数和热传导系数,ΔT为两板间的温度差,p为流体的压力场,在边界上u=u(x,y,z)。
1 竖直截面上的二维对流问题
仅考虑竖直截面上二维流动问题,引入函数τ(x,z,t),它的梯度为速度场,同时引入θ(x,z,t)为流体的温度场,并且在静态条件下θ(x,z,t)=T(x,z,t)-T0,这里的T0在两板间呈线性递减,假定流体不可压缩,则方程(1)可表示为如下形式:
函数ψ(x,z,t)和θ(x,z,t)在边界上满足
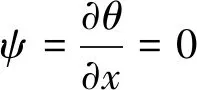
(4)
对ψ(x,z,t)和θ(x,z,t)傅立叶展开成如下形式:
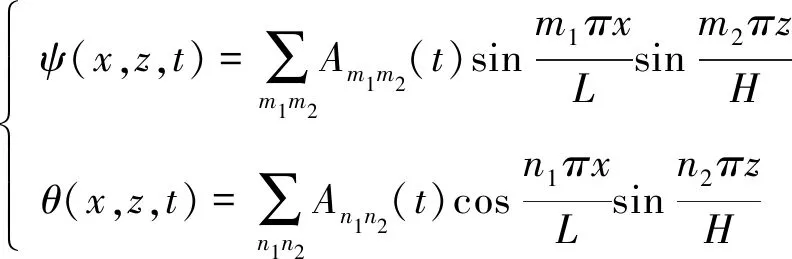
(5)
在具体截断过程中,将m1m2,n1,n2,赋予具体的值,使得ψ(x,z,t)和θ(x,z,t)成为具体的式子,然后将ψ(x,z,t)和θ(x,z,t)代入式(2)~式(4)中,经过复杂计算通过待定系数得到截断方程。
依照上述截断的方法,在截取五模类Lorenz方程组时,将ψ(x,z,t)和θ(x,z,t)展式设为如下形式:

(6)
其中x1相当于通项中的A1,x2相当于通项中的A2,x3相当于通项中的A11,x4相当于通项中的A12,x5相当于通项中的B02,C1,C2为常系数。
经运算得
把上述各式代入式(2)和式(3)中,再利用边界条件(4)经整理并根据物理意义取定其中的参数得到如下五模类Lorenz方程组:
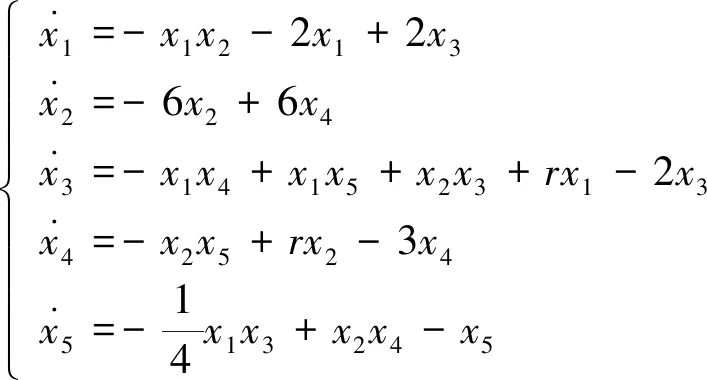
(14)
其中r与温度有关,称为Rayleigh数。
2 数值模拟
上述非线性方程组(14)具有复杂的动力学行为,下面我们来数值模拟当参数r变化时方程组的动力学行为如下(取坐标为x2,x4,x5):

图1 r=48.3 绕一点旋转Fig.1 r=48.3 Rotate about a point
1) 图1表示当r=48.3时方程组的解轨线不断绕一点(平衡点)旋转,且越转越密,此时系统稳定,图2(r=69.2)为轨线绕一点旋转的另外一种形态,轨线不断增多且向一起靠拢;图3表示当r=71.4时,系统发生了Hopf分岔[3-6],出现了极限环;图4所示当r=72.3时由原先的绕一点旋转变为绕两点旋转。
2) 图5(r=74)、图6(r=76)为系统不断分岔出一些新轨线,新轨线继续绕两点旋转,即发生了混沌现象,出现奇怪吸引子[6]。

图2 r=69.2轨线聚集Fig.2 r=69.2 Rail line to gather
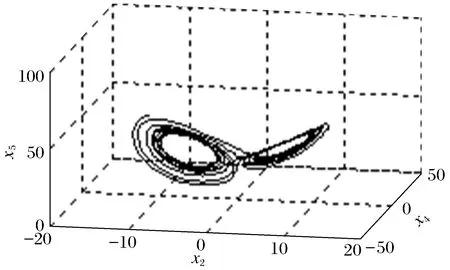
图4 r=72.3绕2点旋转Fig.4 r=72.3 Rotation about two points

图5 r=74奇怪吸引子 Fig.5 r=74 Strange attractor
3) 图7~图11分别给出了系统的分岔图、最大李雅普诺夫指数、庞加莱截面、返回映射和功率谱,它们展现了系统混沌行为的普适特征。

图6 r=76奇怪吸引子Fig.6 r=76 Strange attractor

图7 分岔图Fig.7 Bifurcation diagram
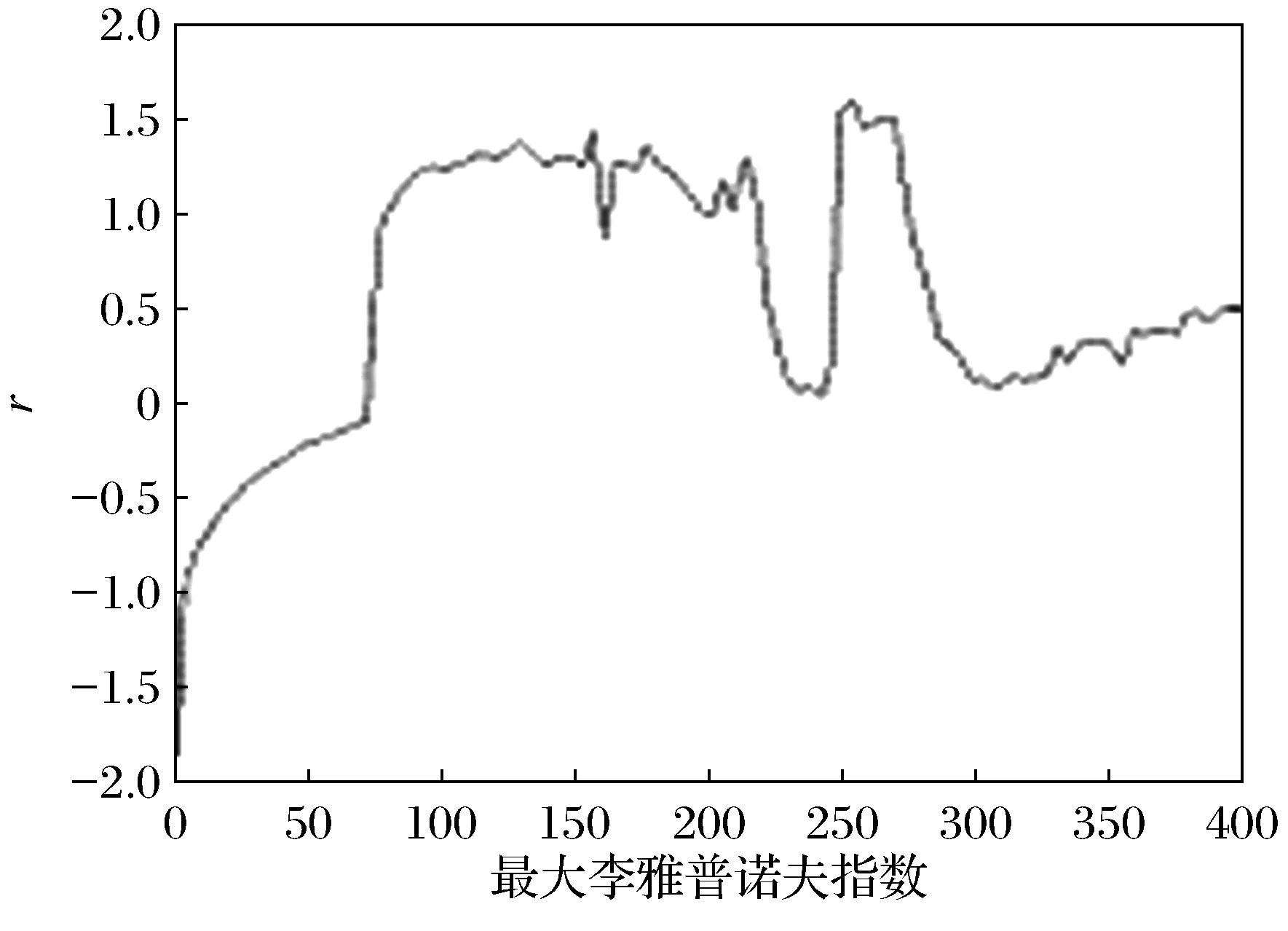
图8 最大李雅普诺夫指数Fig.8 The largest lyapunov index

图9 r=84.65庞加莱截面Fig.9 r=84.65 Poincare spectru
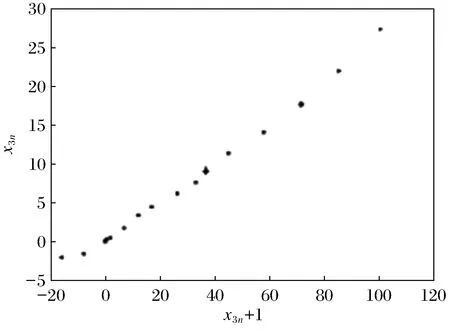
图10 r=84.65返回映射Fig.10 r=84.65 Return to the map

图11 r=84.65功率谱Fig.11 r=84.65 Power spectrum
3 结 论
本文介绍了Lorenz方程截断的基本方法,对Navier-Stokes方程与热传导方程中的速度场和温度场等变量进行二维傅立叶展开,经过复杂运算最后得到新五模方程组,并对其动力学行为进行了数值模拟。