理想弹性体体积模量二维与三维不一致原因分析

黄小华, 朱嘉正, 金艳丽

(广西大学 土木建筑工程学院, 南宁 530004)

0 引 言

弹性模量是衡量材料受力时产生弹性变形难易程度的性能指标,是弹性材料最基本的力学特性参数。相应于不同的变形,有不同的称谓。例如,拉伸变形时的拉伸模量(E)、剪切变形时的剪切模量(G)、体积变形时的体积模量(K)等。对于各向同性线弹性材料,这些弹性模量中真正独立的仅有2个,它们之间可通过转换公式得到。在三维应力空间(或状态)中,体积模量通常定义为弹性微元体平均应力(即该微元体3个主应力的平均值)与体应变的比值。对于各向同性线弹性材料,它常被表达为[1-3]:

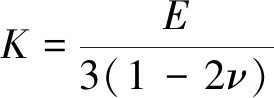
(1)

式中,ν为泊松比。

然而在二维应力空间中,体积模量有了新的表达,如Torquato[4],Madenci[5],Bobaru[6],Chen[7],Kachanov[8],Zhang[9-10],Van Le[11]等人给出了二维平面应力状态下的体积模量:

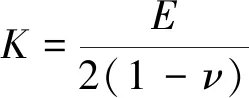
(2)

Torquato[4],Bobaru[6],Zhang[9-10],Van Le[11]等人也给出了二维平面应变状态下的体积模量:

(3)

更有甚者,Torquato[4]和Ostoja-Starzewski[12]还在二维应力空间中建立了一套弹性模量转换公式,如表1所示,它是一套完全异于三维应力空间的全新转换公式。二维应力空间本是从三维应力空间简化而来,是三维应力空间的特殊情形,理应具有与三维应力空间完全相同的体积模量,以及完全相同的弹性模量转换公式,但缘何它又能自成系统,采用全新的体积模量表达式,即式(2)或式(3),以及全新的转换公式。在二维应力空间问题中,体积模量到底该采用上述何种表达形式?抑或在二维应力空间中,我们仍采用式(2)或式(3)表达的体积模量,那我们应该注意些什么?针对这些问题,本文从线弹性本构理论出发,找出体积模量随应力空间维数变化的原因,从而提出使其在各维应力空间保持一致的处理办法。

表1 二维应力空间中弹性模量的表达及其转换[12]Table 1 Elastic modulus in 2D space expressed in 3D Moduli and its interelations

1 体积模量随应力空间维数变化的原因

1.1 三维应力状态的体积模量

各向同性线弹性体的三维本构关系为:

σij=λεkkδij+2μεij

(4)

或

(5)

式(4)和式(5)中,σij和εij分别为应力张量的分量和应变张量的分量,根据爱因斯坦求和约定,其下标i和j表示在其取值范围内遍历,通常采用拉丁字母i、j和k等来表示它在三维空间,即在(1,2,3)中遍历取值,而采用希腊字母α、β等来表示二维空间,即在(1,2)中遍历取值。符号λ和μ为拉密常数,

(6)

由体积模量的三维定义及式(4)可得

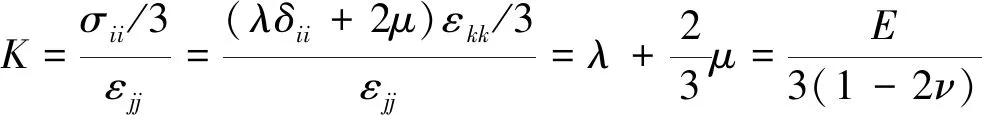
(7)

由式(4)和式(7)可得,三维应力状态下,各向同性线弹性体的本构关系进一步表示为

(8)

1.2 平面应力状态的体积模量

二维平面应力状态认为σ3i=0,(i=1,2,3),因此由式(5)可得正应变和正应力分别为

通常ε33≠0,倘若仅关注面内的应力和变形,将二维体积模量定义为弹性微元体的面内平均应力(即该点面内主应力的平均值)与面内体应变的比值,即

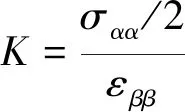
(11)

将式(9)代入式(11)得

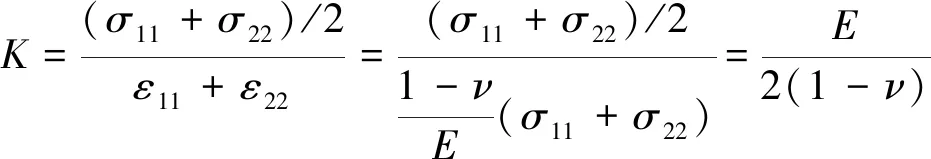
(12)

由式(10)和式(12)可得以体积模量表示的平面应力状态下应力与应变关系为:

σαβ=(K-μ)εηηδαβ+2μεαβ

(13)

1.3 平面应变状态的体积模量

二维平面应变状态认为ε3i=0,(i=1,2,3),因此由式(4)可得正应力为

(14)

通常σ33≠0,与前面介绍的二维平面应力状态相似,这里也只关注面内的应力和变形,采用式(11)定义的体积模量,则将式(14)代入式(11)得

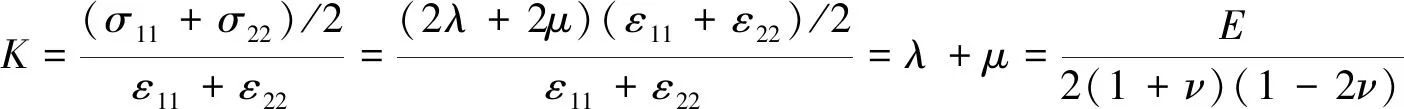
(15)

由式(14)和式(15)可得以体积模量表示的在平面应变状态下应力与应变关系式:

σαβ=(K-μ)εηηδαβ+2μεαβ

(16)

不难发现,式(13)和式(16)完全一样,即二维应力状态下,无论是平面应变状态还是平面应力状态,以体积模量表示的应力与应变关系式是一样的,但值得注意的是这两个式子中的K的表达式却不同。此外,式(2)与式(12)完全相同,式(3)与式(15)也完全相同,这表明Torquato[4]、Madenci[5]、Bobaru[6]和Ostoja-Starzewski[12]等在研究二维平面问题时,都将研究重点放在“理想的二维平面”内线弹性体的应力和变形上,因此他们全新定义了二维平面问题体积模量的表达形式,正是这种人为的全新定义导致了体积模量的二维形式与三维形式发生显著的变化。但值得注意的是,这种仅关注平面内应力和变形的体积模量的定义形式并不能等价地认为他们彻底忽视了平面外的应力和应变,因为如果彻底忽视平面外的应力和应变,则无论平面应力状态还是平面应变状态,都应同时有σ3i=0,ε3i=0,(i=1,2,3),显然,这种应力状态违背了平面应力或者平面应变的定义,倘若认为这种应力状态存在,那么这种应力状态既可以认为是平面应力状态,也可以认为是平面应变状态,那么由它代入式(11)导出的体积模量,也既应该是平面应力的体积模量,也应该是平面应变的体积模量,如此,平面应力和平面应变的体积模量将具有完全相同的表达形式,这明显和前面指出的平面应力和平面应变的体积模量分别是式(2)和式(3)的事实相矛盾。

上述分析也表明若要保证体积模量在各维应力空间保持一致的表达形式,唯一的办法是各维应力空间的体积模量必须采用相同的定义,即二维应力空间的体积模量不能进行“全新定义”,而必须也采用式(7)的定义形式。也就是完全按照三维应力空间的情形进行计算,计算过程中,根据二维应力状态的特殊性进行相应的简化。

当然,在二维应力空间中,如果体积模量仍坚持采用式(2)或式(3)的表达形式,此时,必须清楚此“所谓的体积模量”实质上是一种人为定义的新的弹性模量,它并不是通常所说的“体积模量”,根据它的定义形式,建议将其命名为“面内体积模量”或者“面积模量”更恰当,因为它描述的是“弹性微元体的面内平均应力(即该点面内主应力的平均值)与面内体应变的比值”。

2 结 论

1) 针对体积模量的二维表达形式与其三维形式存在显著不同这一问题,从线弹性本构理论出发,找出了体积模量随应力空间维数变化的原因,乃是人们为了将研究重点放在线弹性体“二维面内”的应力和变形上,而全新定义了体积模量的表达形式。严格来说,这种“体积模量”是一种新的弹性模量,它并不是我们通常所说的“体积模量”,根据它的定义,建议将其命名为“面内体积模量”或者“面积模量”更合理,从而更好地与通常所说的体积模量相区分。值得指出的是,这种仅关注平面内应力和变形的体积模量的定义形式实质上并没有彻底忽视平面外的应力和应变,这也就是为什么二维体积模量出现平面应力状态和平面应变状态两种不同形式的原因。

2) 确保体积模量在各维应力空间保持一致,唯一的办法是各维应力空间的体积模量必须采用相同的定义,即二维应力空间的体积模量不能采用“全新定义”,而必须完全按照三维应力空间的情况进行计算,计算过程中,根据二维应力状态的特殊性进行相应的简化,如此,无论是二维平面应力状态还是二维平面应变状态,其体积模量都将与三维保持一致。