模量面内变化的梯度功能弹性薄层接触应力分析

2019-12-02金明生董晓星王礼明计时鸣

中国机械工程 2019年22期

金明生康杰董晓星王礼明计时鸣

浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点实验室，杭州，310023

0 引言

现有化学机械抛光、流体抛光等传统或新兴超精密加工技术在取得相关技术突破的同时，也存在不可忽视的问题，其中材料均匀去除问题就需要解决。由Preston方程可知，接触应力不均以及相对速度分布的非均匀所引起的材料去除非均匀是加工平坦度差的重要根源。LIN等[1]、吕玉山等[2]与杨争雄等[3]均指出了应力分布对材料均匀去除的影响。同时，复合材料在抛光领域的应用日渐增长。白林山等[4]采用均相沉淀法制备了SiO2/CeO2复合磨料，改善了蓝宝石晶片的表面质量。计时鸣等[5-7]提出了一种基于软固结磨粒气压砂轮的光整加工新方法，研究了气压砂轮软固结磨粒群的内部磨粒拓扑结构对加工材料去除率的影响。

梯度功能材料是一种新型复合材料，通过连续改变两种(或多种)材料的组成和结构，使其界面消失导致材料的性能随着材料的组成和结构的变化而缓慢变化。滕兆春等[8]讨论了弹性地基模量和梯度指数对功能梯度材料Timoshenko梁自振频率的影响。舒小平[9]对功能梯度压电涂层的热效应进行分析，指出增加涂层层数可显著减小相邻层层间应力的突变幅度。贺丹等[10-11]基于新修正偶应力理论，建立了微尺度平面正交各向异性功能梯度梁模型，并分析了弯曲和振动问题。CHOI[12]针对厚度方向上剪切模量呈指数变化的具有一定厚度的梯度层，研究了平冲头加载功能梯度层的摩擦滑动接触力学，在平面弹性方程和Fourier积分变换技术的基础上，提出了一种求解未知接触压力的Cauchy型第二类奇异积分方程。SU等[13-16]分析了功能梯度压电层状半空间在不同形貌的刚性冲头下的接触问题。CHEN等[17]提出并研究了具有线性梯度层的齐次半空间与刚性凸模之间的接触模型。LIU等[18]采用线性多层模型对剪切模量为任意函数变化的功能梯度层进行了建模，应用Hankel积分变换技术和传递矩阵法，将双接触问题转化为耦合奇异系统来考虑刚性圆柱形和刚性球头压入的功能梯度层的轴对称双接触问题。孙喜阁[19]对功能梯度材料的制备及无摩擦接触进行了模拟分析。

关于材料特性沿厚度方向变化的梯度功能材料的接触问题已经有了充分的研究与讨论，但梯度在面内分布的研究较少。彭旭龙[20]对任意梯度变化的功能梯度材料的相关动静态力学问题提出了一种积分方程解法。陈伟球等[21]利用辛弹性力学解法分析了沿长度方向弹性模量为指数函数变化的矩形域平面弹性问题。DAG[22]采用展开配置技术以及Jacobi多项式对奇异积分方程进行数值求解，研究了剪切模量和摩擦因数都是面内梯度变化函数的半空间接触问题。这些学者的研究对梯度功能材料的应用有着指导作用，但接触问题的解析过程较复杂繁琐。

本文提出一种基于梯度功能研抛盘的加工新方法，研究了模量面内变化的梯度功能弹性薄层接触应力问题，旨在实现接触应力面内梯度变化以及用一种简单的解析方法得到梯度功能研抛盘接触应力的预测方程。

1 梯度功能研抛盘加工原理

梯度功能研抛盘加工原理如图1所示。具有梯度分布的弹性层由磨粒与黏结剂按不同体积比固结而形成，在面内呈现梯度分布，黏覆在刚性基底上，随基底一起旋转。负压配模组件通过负压吸附工件并夹持在配模上，以一定的位移下压量与梯度弹性层接触，进行研抛。

图1 梯度功能研抛盘加工原理Fig.1 Processing principle of functionally graded lapping and polishing plate

梯度功能研抛盘应用了“软固结磨粒”理念，磨粒的存在形式不同于游离磨粒的自由移动，亦不同于嵌于刚性基体上的固结磨粒与工件表面的刚性接触，磨粒与弹性黏结剂混合形成的弹性体复合材料黏覆在刚性基体表面，磨粒各个方向受到黏结剂的弹性支撑，在受轻载荷情况下可以局部微动而不脱落。根据Preston方程M=KPV(其中，K在确定环境下是个定量，材料去除量M取决于工件接触面所受的正应力P与相对磨粒的线速度V，保证P与V乘积为常数)，在弹性层面内的径向，通过改变磨粒和黏结剂的体积配比实现弹性层在径向呈现弹性模量梯度分布，可有效提高材料的去除均匀性。

梯度功能研抛盘加工新方法的先进性体现于：①研抛盘采用软固结磨粒方法，与固结磨粒抛光方法相比，可有效减轻固结磨粒对工件表面的深划痕问题，与游离磨粒抛光方法相比，可提供磨粒稳定的支撑，材料去除效果更有效，去除过程更平稳；②引入梯度功能理念，改变研抛盘面内材料特性的分布，实现工件接触面的接触应力梯度分布，有效提高材料的去除均匀性。

2 接触应力分析与仿真

2.1 接触模型及控制方程

将此梯度功能研抛盘的接触情况简化为图2所示的接触模型截面并进行分析，忽略体力作用。图2中，均匀刚性基体上黏覆厚度为h的梯度弹性层，在外力F的作用下，宽度为a的平底刚性体与梯度弹性层发生法向接触，在不考虑刚性体自重的情况下，刚性体下压量为δ。

图2 梯度弹性层与平底刚性体的无摩擦法向接触Fig.2 Frictionless contact model of graded elastic layer and flat bottom rigid body

梯度弹性层泊松比为常数，且弹性模量在径向按照如下形式变化：

E(y)=E0+E*y

(1)

式中，E(y)为沿径向Y坐标系上某一点y的弹性模量；E0为梯度弹性层在y=0点处的弹性模量；E*表示梯度弹性层在径向的弹性模量E(y)变化的非均匀性程度，E*>0表示弹性模量沿径向正向线性递增，E*<0表示弹性模量沿径向正向线性递减。

接触问题分析基本方程[23]如下。

平衡方程：

(2)

式中，σx、σy、σz为各个轴向的正压力；τyx、τzx、τzy、τxy、τxz、τyz为作用在各个面上的切应力，且有τyx=τxy，τzx=τxz，τzy=τyz。

几何方程：

(3)

式中，εx、εy、εz、γyz、γzx、γxy为应变；u，v，w为各个轴向的位移分量。

物理方程：

(4)

式中，E为材料的弹性模量；υ为材料的泊松比。

假设刚性体与梯度弹性层做无摩擦接触，此时接触区内只有正压力存在，故接触必须满足如下边界条件：

τyz=τzx=τxy=0y∈(-∞,+∞)

(5)

σz=0y∈(-∞,0)∪(a,+∞)

(6)

(7)

同时在z=h的梯度弹性层与刚性基底的固结交界面上，存在边界条件如下：

w|z=h=0y∈(-∞,+∞)

(8)

v|z=h=0y∈(-∞,+∞)

(9)

根据Preston方程，本文旨在讨论刚性体与梯度弹性层接触区竖直方向的法向应力。在此引入补偿函数H(z)来取代εx与εy对σz的影响，拟定梯度弹性层在竖直方向的位移如下：

(10)

在拟定的位移公式中，H(z)仅为z的函数，且必须满足H(0)=0与H(h)=0，其具体形式将在后面的讨论中确定。

根据式(3)、式(4)与式(1)得

(11)

刚性体接触面的接触应力分布P(y)为

(12)

2.2 梯度功能研抛盘有限元接触模型

图3 试件与研抛盘有限元接触模型Fig.3 Finite element contact model between the test piece and lapping and polishing plate

工件与研抛盘表面接触的压力分布受多重因素影响，包括下压量、研抛盘材质、研抛盘厚度等，并且弹性层在接触受力过程中产生弹性变形。在此，应用ANSYS Workbench对研抛盘进行建模和网格划分，如图3所示。模型中所用材料参数和几何尺寸如表1所示。传统抛光过程中，工件边缘会出现接触应力突变，造成边缘过抛现象，本研究应用工件配模[24]技术来缓解工件边缘现象。工件选用铜片试件，在模型中，假设各实体表面紧密接触，上下表面均为平面。在Y轴方向，取试件与研抛盘接触面的中线为应力取值线。

表1 材料参数和几何尺寸Tab.1 Material parameters and geometric dimensions

2.3 仿真结果与分析

通过试件配模来缓解边缘效应的原理是将接触区域的边缘转移至有效去除范围之外，从而减缓试件边缘去除量过大的现象。在试件有配模和无配模两种情况下，施加0.2 mm的下压量，试件边缘效应现象减弱情况如图4所示。

图4 配模对应力边缘效应的影响Fig.4 Influence of matching module on stress edge effect

由图4可以看出，在试件无配模的情况下，试件边缘附近接触应力突变明显；在试件有配模的情况下，边缘应力突变减缓明显，且有无配模对试件接触区中心部位接触应力的大小无影响。

保持模型尺寸参数不变的情况下，将接触区沿Y轴宽度方向等分成同心环，赋予弹性层上各个同心环不同的弹性模量，实现弹性层沿径向梯度分布，分布情况如表2所示。

在无梯度分布和3梯度分布两种情况下，对试件接触表面应力进行仿真，对比结果如图5所示。分析图5可得,无梯度变化的研抛盘与试件接触面的应力数值大致相等，呈线性梯度分布的研抛盘与试件接触面的应力分布也呈现线性分布趋势，应力分布规律与理论分析相符。

表2 研抛盘梯度分布仿真参数Tab.2 Gradient distribution simulation parameters of lapping and polishing plate

注：Wi表示研抛盘的梯度数，如W3表示3梯度。

(a) 无梯度

(b) 3梯度图5 试件接触表面应力云图Fig.5 Stress map of test piece contact surface

图6为下压量δ=0.2 mm时，两种厚度下试件与梯度弹性层的接触应力。分析可得：①3梯度弹性层下接触应力由于梯度跨度相对较大造成了相邻梯度环界面之间的应力突变较大；②随着梯度环数的增加，各梯度界面应力过度更平缓，且不同梯度分布下，应力曲线变化幅度保持在10%以内；③应力突变界面会随着梯度环数增加或梯度变化跨度减小而趋于消失。

(a) h=5 mm

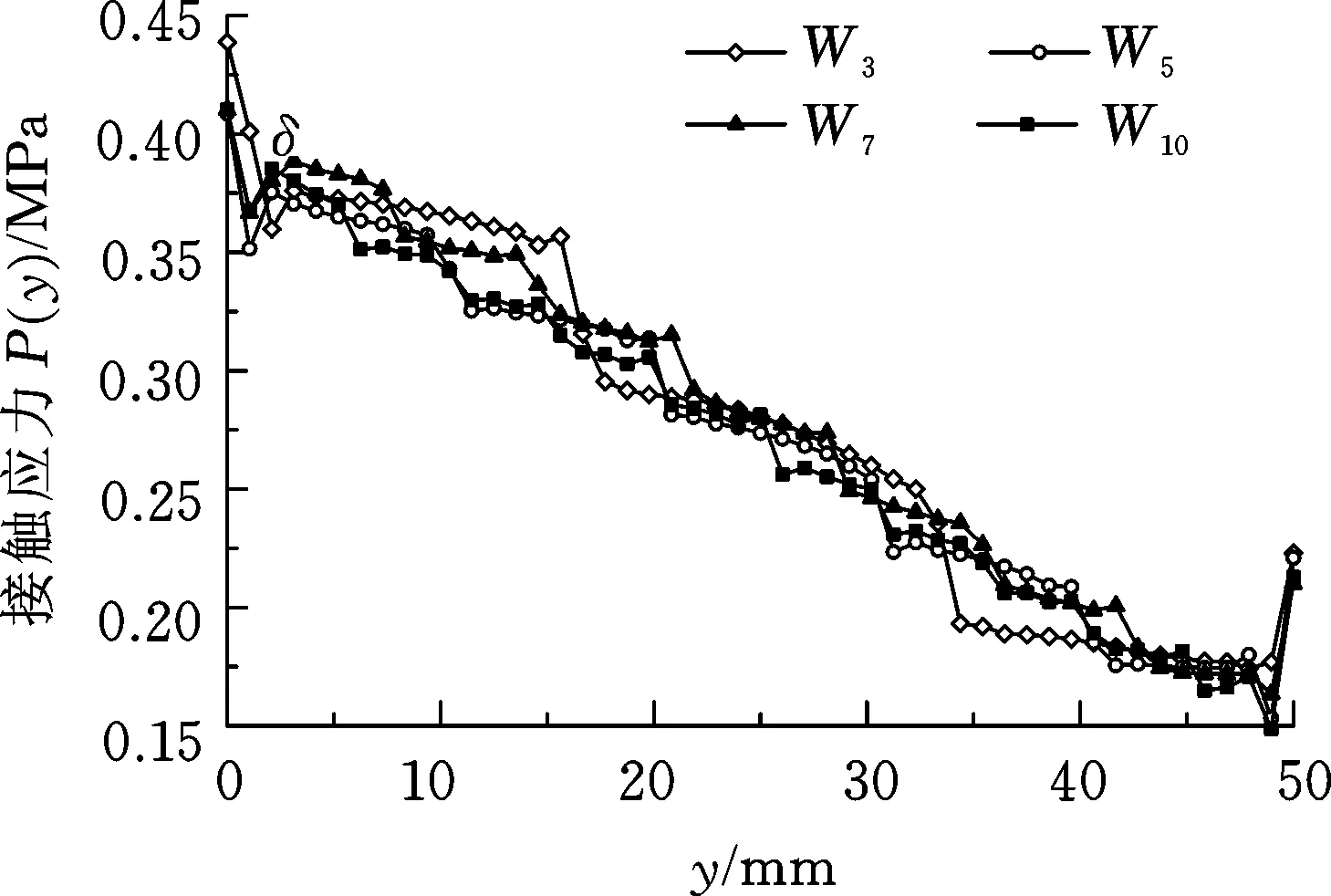
(b) h=10 mm图6 不同厚度梯度弹性层接触应力对比Fig.6 Comparisons of contact stress of different thickness graded elastic layers

综合以上结论以及考虑制作多环梯度弹性层的难度，下文均取5梯度进行讨论。

(13)

综合可得P(y)为

(14)

通过数值计算与仿真分析的对比，可以确定N的取值范围。

图7将仿真与无补偿函数H(z)下的控制方程进行了对比。弹性层厚度h=5 mm的5梯度研抛盘在下压量δ=0.2 mm下，应力方程计算出的接触应力相对于仿真结果偏大，因此可以明确N的取值范围为[0,1]。在取值范围内，对式(14)取值拟合，鉴于抛光对去除量的要求不大，对表面质量要求严格，且抛光过程中下压量不宜过大，取δ/h∈[0.01,0.06]，结果如图8所示。

图7 H(z)对接触应力预测的影响Fig.7 Influence of H(z) on contact stress prediction

(a) δ/h∈[0.01,0.03]

(b) δ/h∈(0.03,0.06]图8 不同δ/h下的数值拟合Fig.8 Numerical fitting curves under different δ/h

图8a和图8b分别为δ/h∈[0.01,0.03]和δ/h∈(0.03,0.06]的拟合匹配结果。结果表明在相同δ/h下，改变厚度和下压量对接触应力的一致性影响不大，同时方程拟合误差也保证在10%以内。

将图8对式(14)N的取值提取出来，进行函数N(δ/h)的拟合，如图9所示。由图9可得，确定了研抛盘的梯度分布后，总有唯一的一条N(δ/h)曲线可以代入式(14)，从而求出接触应力的分布，为后期材料的加工提供参考。

图9 函数N(δ/h)的拟合曲线Fig.9 Fitting curve of function N(δ/h)

3 试验与讨论

由仿真结果可知，面内梯度功能研抛盘与工件接触可有效实现工件接触应力梯度分布。本节通过搭建梯度功能研抛盘加工平台进行试验，验证接触应力的分布情况。

3.1 梯度功能研抛盘加工系统

图10为梯度功能研抛盘加工系统主体构成图，该系统在传统平面光整加工基础上对工件添加了配模，可有效减弱边缘效应，同时，引入梯度功能理念，实现工件接触表面的接触应力梯度分布，可更大程度地实现工件表面的均匀去除。

图10 梯度功能研抛盘加工系统Fig.10 Processing system of functionally graded lapping and polishing plate

负压发生器为负压配模组件提供稳定的吸附力以固定工件，抛光机可以实现50～1 000 r/min的无级调速，用3M瞬干胶将抛光机旋转盘基底与梯度功能研抛盘固结，控制面板控制工件的水平位置和下压量，PC机通过力传感器实时监测抛光过程中负载力的变化，反馈负载变化情况。

在进行工件下压的过程中，保证工件与研抛盘盘面的平行，实现工件与研抛盘接触面的同一形变量，确保结果的准确性。对工件施加一定的位移下压量，工件与盘面的接触面和工件载荷加载面的应力分布是相同的。同时，为了保证梯度研抛盘在工件以一定下压量作用下，接触面各处变形量相等，选择将传感器的位置布置在工件载荷加载面上，即工件上表面上。对应于梯度研抛盘的5个梯度环位置，在工件上布置传感器。传感器选用RFP系列电阻式薄膜压力传感器，传感器测试精度为0.1 N，转换成应力可达0.005 MPa。

3.2 接触应力结果

在制备梯度功能研抛盘时，将黏结剂与磨粒按照不同体积比配比混合固结。研抛盘上磨粒具备软固结特性，其中黏结剂必须具备一定的弹性与良好的流动性。综合以上特性，选择有机硅电子灌封胶作为黏结剂，白刚玉微粉作为磨粒。

取表2中5梯度研抛盘的梯度分布，按照一定的体积比进行固结[25]，如图11所示。

(a) 5梯度研抛盘

(b) 梯度弹性层微观图图11 梯度功能研抛盘固化效果Fig.11 Curing effect of functionally graded lapping and polishing plate

研抛盘分为厚度5 mm和10 mm两种规格，对函数N(δ/h)取三组数值代入式(14)，得到3条应力曲线。试验对比结果如图12所示。由图12可知，应力函数可以很好地预测工件在梯度功能研抛盘上的接触应力分布，误差保持在10%以内，δ/h值越小拟合度越好，梯度弹性层厚度的影响越小。在δ/h∈[0.01，0.06]的范围内，应力预测方程可以很好地应用于梯度功能研抛盘的应力分析。